はじめに
昨年末 DEGwer さんの数え上げテクニック集 がとても勉強になる資料として話題になりました。その中の P. 9 の「4. 条件の言い換え」のところに、「必要条件を列挙したらそれが十分条件だった」がありました。
こないだの APC 001 E - Antennas on Tree がその面白い問題例と感じたのでメモします。
問題概要
N 頂点のツリーの頂点集合の部分集合 S のうち、「全頂点のどの 2 頂点 u, v を選んでも、S に含まれるとある頂点 w が存在して、u-w 間の距離と v-w 間の距離とが異なる」という性質を満たすような最小サイズのものを求めよ。
【制約】
・ 2 <= N <= 105
この手の問題を考えるときに、まずは列やスター (通称「うに」) のケースを考えてみるのはポイントなのかな...と思います。
列の場合は下図のように端っこの一方を選べばよいです (K = 1)。列以外のケースだと最低 2 個は必要になるので、なんとなくこれがコーナーケースになりそうな予感を念頭に置いておきます。

スター (うに) の場合は、下図のようにうにの先端を 1 個残して選ぶ必要があります。

このスターの場合をさらに推し進めて考えると以下のことが必要条件になるのがわかります:
どの頂点についてもその頂点を取り除いてできる部分木が m 個あるとすれば、そのうちの m-1 個の部分木からそれぞれ 1 個以上選ぶ必要がある
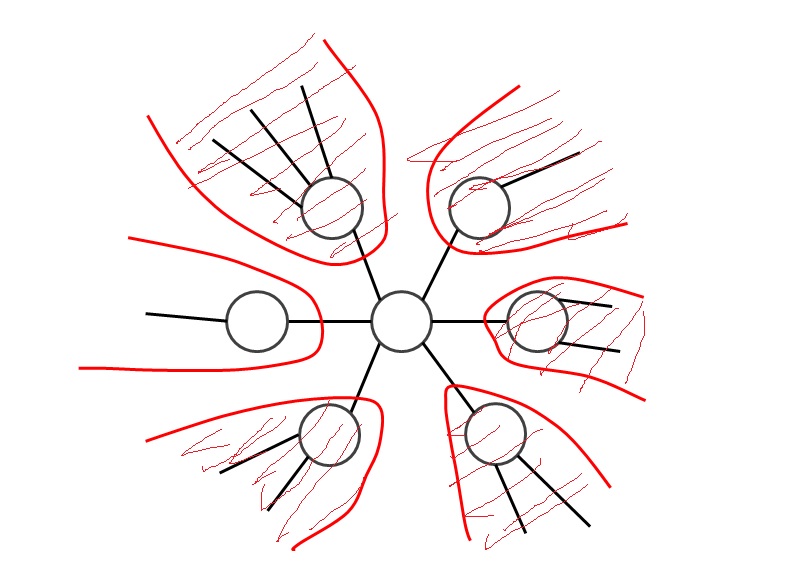
これが実は十分条件にもなっているようです。
次数 3 以上の頂点については、この条件を満たせば一意特定できるのはほぼ明らかです。次数 1, 2 の頂点についてが少し不安になりますが、よくよく考えると確かに一意特定可能になっています。
木 DP の枠組みに乗せることを考えてみます。部分木たちの親側に「選ばれた頂点」があるかどうかを分岐するのが面倒そうなので、次数が 3 以上の頂点を根にしてしまえばスッキリします。根の次数が 3 以上なら、どの部分木を考えているときも親側に必ず「選ばれた頂点」が存在することになります。そうすると
木 DP を営むときのどの部分木についても、その子供たちのなす m 個の部分木のうち m-1 個以上に選ばれた頂点があることが必要かつ十分
ということが言えます。ここまで来ればあとは自然に木DPができます。
#include <iostream> #include <vector> using namespace std; int N; vector<int> G[110000]; const int INF = 1 << 29; int rec(int v, int p) { int all = 0; int zero_num = 0; for (auto to : G[v]) { if (to == p) continue; int tmp = rec(to, v); all += tmp; if (tmp == 0) ++zero_num; } if (zero_num > 1) all += zero_num - 1; return all; } int main() { cin >> N; int r = -1; for (int i = 0; i < N - 1; ++i) { int a, b; cin >> a >> b; G[a].push_back(b); G[b].push_back(a); if (G[a].size() > 2) r = a; if (G[b].size() > 2) r = b; } if (r == -1) { cout << 1 << endl; return 0; } cout << rec(r, -1) << endl; }