AtCoder ABC 103 D - Islands War (水色, 400 点)

問題へのリンク

実は、こないだの RUPC 2018 で出てた (最後の部分のみほぼ同じ)

• AOJ 2873 - 検閲により置換

見た目は区間スケジューリング問題とは違うけど、実は区間スケジューリング問題 (こういうの双対問題と言ったりする)。双対性の知識がまったくなくても下に述べていることは理解はできるはず。

問題概要

個の区間 [ が与えられる。
区間を図のようにすべて串刺しにしたい。最小本数の串で区間を串刺しにせよ (図では 3 本)。

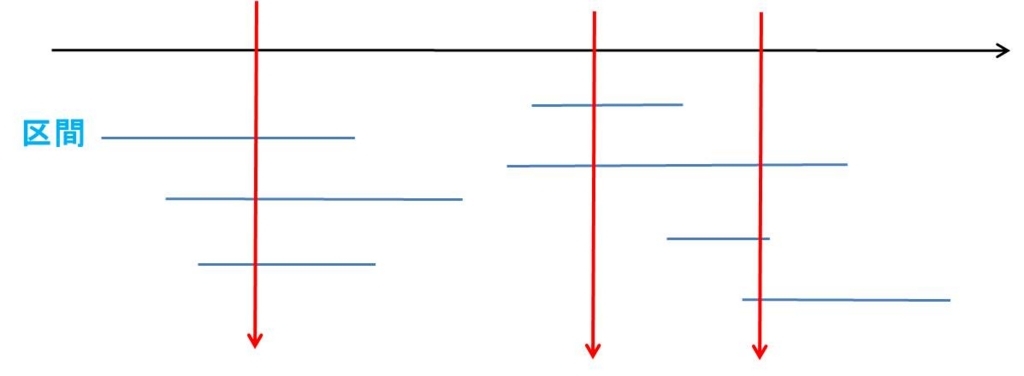
制約

• 
• <

解法

区間スケジューリング問題とは以下のような問題である:

---

個の区間が与えられ、どの 2 つの区間も時間帯を共有しないように最大個数の区間を選べ

---

蟻本の Greedy の章の最初にも載っている有名問題で、区間の終端でソートして Greedy にとっていけばよい。

実は今回の問題の答えは、区間スケジューリング問題の最適解と同じになる:

• まず区間スケジューリング問題の答えが 個だった場合、その 個は時間帯を共有しないので、それらを全部刺すには最低でも 本の串が必要である (弱双対性)

逆に 本の串があれば十分であることは、区間スケジューリング問題に対する貪欲法の動きを注意深く追うと理解することができる。具体的には、

• 区間スケジューリング問題で選ぶ 個の区間に対して、その右端から串を刺していけば、ちょうど 本の串ですべての区間を串刺しにできる (強双対性)

#include <iostream>
#include <vector>
#include <algorithm>
using namespace std;

int N, M;
typedef pair<int,int> pint;

vector<pint> A;
bool cmp(pint a, pint b) { return a.second < b.second; }

int main() {
    cin >> N >> M;
    A.resize(M);
    for (int i = 0; i < M; ++i) cin >> A[i].first >> A[i].second;
    sort(A.begin(), A.end(), cmp);
    int res = 0;
    int endtime = 0;
    for (int i = 0; i < M; ++i) {
        if (A[i].first >= endtime) {
            endtime = A[i].second;
            ++res;
        }
    }
    cout << res << endl;
}