素因数分解 & 重複組合せ
を勉強できる、すごく教育的問題だった!!!
問題概要
整数 が与えられる。
を満たす整数の組 () が何通りあるか、1000000007 で割った余りで求めよ。
制約
解法
素因数分解っぽいテーマの問題。こういうのは「まずは素数べきで考える」というのが 1 つの定石ではある。 を素数として
を満たす () が何通りあるかを考える。これは実は、
の指数に着目して
として、
を満たす 0 以上の整数 () が何通りあるかを数え上げる問題と考えることができる。
これは重複組合せ!!!!!
重複組合せは、「仕切りを使って考える」というのが 1 つの見方ではある。
個の玉と、
個の仕切りの並び替え方を数える問題
と考えることができる。
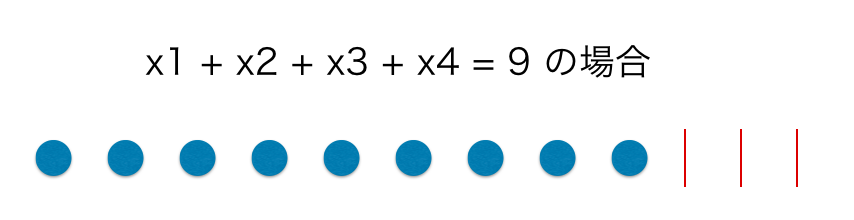
例えば のとき、上図のように、9 個の玉と 3 (= 4-1) 個の仕切りを並び替える問題だとみなすことができる。
の解と、「玉と仕切の並び替え」とが対応する例として、下図のような感じになる。
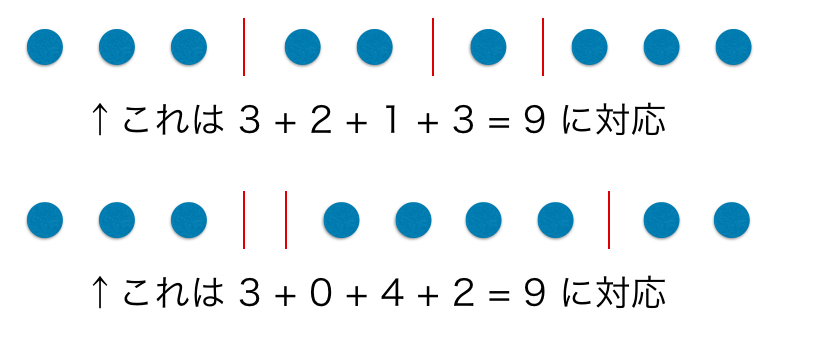
つまり場合の数は
である。二項係数の求め方については以前に書いた記事に書いてみた。
以上で、 が素数べきについての考察を終えたので、一般の合成数について考えることになるのだが、実は各素因子についてまったく独立に考えることができる。つまり、上記のことを各素因子ごとに独立に行って、得られた結果を掛け算していけば OK。
#include <iostream> #include <vector> using namespace std; vector<pair<long long, long long> > prime_factorize(long long n) { vector<pair<long long, long long> > res; for (long long p = 2; p * p <= n; ++p) { if (n % p != 0) continue; int num = 0; while (n % p == 0) { ++num; n /= p; } res.push_back(make_pair(p, num)); } if (n != 1) res.push_back(make_pair(n, 1)); return res; } const int MAX = 210000; const int MOD = 1000000007; long long fac[MAX], finv[MAX], inv[MAX]; void COMinit(){ fac[0] = fac[1] = 1; finv[0] = finv[1] = 1; inv[1] = 1; for(int i = 2; i < MAX; i++){ fac[i] = fac[i-1] * i % MOD; inv[i] = MOD - inv[MOD%i] * (MOD/i) % MOD; finv[i] = finv[i-1] * inv[i] % MOD; } } long long COM(int n, int k){ if(n < k) return 0; if (n < 0 || k < 0) return 0; return fac[n] * (finv[k] * finv[n-k] % MOD) % MOD; } int main() { int N, M; COMinit(); cin >> N >> M; auto vec = prime_factorize(M); long long res = 1; for (auto pa : vec) { int num = pa.second; long long tmp = COM(num+N-1, N-1); res = (res * tmp) % MOD; } cout << res << endl; }