Tenka1 2018 C - Align (緑色, 400 点)

今週のお題「わたしとバレンタインデー」

提出するまでが怖かった

問題へのリンク

問題概要

整数が N 個与えられます。
i 個目の整数は Ai です。 これらを好きな順に一列に並べるとき、隣り合う要素の差の合計の最大値を求めてください。

考えたこと

うおっ！！！
こんなシンプルな設定の問題が未出だったとは！！！！！！！

下手なことをやると間違えそう。パッと思い浮かぶのは (6 8 1 2 3) だったら、まず最大と最小を組み合わせてみたくなる

8, 1, 6, 2, 3

みたいに、一番大きいやつ、一番小さいやつ、二番目に大きいやつ、二番目に小さいやつ、、、とやっていくと良さそうに一見思える。しかしこれだと 17 で全然ダメ。本当の答えは 21。

よく考えると、最大から始めるか、最小から始めるかによっても変わる。最小から始めてみる:

1, 8, 2, 6, 3

しかしこれでも 20 でダメ。本当の答えは 21。

---

このあたりから、ちょっと真剣に考えないとダメだと悟る。とりあえずソートしておくのはよさそう。

あれこれ実験していると、N が偶数のときは

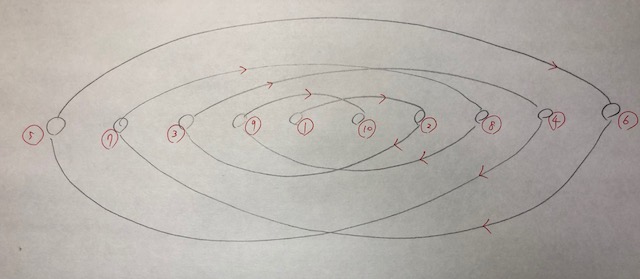
こんな風に並べるとよさそう。赤丸の 1 から 10 までを順に並べる感じ。こういう取り方をすると、1 回 1 回の差分がなるべく大きくなる感じ。

これが最大であることをちゃんと示してみようと思う (下に書くのは僕が本番中に考えていたことだったが、ちょっと見方が違ったより筋のいい証明が editorial にある)。

上図のやり方だと、左から数を a, b, c, d, ... として、b-a, c-b, d-c, ... がそれぞれ何回ずつ反映されているかを数えると

2, 4, 6, 8, 9, 8, 6, 4, 2

となっている。そしてよく考えてみると、例えば b-a を 2 回より大きくすることは絶対にできない (b-a のところをまたげるのは最大 2 本のみ) し、c-b を 4 回より大きくすることは絶対にできない (c-b のとろころをまたげるのは最大 2 本のみ)、、、という感じになっている。各区間をまたげる理論上最大回数をそれぞれ算出すると

2, 4, 6, 8, 9, 8, 6, 4, 2

となっていて、上のと一致する！！！以上のことから、上図のやり方が最大であることを確信が持てるに至った。N が偶数の場合は一般に同様のことが言える。

一応 N が奇数の場合も考えてみると、真ん中あたりで選択肢が 2 つある。下図の赤線で示した 2 つのラインは、大きい方を採用する感じ。

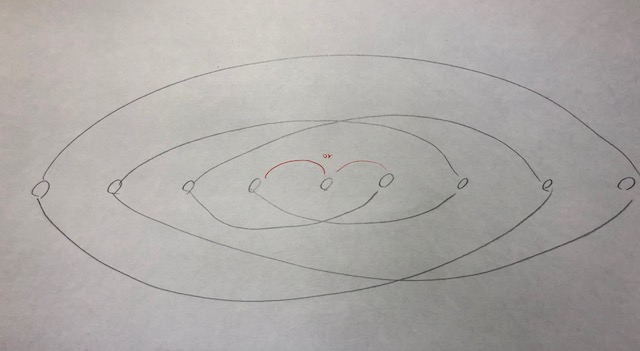
実装上は、上図の感じをなんとかコードにした感じ。

#include <iostream>
#include <vector>
#include <algorithm>
using namespace std;

int main() {
    int N; cin >> N;
    vector<long long> A (N);
    for (int i = 0; i < N; ++i) cin >> A[i];
    sort(A.begin(), A.end());

    long long res = A[N-1] - A[0];
    for (int i = 0, j = N-2; i + 1 < j; ++i, --j) res += A[j] - A[i];
    for (int i = 1, j = N-1; i + 1 < j; ++i, --j) res += A[j] - A[i];
    if (N & 1) res += max(A[N/2 + 1] - A[N/2], A[N/2] - A[N/2-1]);
    cout << res << endl;
}

editorial を読んで

editorial の解法の方がずっと筋がいいと思う。僕は

• b-a, c-b といった各区間が最大で何回加算されうるか

という視点で考えたが、editorial は

• 並びは「a > b < c > d < e > ... 」または「a < b > c < d > e < ...」としてよくて、a, b, c, d, e, f が何回ずつ足し引きされるかを考える

という視点だった。

例えば N = 9 の場合は数列は

• a1 > a2 < a3 > a4 < a5 > a6 < a7 > a8 < a9
• a1 < a2 > a3 < a4 > a5 < a6 > a7 < a8 > a9

の形だと決め打ちしてよくて、前者だと合計値は

• a1 - a2
• a3 - a2
• a3 - a4
• a5 - a4
• a5 - a6
• a7 - a6
• a7 - a8
• a9 - a8

を合計したものになるので

• a1 は 1 回
• a2 は -2 回
• a3 は 2 回
• a4 は -2 回
• a5 は 2 回
• a6 は -2 回
• a7 は 2 回
• a8 は -2 回
• a9 は 1 回

合計したものになることがわかる。よって、数列を大きい順に

• 2, 2, 2, 1, 1, -2, -2, -2, -2

回ずつ掛けて足せばいい。後者だと

• 2, 2, 2, 2, -1, -1, -2, -2, -2

になる。

一般に N が偶数のときは

• 2, 2, 2, 2, 1, -1, -2, -2, -2, -2 (2 と -2 が同数)

のようになって、N が奇数のときは

• 2, 2, 2, 1, 1, -2, -2, -2, -2 (-2 が 2 より 1 個多い)
• 2, 2, 2, 2, -1, -1, -2- -2, -2 (2 が -2 より 1 個多い)

という感じになる

#include <iostream>
#include <vector>
#include <algorithm>
using namespace std;

int main() {
    int N; cin >> N;
    vector<long long> A(N);
    for (int i = 0; i < N; ++i) cin >> A[i];
    sort(A.begin(), A.end(), greater<long long>());

    if (N % 2 == 0) {
        long long res = 0;
        for (int i = 0; i < N/2 - 1; ++i) res += A[i] * 2;
        res += A[N/2 - 1];
        res -= A[N/2];
        for (int i = N/2 + 1; i < N; ++i) res -= A[i] * 2;
        cout << res << endl;
    }
    else {
        long long res1 = 0;
        for (int i = 0; i < N/2 - 1; ++i) res1 += A[i] * 2;
        res1 += A[N/2 - 1] + A[N/2];
        for (int i = N/2 + 1; i < N; ++i) res1 -= A[i] * 2;
        
        long long res2 = 0;
        for (int i = 0; i < N/2; ++i) res2 += A[i] * 2;
        res2 -= A[N/2] + A[N/2 + 1];
        for (int i = N/2 + 2; i < N; ++i) res2 -= A[i] * 2;
        cout << max(res1, res2) << endl;
    }
}