sky さんの提唱した、代々伝わる名問題！！！

問題概要

$N$ 人の選手が箱根駅伝を走っている。テレビの放送では中継所で各チームの通過順位と共に前の中継所からの順位変動が表示される。

ある中継所を $1, 2, \dots, N$ 番目に通過したそれぞれの選手について、前回の中継所と比べて

順位は不変 (文字 '-' で表す)
順位が上昇した (文字 'U' で表す)
順位が下降した (文字 'D' で表す)

のいずれかの状態が明かされる。各選手の前回の中継所を通過した順位として考えられる場合の数を 1000000007 で割ったあまりを求めよ。

制約

$1 \le N \le 200$

考えたこと

$1, 2, \dots, N$ の順列のうち条件を満たすものの個数を数え上げるタイプの問題。この手の問題に対しては

bit DP
挿入 DP
箱根駅伝 DP (むしろこの問題がその名の由来)
swap するような DP (CPSCO day3-F など)

などの方法が考えられる。このうち bit DP は $N \le 20$ くらいまでしか解けない。挿入 DP はボールの並び替えの個数を数えるのによく使える。ここでは

順列とマッチングとを対応させる

という技術で解いてみることにする。順列とマッチングとを対応させる考え方そのものは、数え上げ問題に限らず典型的。

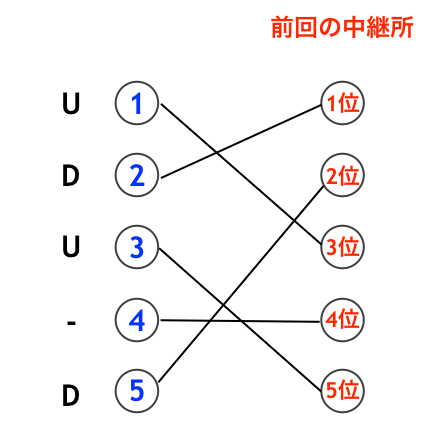
f:id:drken1215:20191005022741p:plain

箱根駅伝 DP

$(1, 2, \dots, N)$ と $(1, 2, \dots, N)$ とのマッチングのうち、条件を満たすものを数え上げたりする DP では、

dp[i][j] := $(1, 2, \dots, i)$ と $(1, 2, \dots, i)$ 同士のみを考えたときに、マッチングしている箇所が j 箇所であるような場合の数

とすることで解決できる場合がある。こういうのを箱根駅伝 DP とよんだりしてる。

f:id:drken1215:20191005171045p:plain

さて、 $i$ から $i + 1$ への遷移を考える。ここでは今回の問題に限らず、一般的な箱根駅伝の雰囲気を伝えるための、一般論で考えてみる。以下の 5 パターンがある

左側の頂点 $i+1$ からも、右側の頂点 $i+1$ からも上に行く場合
左側の頂点 $i+1$ からは上に行き、右側の頂点 $i+1$ からは下に行く場合
左側の頂点 $i+1$ からは下に行き、右側の頂点 $i+1$ からは上に行く場合
左側の頂点 $i+1$ と、右側の頂点 $i+1$ がマッチングする場合
左側の頂点 $i+1$ からも、右側の頂点 $i+1$ からも下に行く場合

左側の頂点 $i+1$ からも、右側の頂点 $i+1$ からも上に行く場合

下図のような感じ。こういうときはマッチングが 2 本増えて、 $j$ 本から $j+2$ 本になる。つまり、

dp[i+1][j+2] += dp[i][j] * (i - j) * (i - j);

という感じの遷移になる。なぜなら、

左側の頂点 $i + 1$ にとって、右側の頂点 $1, 2, \dots, i$ のうち、まだマッチングしていない頂点は $i - j$ 個
右側の頂点 $i + 1$ にとって、左側の頂点 $1, 2, \dots, i$ のうち、まだマッチングしていない頂点は $j - i$ 個

あるからだ。

f:id:drken1215:20191005165259p:plain

最大のポイントは

$(1, 2, \dots, i)$ と $(1, 2, \dots, i)$ のうちどこがマッチングしているかを知らなくても、まだマッチングしていないノードが何箇所あるかだけわかれば遷移を作れる

というところだ。

左側の頂点 $i+1$ からは上に行き、右側の頂点 $i+1$ からは下に行く場合

下図のような感じ。このとき、左側の $(1, 2, \dots, i+1)$ と右側の $(1, 2, \dots, i+1)$ とでマッチングされている辺が $j + 1$ 本になるので

dp[i+1][j+1] += dp[i][j] * (i - j);

という感じの遷移になる。 $i - j$ をかけるところはさっきと一緒。

f:id:drken1215:20191005165616p:plain

左側の頂点 $i+1$ からは下に行き、右側の頂点 $i+1$ からは上に行く場合

さっきの左右反転。

左側の頂点 $i+1$ と、右側の頂点 $i+1$ がマッチングする場合

下図のような感じ。左側の頂点 $(1, 2, \dots, i+1)$ と右側の頂点 $(1, 2, \dots, i+1)$ とでマッチングされている辺が $j + 1$ 本になるので

dp[i+1][j+1] += dp[i][j];

という感じの遷移になる。今回は $i - j$ は特にかけない。

f:id:drken1215:20191005170025p:plain

左側の頂点 $i+1$ からも、右側の頂点 $i+1$ からも下に行く場合

下図のような感じ。マッチング辺は増えず、 $j$ 本のままで

dp[i+1][j] += dp[i][j];

という感じの遷移になる。

f:id:drken1215:20191005170741p:plain

計算量

以上のような DP で計算量は $O(N^{2})$ となる。

今回の問題の場合

今回の問題でも、以上の箱根駅伝 DP を少しいじるだけで解くことができる。ただし、各左側頂点について

上で伸びるべきか
下に伸びるべきか

があらかじめ決まっているので、それに従えば OK。具体的には、

'-' のとき

以下の場合のみ

左側の頂点 $i+1$ と、右側の頂点 $i+1$ がマッチングする場合

'U' のとき

左側の頂点 $i+1$ からは右側に向かって下に伸びることになるので、以下の場合を考えれば良い。

左側の頂点 $i+1$ からは下に行き、右側の頂点 $i+1$ からは上に行く場合
左側の頂点 $i+1$ からも、右側の頂点 $i+1$ からも下に行く場合

'D' のとき

左側の頂点 $i+1$ からは右側に向かって上に伸びることになるので、以下の場合を考えれば良い。

左側の頂点 $i+1$ からも、右側の頂点 $i+1$ からも上に行く場合
左側の頂点 $i+1$ からは上に行き、右側の頂点 $i+1$ からは下に行く場合

計算量

計算量はやはり $O(N^{2})$ である。

#include <iostream>
#include <vector>
using namespace std;


// modint: mod 計算を int を扱うように扱える構造体
template<int MOD> struct Fp {
    long long val;
    constexpr Fp(long long v = 0) noexcept : val(v % MOD) {
        if (val < 0) v += MOD;
    }
    constexpr int getmod() { return MOD; }
    constexpr Fp operator - () const noexcept {
        return val ? MOD - val : 0;
    }
    constexpr Fp operator + (const Fp& r) const noexcept { return Fp(*this) += r; }
    constexpr Fp operator - (const Fp& r) const noexcept { return Fp(*this) -= r; }
    constexpr Fp operator * (const Fp& r) const noexcept { return Fp(*this) *= r; }
    constexpr Fp operator / (const Fp& r) const noexcept { return Fp(*this) /= r; }
    constexpr Fp& operator += (const Fp& r) noexcept {
        val += r.val;
        if (val >= MOD) val -= MOD;
        return *this;
    }
    constexpr Fp& operator -= (const Fp& r) noexcept {
        val -= r.val;
        if (val < 0) val += MOD;
        return *this;
    }
    constexpr Fp& operator *= (const Fp& r) noexcept {
        val = val * r.val % MOD;
        return *this;
    }
    constexpr Fp& operator /= (const Fp& r) noexcept {
        long long a = r.val, b = MOD, u = 1, v = 0;
        while (b) {
            long long t = a / b;
            a -= t * b; swap(a, b);
            u -= t * v; swap(u, v);
        }
        val = val * u % MOD;
        if (val < 0) val += MOD;
        return *this;
    }
    constexpr bool operator == (const Fp& r) const noexcept {
        return this->val == r.val;
    }
    constexpr bool operator != (const Fp& r) const noexcept {
        return this->val != r.val;
    }
    friend constexpr ostream& operator << (ostream &os, const Fp<MOD>& x) noexcept {
        return os << x.val;
    }
    friend constexpr istream& operator >> (istream &is, Fp<MOD>& x) noexcept {
        return is >> x.val;
    }
    friend constexpr Fp<MOD> modpow(const Fp<MOD> &a, long long n) noexcept {
        if (n == 0) return 1;
        auto t = modpow(a, n / 2);
        t = t * t;
        if (n & 1) t = t * a;
        return t;
    }
};

using mint = Fp<1000000007>;
mint dp[210][210];

int main() {
    int N; cin >> N;
    vector<char> v(N);
    for (int i = 0; i < N; ++i) cin >> v[i];

    dp[0][0] = 1;
    for (int i = 0; i < N; ++i) {
        for (int j = 0; j <= N; ++j) {
            if (v[i] == '-') {
                dp[i+1][j+1] += dp[i][j];
            }
            else if (v[i] == 'U') {
                dp[i+1][j+1] += dp[i][j] * (i - j);
                dp[i+1][j] += dp[i][j];
            }
            else {
                dp[i+1][j+2] += dp[i][j] * (i - j) * (i - j);
                dp[i+1][j+1] += dp[i][j] * (i - j);
            }
        }
    }
    cout << dp[N][N] << endl;
}

けんちょんの競プロ精進記録

競プロの精進記録や小ネタを書いていきます

AOJ 2439 箱根駅伝 (JAG 夏合宿 2012 day3a-F) (600 点)

問題概要

制約

考えたこと