2019-12-17

動的計画法で求めた解を全列挙する方法

DP 復元最適解の数え上げ部分和テーマ解説記事勤怠を題材とした問題ナップサックDP

きっかけは、タピオカ流競プロ優勝ガール、マリーさんのツイートでした。

100個ぐらいある整数から自由に選んでK円になる組み合わせを探せ！複数通りある場合は列挙！みたいな仕事がだるすぎてdpで列挙してくれるやつ作った
競プロは事務員を救う
— マリー (@CBOX360) 2019年12月17日

【悲報】1通りしか探せない
— マリー (@CBOX360) 2019年12月17日

マリーお姉ちゃんはタピオカ屋の事務員です。
入金日に全部でまとめてK円入金され、N件の請求済みデータの中からいくつか選んで入金済みにステータス変更をしたいと思っています。
請求済みデータの金額はa1,a2…aN円です。
組み合わせが複数ある場合は、店長に問い合わせをするので列挙してください。
— マリー (@CBOX360) 2019年12月17日

つまり、

部分和問題で「総和が $K$ 」とできるかどうかは求められる
ちょっと工夫すれば「総和が $K$ となる方法が何通りか」までは求められる

でも

総和が $K$ になる方法を全列挙する方法がわからない

というものでした。この全列挙する方法を考えます。

注意

総和が $K$ になる場合の数があまりにも多いと爆発します。ここでは入力データの性質から、せいぜい 10 通りくらいになることを想定します。

1. DP における経路復元

DP で求めた解を復元する方法論については、以下の記事にまとめたことがあります。

qiita.com

この記事の方法に従えば、「答えを 1 つ復元する」ことができるようになります。そして、「答えをすべて列挙する」というのも、実はほんのちょっと頑張るだけで実施することができるようになります。

その前に一度、部分和問題に対する DP がどんなものだったかを振り返っておきます。

2. 部分和問題に対する DP とは

ここでは、まずは以下の問題を考えてみましょう。

$N$ 個の正の整数 $a_{1}, a_{2}, \dots, a_{N}$ と、正の整数 $K$ が与えられます。

$N$ 個の整数からいくつか選んだ総和が $K$ となる方法が何通りあるかを求めてください。

この問題は、よくある DP で解くことができます。

dp[ i ][ j ] := $N$ 個の整数のうち、最初の $i$ 個のみを用いて、総和を $j$ にする方法が何通りあるか

として、

dp[ i + 1 ][ j ] += dp[ i ][ j ]
dp[ i + 1 ][ j + a[ i ] ] += dp[ i ][ j ]

という遷移で DP すればよいです (ここでは「配る DP」で書いています)。

さて、この DP って、たとえば $N = 5$ 、 $K = 10$ 、 $a = (1, 2, 3, 4, 5)$ のとき、下図のようなグラフで「左上」から「右下」まで行くパスは何通りあるますかという問題なんですね。図中の各ノードの数値は、「左上」からそのノードに行くのに何通りあるかを書いています。

3. DP テーブルを遡るようにして復元

つまり、左上から右下まで行くのに 3 通りということになります。次にこの 3 通りを列挙する方法を考えてみましょう。これは、上のようにして求めた DP テーブルを逆流すると良いです。

まず、右下の「3」に伸びている矢印が 2 本あります。これらはそれぞれ

(4, 5) マスまで至る方法は 2 通りあって、そこから a = (1, 2, 3, 4, 5) のうちの最後の 5 を選んで (4, 10) に至る
(4, 10) マスまで至る方法は 1 通りあって、そこから何も選ばずに (4, 10) に至る

ということを表しています。さらに遡ります。

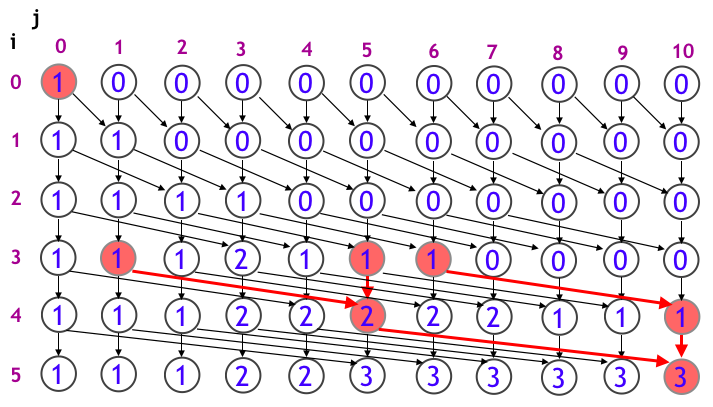
注意点として、矢印を遡ったときに「0」になるところは枝刈りしてよいです。なぜなら「0 通り」のノードにはスタートから辿り着くことができないからです。よって、上図でいえば (3, 10) のマスに遡る必要はありません。この枝刈りが本質で、これをやらないと、わざわざ DP テーブルを作った意味がないです！！！！！！

この調子で繰り返すと下のようになります。

これらを解釈すると

「1 を選ばない」「2 を選ぶ」「3 を選ぶ」「4 を選ばない」「5 を選ぶ」(2 + 3 + 5 = 10)
「1 を選ぶ」「2 を選ばない」「3 を選ばない」「4 を選ぶ」「5 を選ぶ」 (1 + 4 + 5 = 10)
「1 を選ぶ」「2 を選ぶ」「3 を選ぶ」「4 を選ぶ」「5 を選ばない」 (1 + 2 + 3 + 4 + 10)

の 3 通りの経路が復元できていることがわかります。この復元の様子を実装すると、下のように書けます。

#include <iostream>
#include <vector>
#include <deque>
#include <algorithm>
using namespace std;

const int MAX = 1000;

void rec(const vector<vector<long long>> &dp, const vector<int> &a, int i, int j, deque<int> &keiro, vector<deque<int>> &ans) {
    if (i == 0) {
        if (j == 0) {
            ans.push_back(keiro);
        }
        return;
    }

    // 上へ遡る (dp[i-1][j] == 0) だったら無視)
    if (dp[i-1][j]) {
        rec(dp, a, i-1, j, keiro, ans);
    }
    // 左上へ遡る (dp[i-1][j-a[i-1]] == 0 だったら無視)
    if (j-a[i-1] >= 0 && dp[i-1][j-a[i-1]]) {
        keiro.push_front(a[i-1]);
        rec(dp, a, i-1, j-a[i-1], keiro, ans);
        keiro.pop_front();
    }
}


int main() {
    int N, X;
    cin >> N >> X;
    vector<int> a(N);
    for (int i = 0; i < N; ++i) cin >> a[i];

    // DP
    vector<vector<long long>> dp(N+1, vector<long long>(MAX, 0));
    dp[0][0] = 1;
    for (int i = 0; i < N; ++i) {
        for (int j = 0; j < MAX; ++j) {
            dp[i+1][j] += dp[i][j];
            if (j + a[i] < MAX) dp[i+1][j+a[i]] += dp[i][j];
        }
    }

    // 復元
    deque<int> keiro;
    vector<deque<int>> ans;
    rec(dp, a, N, X, keiro, ans);

    // 出力
    cout << "the num of combinations is: " << ans.size() << endl;
    for (int i = 0; i < ans.size(); ++i) {
        cout << i+1 << " case:";
        for (auto el : ans[i]) cout << " " << el;
        cout << endl;
    }
}

4. 最終形

マリーさんの問題に対するコードは、最終的には以下の感じになった。

タピオカ事務員さん問題の改良版です

・1 円単位に対応
・K 円を超えない範囲で、なるべく K に近いものを上位 5 件出力https://t.co/NQwMmolx19
— けんちょん (@drken1215) 2019年12月17日

5. 発展

今回の方法は割と汎用的で、あらゆる DP に適用できる復元方法ではあります。あと、関連する話として、見た目が復元を要求する問題ではなかったとしても、

最適解に使われうる辺を列挙して
その辺のみに考察対象を絞って色々やる

みたいな問題も割とよく見る気がします。

けんちょんの競プロ精進記録

競プロの精進記録や小ネタを書いていきます