ビット全探索もついに茶色 diff ですね!
予備知識
ビット全探索の知識があると解きやすいです!
問題概要
英小文字のみからなる 個の文字列
が与えられます。
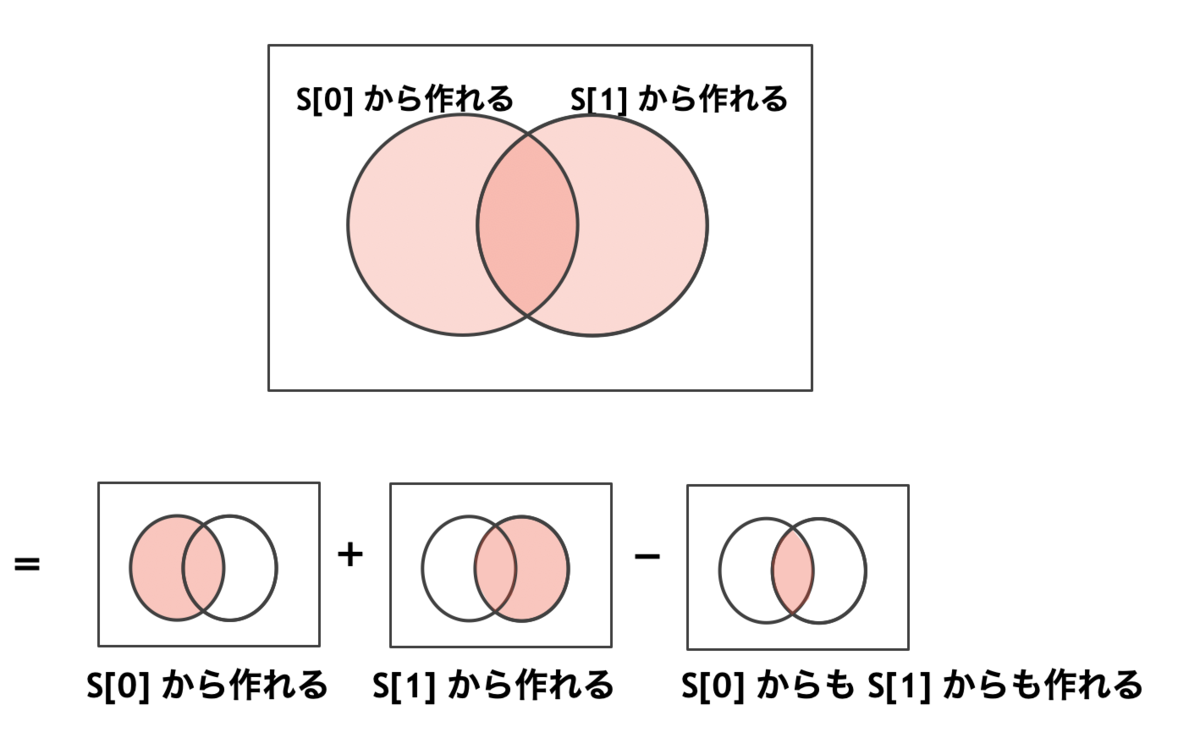
これらの文字列の中から、いくつかの文字列を選びます。
こうして選んだ文字列のうち、ちょうど 個に含まれているような文字の種類を数えます。その種類数として考えられる最大値を求めてください。
制約
一目で bit 全探索!!
問題の意味がパッと分かりづらいですね。でも種類数がナンタラのところがパッと分からなかったとしても、「この問題が bit 全探索で解けそうだ」ということは一目でわかります。それは
個のものから、いくつか選んだ結果を最適化する問題だということ
- 制約が
というように、思わせぶりであること
の 2 つが理由です!!!
まず 1 個目についてですが、競プロではまさに 個のものからいくつか選んだ結果を最適化する問題が数多いです。ナップサック問題もそうですね。
そういう問題は、制約さえ小さければ、必ず bit 全探索で解けるのです。そう思っているところに「」という制約があるのですから、bit 全探索確定です!!
bit 全探索
個のものからいくつか選んで得られる集合は
通りあります。そのような集合たちをビットで表します。 そして bit 全探索は、次のように書けます。
for (int bit = 0; bit < (1 << N); ++bit) { // ビットで表すと bit になるような集合を調べる }
たとえば N = 8 で bit = 0b01100111 のとき、8 個のもの (0〜7) のうち 0, 1, 2, 5, 6 番目のものを選ぶような場合を表します。ビット表現では、右端の桁から順に i 桁目が 1 のときは「i 番目のものを選ぶ」ことを表し、i 桁目が 0 のときは「i 番目のものを選ばない」ことを表します。
なお、調べる集合の個数は 通りあります。多くの場合、各集合を評価するのに要する計算量は
ですので、全体の計算量は
になることが多いです。各集合の評価により多くの時間がかかりときは、全体の計算量もより大きくなります。
集合 bit を調べる
最後に、今回の問題において、 個のもののうち、ビット表現で bit と表される集合が条件を満たすかどうかを調べる部分を詰めます。
'a' から 'z' までの 26 種類の各文字について、それが何回登場するかを数えてあげます。そして、ちょうど 回登場するものが何文字あるかを数えましょう。
たとえば次のように実装できます。bit に対して、そのスコア ( 回登場する文字の個数) を評価する関数を実装します。
int evaluate(int bit, int N, int K, const vector<string>& S) { int res = 0; // num[c] := 文字 c (0〜26 で表す) の登場回数 vector<int> num(26, 0); for (int i = 0; i < N; ++i) { // bit に S[i] が含まれないならスキップ if (!(bit & (1 << i))) continue; // S[i] に含まれる文字をカウントしていく for (char c : S[i]) num[c - 'a']++; } // num[c] = K となる文字 c を数える for (int c = 0; c < 26; ++c) if (num[c] == K) ++res; return res; }
コード
計算量は、英小文字の種類数を としたとき、
bitの個数:通り
- 関数
evaluate(bit):
ですので、全体として となります。今回は
,
ですので十分間に合います。
#include <bits/stdc++.h> using namespace std; int evaluate(int bit, int N, int K, const vector<string>& S) { int res = 0; // num[c] := 文字 c (0〜26 で表す) の登場回数 vector<int> num(26, 0); for (int i = 0; i < N; ++i) { // bit に S[i] が含まれないならスキップ if (!(bit & (1 << i))) continue; // S[i] に含まれる文字をカウントしていく for (char c : S[i]) num[c - 'a']++; } // num[c] = K となる文字 c を数える for (int c = 0; c < 26; ++c) if (num[c] == K) ++res; return res; } int main() { int N, K; cin >> N >> K; vector<string> S(N); for (int i = 0; i < N; ++i) cin >> S[i]; // ビット全探索 int res = 0; for (int bit = 0; bit < (1 << N); ++bit) { res = max(res, evaluate(bit, N, K, S)); } cout << res << endl; }