けんちょんの競プロ精進記録

競プロの精進記録や小ネタを書いていきます

AtCoder ABC 124 D - Handstand (緑色, 400 点)

AtCoder AtCoder400点 ABC-D 区間 操作 XOR 0と1の問題 数列 しゃくとり法 累積和 二分探索 最適化テク:最適解の形を考える 最適化テク：変形しても悪化しない 最適化テク:探索候補を絞る 最適化テク:操作の流れを単純化する 操作後の結果の最適化問題 操作:flip 最大スコア 緑色diff 区間の長さの最大値または最小値を求める テク:区間の交差関係や包含関係を除去できる テク:2点や2区間の配置関係を考える disjointな区間の集合を管理する問題 操作をK回まで行える ランレングス圧縮 テク:区間ごとに分割する 操作:区間 典型要素を詰め合わせた教育的問題 最適化問題

これ...以前 Twitter につぶやいた問題とよく似てた！！！

解法の考え方もだいたい一緒で、最後の詰めがちょっと違う感じ。

問題へのリンク

問題概要

N 要素の 0 と 1 から成る数列が与えられる。

「数列の区間を選んで 0 と 1 をフリップする」という操作を最大 K 回行なって作ることのできる数列のうち、 1 が連続している部分の連続長さが最大となるようにしたい。その最大長さを求めよ。

制約

  • 1 \le N, K \le 10^{5}

考えたこと

まず区間に対するフリップ操作に関する問題で考えると良さそうなこととして

  • 区間が互いに交差しないものとして扱えないか (他に区間の終端でソートして考えるなども)
  • いもす法変換によって、区間に対する操作を 2 点に対する操作として扱えないか

といったことが挙げられると思う。今回は 1 番目の方針がドンピシャになる。

区間操作が互いに交差しないものとしてよい

複雑に絡み合う区間への操作を考えるのは大変なので、「交差する区間への操作」と、「交差しない区間への操作」が同じ結果をもたらすならば後者を採用したい。

今回ドンピシャで下図のように、区間 a への操作と、区間 b への操作が交差していたとしても、それは交差していない 2 つの区間への操作と同じ結果をもたらすので、後者で置き換えることができる。

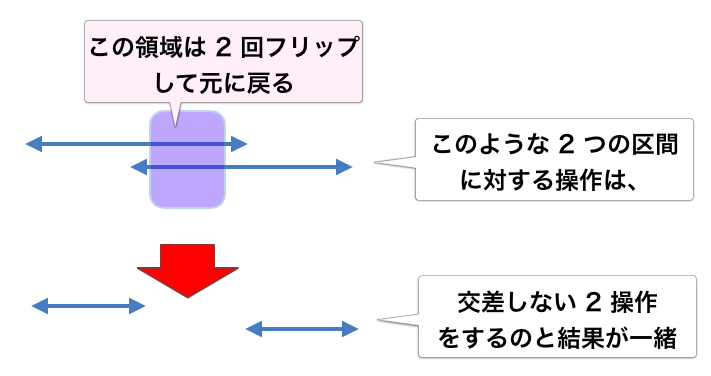
よって、「どの 2 つの区間も交差しないケース」に限定したとしても、作れることのできる数列の種類は変わらないということがわかったので、どの 2 つの区間も交差しないケースだけを考えることにする。これで一気に考察が楽になった。

例えば K = 2 だったら、下図の青い区域のうち 2 つを選んで区域全体を 1 にすることで、最長の 1 の長さはどうなるかを問う問題ということになる。

例えばこの図の場合は、以下の 2 つの区域を選ぶと、1 の連続数が最大になる。

雰囲気としては、

  • 連続した K 個の青領域についてフリップして
  • できあがる 1 の連続数の最大値を求める

という風になる。これをシンプルにした問題としては

N 個の数列 a_1, a_2, \dots, a_N があって、その連続する K 個の整数の総和として考えられる最大値を求めよ

というものがあって、これは累積和やしゃくとり法で O(N) で高速に解くことができる (累積和による解説はこれに書いた、しゃくとり法による解説はこの paiza のページなどを参照)。

今回の問題も、若干面倒にはなっているけど、同じように解くことができる。ここでは累積和で解いてみる。まず、「0 の個数」と「1 の個数」を交互に書き出してみる。紛らわしさを防ぐために、両端が「1」じゃないならば、両端に「0 個の 1」があるものとみなして 0 を書いておく。 例えば図の例だと、

0, 1, 1, 2, 1, 3, 2, 2, 1, 1, 1

といった具合になる。これは

  • 0, 2, 4, ... 番目の値は「連続する 1 の個数」
  • 1, 3, 5, ... 番目の値は「連続する 0 の個数」

を表している。そこで、例えば K = 2 であれば

  • 0, 1, 1, 2, 1 の和 (「連続する 0 の区間」を間に 2 個挟んでいる)
  • 1, 2, 1, 3, 2 の和 (「連続する 0 の区間」を間に 2 個挟んでいる)
  • 1, 3, 2, 2, 1 の和 (「連続する 0 の区間」を間に 2 個挟んでいる)
  • 2, 2, 1, 1, 1 の和 (「連続する 0 の区間」を間に 2 個挟んでいる)

のうちの最大値を求めればよいことがわかる。まとめると、「0, 2, 4, ... 番目から始まる連続する 2K+ 1 個 (以下) の整数の和の最大値」を求めればよい。

コード

#include <iostream>
#include <string>
#include <vector>
using namespace std;

int main() {
    int N, K; cin >> N >> K;
    string S; cin >> S;

    // 「1 の個数」「0 の個数」を交互に記録していく
    vector<int> nums;    
    if (S[0] == '0') nums.push_back(0); // 先頭が 0 だったら
    for (int i = 0; i < S.size();) {
        int j = i;
        while (j < S.size() && S[j] == S[i]) ++j; // S[i] の数値がどこまで続くか
        nums.push_back(j - i);
        i = j;
    }
    if (S.back() == '0') nums.push_back(0); // 最後尾が 0 だったら

    // 累積和
    vector<int> sums((int)nums.size() + 1, 0);
    for (int i = 0; i < nums.size(); ++i) sums[i+1] = sums[i] + nums[i];

    // 偶数番目の添字から始まる、長さ 2K+1 (以下) の区間の総和のうち、最大値を求める
    int res = 0;
    for (int left = 0; left < sums.size(); left += 2) {
        int right = left + K*2+1;
        if (right >= sums.size()) right = (int)sums.size() - 1;
        res = max(res, sums[right] - sums[left]);
    }
    cout << res << endl;
}