けんちょんの競プロ精進記録

競プロの精進記録や小ネタを書いていきます

AtCoder ABC 125 D - Flipping Signs (緑色, 400 点)

AtCoder AtCoder400点 ABC-D パリティ 不変量 数列 条件の言い換え 操作 操作:隣接swap 補集合を考える 操作後の結果の最適化問題 最大スコア 緑色diff 最適化問題

操作をいい感じに言い換える感じ

問題へのリンク

問題概要

N 個の要素 A_1, A_2, \dots, A_N が与えられる。これに対し、以下の操作を好きなだけ行える。

  • 隣り合う 2 要素をともに -1 倍する

操作後の数列の値の和として考えられる最大値を求めよ。

制約

  • 2 \le N \le 10^{5}
  • -10^{9} \le A_i \le 10^{9}

考えたこと

こういう「操作」に関する問題では、「操作がどんなものなのかをわかりやすく言い換える」ということがポイントになることが多い。とりあえず下図のように、「+」「-」が並んでいる箇所に対して操作すると「-」「+」になるが、これを

  • 「-」の左が「+」のとき、「-」を左に動かすことができる

という風に解釈することができる。同様にして、「-」「+」の並びも「+」「-」にすることができて、これは

  • 「-」の右が「+」のとき、「-」を右に動かすことができる

と解釈することができる。

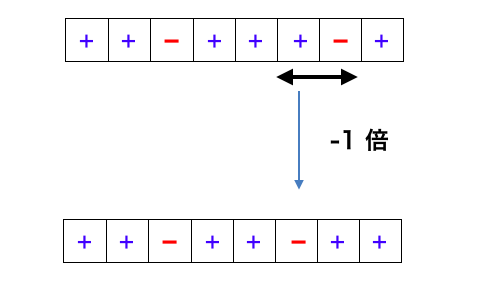
そしてこの解釈を実践すると

  • 「-」を一箇所に集めることができる

ということが言える。さらに一箇所に集めた上で、ペアにして消すことができる。

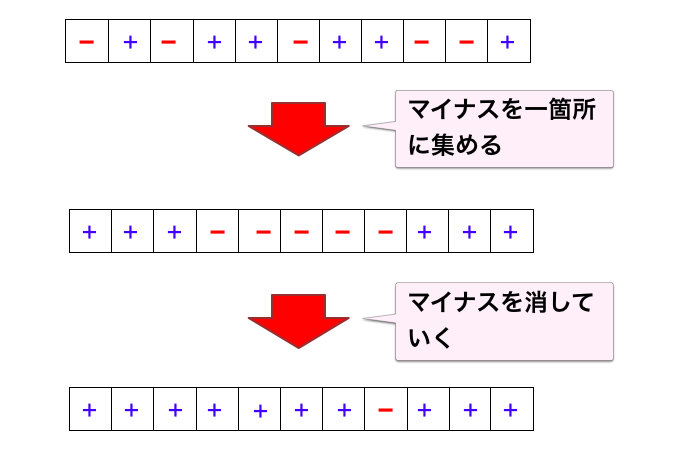
このとき

  • マイナスが偶数個だったらマイナス全部消せる
  • マイナスが奇数個だったらマイナスが 1 個だけ残る (ちゃんとした証明は記事の最後に後述)

ということがわかる。前者の場合の答えはもう明らかで、 A_1, A_2, \dots, A_N をすべてプラスにして足せば OK。後者の場合に最後に気になるのは

  • 1 個だけ残ってしまうマイナスをどこにつけるか？

であるが、マイナスは好きなように左右に動かせることがすでにわかっているので、 A_1, A_2, \dots, A_N のうち一番絶対値が小さいところにマイナスをつければ OK。

#include <iostream>
#include <vector>
using namespace std;

template<class T> inline bool chmax(T& a, T b) { if (a < b) { a = b; return 1; } return 0; }
template<class T> inline bool chmin(T& a, T b) { if (a > b) { a = b; return 1; } return 0; }

int main() {
    int N; cin >> N;
    vector<long long> a(N);
    for (int i = 0; i < N; ++i) cin >> a[i];
    int num_minus = 0;
    long long mi = 1LL<<60;
    long long sum = 0;
    for (int i = 0; i < N; ++i) {
        if (a[i] < 0) ++num_minus;
        chmin(mi, abs(a[i]));
        sum += abs(a[i]);
    }
    if (num_minus % 2 == 0) cout << sum << endl;
    else cout << sum - mi*2 << endl;
}

マイナスが初期に奇数個のときに必ず 1 個残ること

マイナスが最初奇数個だったときは、どんなに頑張っても必ず 1 個残ってしまうことを一応証明してみる。そんなに難しくなくて、いかなる方法で操作を行っても、

  • マイナスの個数のパリティ (偶数か奇数か) は不変である (マイナスの個数は 2 個減るか、変わらないか、2 個増えるかのいずれかなので)

ということが言える。こういうのを不変量という。この問題では不変量が割と明らかではあるけど、高難易度では非自明な不変量を見出すことがポイントになる問題も多い気がする。

で、マイナスの個数は最初奇数個だったらずっと奇数個なので、0 個にすることはできない。