AtCoder ABC 051 C - Back and Forth (緑色, 300 点)

ちょっとした構築系問題という感じかな...

問題へのリンク

問題概要

二次元平面上の二点 が与えられる。 はすべて整数である。

今、 から出発して「上下左右に 1 秒に 1 だけ動く」という動作を繰り返しながら に行き、またそこから出発して に戻り、さらにまた に行って、 に戻りたい。

ただし、往復する過程で「同じ座標」を二度通ってはいけない。最短時間で往復を実現する経路を 1 つ求めよ。

制約

• 
• 

考えたこと

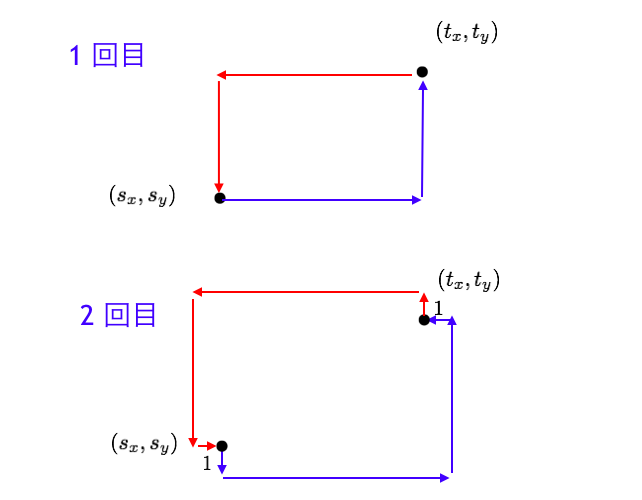
下図みたいな動きをすれば OK。1 回目と 2 回目ともに

• 青線で行って
• 赤線で帰る (赤線ではほんの少しだけ寄り道をする)

ここで、 と との位置関係が気になるが、問題文によると常に は の右上にあるので大丈夫。

#include <iostream>
#include <string>
using namespace std;

int main() {
    int sx, sy, tx, ty;
    cin >> sx >> sy >> tx >> ty;
    int dx = tx - sx, dy = ty - sy;
    
    string res = "";

    // 1 回目
    for (int i = 0; i < dx; ++i) res += "R";
    for (int i = 0; i < dy; ++i) res += "U";
    for (int i = 0; i < dx; ++i) res += "L";
    for (int i = 0; i < dy; ++i) res += "D";

    // 2 回目
    res += "D";
    for (int i = 0; i <= dx; ++i) res += "R";
    for (int i = 0; i <= dy; ++i) res += "U";
    res += "L";
    res += "U";
    for (int i = 0; i <= dx; ++i) res += "L";
    for (int i = 0; i <= dy; ++i) res += "D";
    res += "R";
    cout << res << endl;
}