条件反射でいもす法をしたけれど、もっと楽にできた

そして手前味噌ながら類題

問題概要

$M$ 個の区間 $\lbrack l_i, r_i \rbrack$ があたえられる。 $1 \le l_i \le r_i \le N$ を満たしている。

この区間が $M$ 重に交わっている部分の長さを求めよ。

制約

$1 \le N, M \le 10^{5}$

解法 1：区間の交差

区間 $\lbrack a, b \rbrack$ と $\lbrack c, d \rbrack$ の交差は実は簡単にかけて

$\lbrack \max(a, c), \min(b, d) \rbrack$ 　(左端が $\max(a, c)$ で右端が $\min(b, d)$ )

になる。面倒な場合分けが要らない！！！
ただし $\max(a, c) \gt \min(b, d)$ の場合は「交差しない」ということになる。

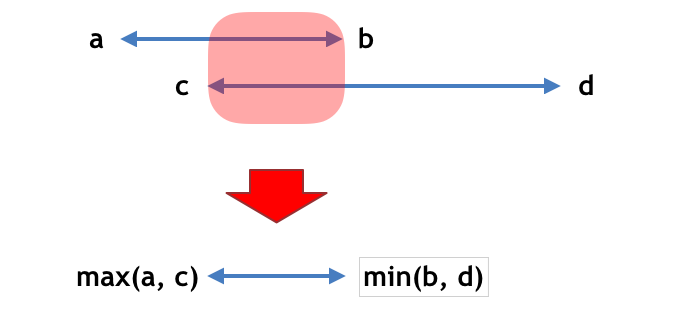
このことを利用して、 $N$ 個の区間の交差は

$\lbrack \max(l_1, l_2, \dots, l_N), \min(r_1, r_2, \dots, r_N) \rbrack$

と表せる。これを $\lbrack L, R \rbrack$ と表したとき、

$L \le R$ なら、 $R - L + 1$ が答え
$L \gt R$ なら、 $0$ が答え

となる。

#include <iostream>
#include <vector>
using namespace std;

int main() {
    int N, M; cin >> N >> M;
    int left = 1, right = N;
    for (int i = 0; i < M; ++i) {
        int a, b; cin >> a >> b;
        left = max(left, a);
        right = min(right, b);
    }
    cout << max(right - left + 1, 0) << endl;
}

解法 2：いもす法

この問題の解説とほぼ同じことをすれば OK。

atcoder.jp

そして最後に、「出来上がった配列のうち、値が $M$ になっている部分を数える」とすればよい。

なお、下のコードで、 $l, r$ については 0-indexed で考えています。一方で、問題文で与えられているのは左閉区間・右閉区間ですが、いもす法を適用するために左閉区間・右開区間にしています。よって、

--l
--r
++r

をすることになって、 $r$ については結果的に入力のままとしています。

#include <iostream>
#include <vector>
using namespace std;

int main() {
    int N, M; cin >> N >> M;
    vector<int> G(N+1, 0);
    for (int i = 0; i < M; ++i) {
        int l, r; cin >> l >> r; --l;
        G[l]++;
        G[r]--;
    }
    for (int i = 0; i < N; ++i) G[i+1] += G[i];
    int res = 0;
    for (int i = 0; i < N; ++i) if (G[i] == M) ++res;
    cout << res << endl;
}

けんちょんの競プロ精進記録

競プロの精進記録や小ネタを書いていきます

AtCoder ABC 127 C - Prison (灰色, 300 点)

問題概要

制約

解法 1：区間の交差

解法 2：いもす法