AtCoder ABC 187 E - Through Path (水色, 500 点)

これの応用問題って感じだった！！

drken1215.hatenablog.com

• 問題へのリンク

問題概要

頂点数 の木が与えられる。 番目の辺は頂点 と頂点 とを結んでいる。はじめ、各頂点には、値 0 が書き込まれている。以下の 個のクエリを処理したあとの、各頂点に書き込まれた値を求めよ。

• クエリタイプ 1：辺番号 と、値 が与えられる。頂点 から出発して頂点 を通過することなくたどり着けるすべての頂点の値を だけ増やす
• クエリタイプ 2：辺番号 と、値 が与えられる。頂点 から出発して頂点 を通過することなくたどり着けるすべての頂点の値を だけ増やす

制約

• 

考えたこと

単純化した次の問題を考えてみよう。

• 与えられた木は根付き木であるとする
• 各クエリでは、頂点 を根とする部分木に含まれるすべての頂点の値を だけ増やす

この問題は実は過去問にそっくりそのままある！

drken1215.hatenablog.com

今回は、ちょっと応用問題と言える。というのも、まず与えられる木に根は指定されていない。よってまずは適当な頂点 (たとえば頂点 0) を根とした根付き木にしてしまおう。そして、クエリタイプ 1, 2 はいずれも、以下の 2 つの場合のいずれかの処理を行うことになる。

---

二頂点 があって、 が の親であるとする。

• パターン 1： を根とする根付き木全体に を足す
• パターン 2： を根とする根付き木以外の頂点に を足す

---

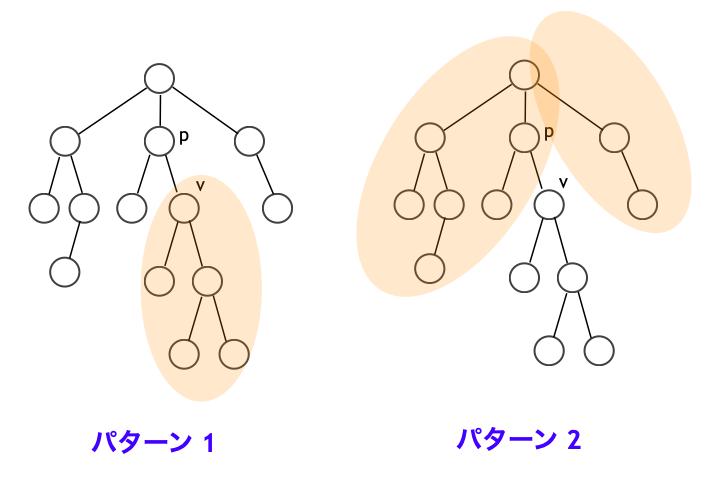
もともとのクエリタイプ 1, 2 が、このパターン 1, 2 にそのまま対応するとは限らない。いずれにしても、上に述べた 2 パターンのいずれかになる。

パターン 2 をパターン 1 へ帰着

さて、上のパターン 1 だけならば、まさに過去問の通りに解ける。パターン 2 があるのが厄介だ。しかしよく考えてみると、下図のように、パターン 2 はパターン 1 に帰着できるのだ！！！

つまり、パターン 2 は

• すべての頂点に を足す (別途保持しておいて最後にまとめて足す)
• 頂点 を根とする根付き木全体に を足す (パターン 1 と同じ処理)

というふうにすることで、結局すべてパターン 1 に帰着できる。

パターン 1

パターン 1 は、まさに次の問題そのものなので、以下の記事参照！

drken1215.hatenablog.com

コード

計算量は になる。

#include <bits/stdc++.h>
using namespace std;
using Graph = vector<vector<int>>;

int main() {
    int N;
    cin >> N;
    Graph G(N);
    vector<int> A(N-1), B(N-1);
    for (int i = 0; i < N-1; ++i) {
        cin >> A[i] >> B[i];
        --A[i], --B[i];
        G[A[i]].push_back(B[i]);
        G[B[i]].push_back(A[i]);
    }

    // DFS (根付き木にするのと、累積和をとるのを使い回す)
    int root = 0;
    vector<int> par(N, -1); // par[v]: 頂点 v の親
    vector<long long> add(N, 0);
    auto dfs = [&](auto self, int v, int p) -> void {
        par[v] = p;
        if (p != -1) add[v] += add[p];
        for (auto nv: G[v]) {
            if (nv == p) continue;
            self(self, nv, v);
        }
    };
    dfs(dfs, root, -1);

    // クエリ処理
    long long offset = 0;
    int Q;
    cin >> Q;
    while (Q--) {
        int type, id, v;
        cin >> type >> id >> v;
        --id;
        
        int a = A[id], b = B[id];
        if (type == 1) swap(a, b);
        
        if (par[b] == a) add[b] += v;
        else  add[a] -= v, offset += v;
    }
    
    // 累積和をとる
    dfs(dfs, root, -1);
    for (auto v: add) cout << v+offset << endl;    
}