AtCoder AGC 027 D - Modulo Matrix (赤色, 1100 点)

悔しい...

問題へのリンク

問題概要

整数 が与えらる。以下の条件を満たすような 行列 a を 1 つ構築せよ:

• 各要素の値は 以上 以下
• ある正の整数 が存在して、行列の上下左右に隣接する 2 数 をどこから取り出しても、max() を min() で割ったあまりは となる

制約

• 

考えたこと

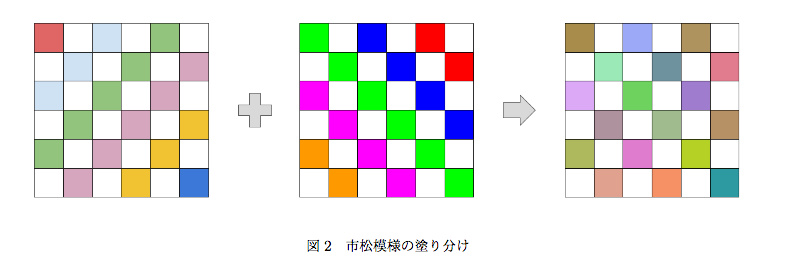
とりあえず下図のように市松模様に塗って、黒い部分に数字を当てはめて、白い部分は「上下左右の黒部分の最小公倍数 + 1」を割り当てればいいと思った。

ただし、テキトーにやると におさまらない。例えば、黒い部分は 125000 個あるのでテキトーにやると白いところの値は最悪 的な値になってしまう。

そこで、黒いところ同士がいい感じに公約数をもつ感じにすればよさそう。そしてこんな感じのを考えていた:

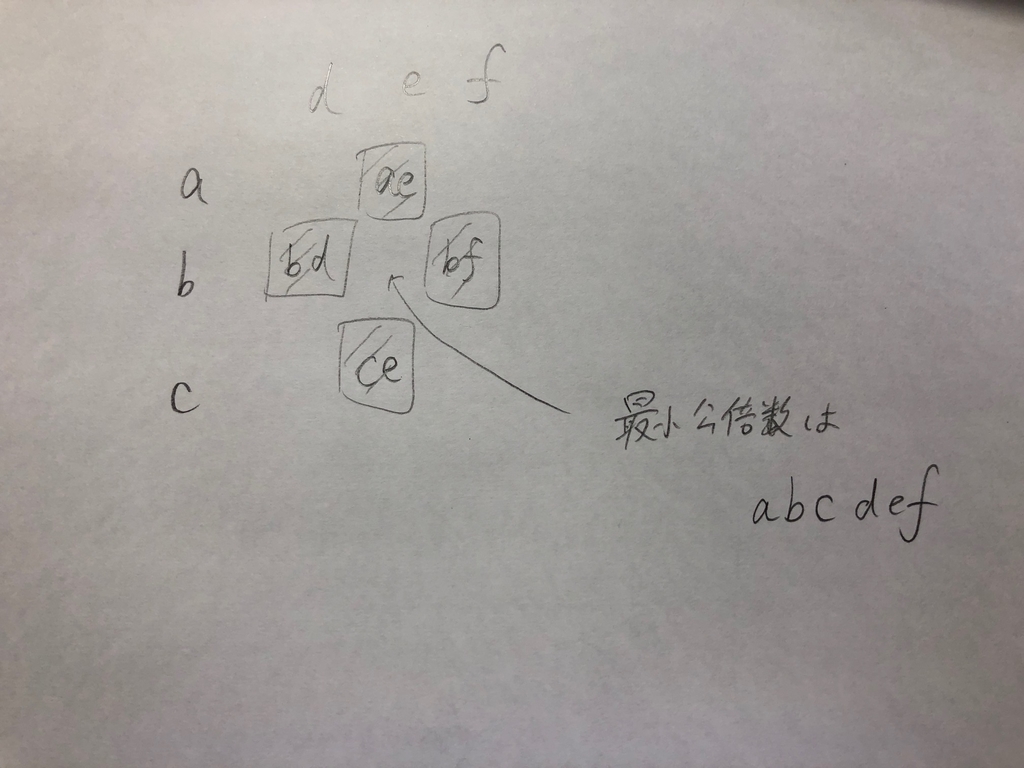
注意点として、a とか d といった値は素数にする必要がある。なぜならここを合成数にしてしまうと異なる黒マスの数字が被ってしまう恐れがある。そうすると 1000 個目の素数は 7919 なので、これを 6 個掛け合わせると、やはり を超えてしまう。。。ここで詰まっていた。

そして解説見て、この a とか d とかを掛け合わせる方向を (editorial にあった図) のように斜め掛けすればよかった。こうすると、黒い部分の数は

• 

みたいな感じになるので、最小公倍数は となって 7919 くらいの数を 4 つ掛け合わせた感じになる。これでギリギリ におさまる。

#include <iostream>
#include <vector>
using namespace std;

int dx[4] = {1, 0, -1, 0};
int dy[4] = {0, 1, 0, -1};

const int MAX = 10010;      // 素数判定する最大の数
bool IsPrime[MAX];
vector<int> Era(int n = MAX) {
    vector<int> res;
    IsPrime[0] = false; IsPrime[1] = false;
    for (int i = 2; i < n; ++i) IsPrime[i] = true;
    for (int i = 2; i < n; ++i) {
        if (IsPrime[i]) {
            res.push_back(i);
            for (int j = i*2; j < n; j += i) IsPrime[j] = false;
        }
    }
    return res;
}

long long GCD(long long a, long long b) {
    if (b == 0) return a;
    else return GCD(b, a % b);
}

long long LCM(long long a, long long b) {
    long long g = GCD(a, b);
    return a / g * b;
}

int main() {
    int N; cin >> N;
    vector<vector<long long> > res(N, vector<long long>(N, 0));
    vector<int> primes = Era();
    for (int wa = 0; wa <= N*2; wa += 2) {
        for (int sa = -N/2*2; sa <= N/2*2; sa += 2) {
            if ((wa + sa) & 1) continue;
            int i = (wa + sa) / 2;
            int j = (wa - sa) / 2;
            if (i < 0 || i >= N || j < 0 || j >= N) continue;
            if ((i + j) & 1) continue;
            res[i][j] = primes[wa/2] * primes[(sa + N/2*2)/2 + N];
        }
    }
    for (int i = 0; i < N; ++i) {
        for (int j = 0; j < N; ++j) {
            if ((i + j) % 2 == 0) continue;
            long long L = 1;
            for (int k = 0; k < 4; ++k) {
                int ni = i + dx[k], nj = j + dy[k];
                if (ni < 0 || ni >= N || nj < 0 || nj >= N) continue;
                L = LCM(L, res[ni][nj]);
            }
            res[i][j] = L + 1;
        }
    }
    if (N == 2) res[0][1] = res[1][0]*2-1;
    for (int i = 0; i < N; ++i) {
        for (int j = 0; j < N; ++j) {
            cout << res[i][j] << " ";
        }
        cout << endl;
    }
}