こういう系すごく楽しいよね
問題へのリンク
問題概要
頂点数  、辺数
、辺数  の重み付き有向単純グラフ
の重み付き有向単純グラフ  が与えられる。
が与えられる。
このグラフ上で次の条件を満たすパス (同じ頂点を二度通らないものに限る) が存在するかどうかを判定し、そのようなパスの重みの最小値を求めよ。ただし、長さ 0 のパスも重み 0 のパスとみなすことにする。
- パス上の辺の向きをすべて flip したときに、グラフ全体が強連結となる
制約
考えたこと
強連結性を考える問題なので、まずは強連結成分分解してみる。そして例によって、まずは必要条件を挙げて行ってみる (ダメなケースを列挙していく)。ここで、強連結成分分解したときの各強連結成分を縮約して得られるグラフを  とする。
とする。
 の source が 2 個以上あるときはダメ
の source が 2 個以上あるときはダメ の sink が 2 個以上あるときはダメ
の sink が 2 個以上あるときはダメ
ということがまずは考えられる。この先がかなり間違いやすくて怖いところ (僕も間違えた)。一応の正解は、以下の判定方法。
- 元のグラフ
 上で、source にある頂点群から、sink にある頂点群への最大フローの大きさが 2 以上であることが必要
上で、source にある頂点群から、sink にある頂点群への最大フローの大きさが 2 以上であることが必要
- 逆にこのとき、source にある頂点群から sink にある頂点群への最短パスを P とするとき、P を反転すれば強連結となる
なお、この判定方法の代わりに「元のグラフ  上で source にある頂点群から sink にある頂点群への最短パスを求めて、それを flip して実際に強連結となれば可能」という風に判定しても OK。
上で source にある頂点群から sink にある頂点群への最短パスを求めて、それを flip して実際に強連結となれば可能」という風に判定しても OK。
フローが 2 以上であることが必要であることの証明
source の頂点群から sink の頂点群へのフローが 1 のときは、カット S, T を考えたときに、S から T へと入る辺は 1 本しかないので、そこを flip してしまうと明らかに強連結とはならない。よってフローが 2 以上であることが必要と言える。
P を反転すれば強連結となることの証明
フローが 2 以上であるならば、P に対する増加パス Q が存在する。ここで P を反転したとする (P' とする)。なおこのとき P の最短性から、P の flip 操作によって、source や sink が強連結成分であることが崩れないことに注意する。
この P を反転したグラフ上で、任意の頂点 u から任意の頂点 v へと到達できることを示そう。まず、u から source にも sink にも到達できることを示す。元のグラフでは u から sink へ到達できるパス R が存在するはずである。そのパス R 上に P' の辺がなければ sink へ到達することができて、P' をたどって source にも到達できる。パス R 上に P' 上の頂点があるならば、そこから P' に沿って source に到達できるし、そこからパス Q に沿って sink に到達できる。次に、source や sink から任意の頂点 v へ到達できることを示す。元のグラフで source から頂点 v へ到達するパス S を考える。パス S 上にパス P' 上の頂点があるとき、そのうち最も v に近い頂点には sink から P' に沿って到達できて、そこから S に沿って v へと到達できる。以上から、source 群から sink 群へのフローが 2 以上であるとき、source にある頂点群から sink にある頂点群への最短パス P' を flip したときに強連結になることが示された。
嘘判定:G' の source から sink へのフローが 2 以上
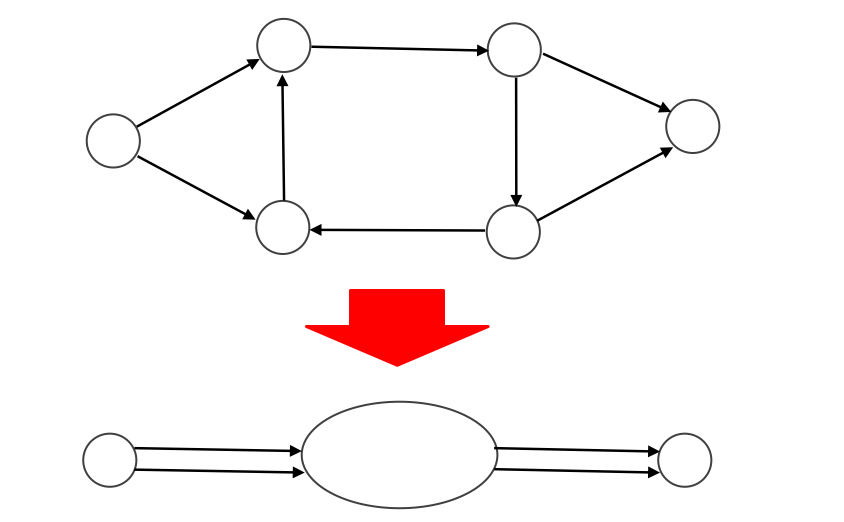
下図のような反例がある。縮約後の G' ではフローが 2 以上だが、条件を満たすパスは存在しない。
まとめ
- 強連結成分分解する
- 強連結成分がただ 1 つならば、答えは 0
- そうでないとき、source 成分が複数個、sink 成分が複数個のときはダメ
- 元のグラフ上で source の頂点群から sink の頂点群への最大フロー値が 2 以上でなければダメ
以上の条件を満たすとき、source の頂点群から sink の頂点群への最短パスを求めれば、それが答えとなる。計算量は (フローアルゴリズムで 2 本とれた時点で打ち切って OK)。
(フローアルゴリズムで 2 本とれた時点で打ち切って OK)。
コード
#include <bits/stdc++.h>
using namespace std;
template<class T> inline bool chmax(T& a, T b) { if (a < b) { a = b; return 1; } return 0; }
template<class T> inline bool chmin(T& a, T b) { if (a > b) { a = b; return 1; } return 0; }
struct SCC {
using Edge = int;
using SGraph = vector<vector<Edge>>;
SGraph G, rG;
vector<vector<int>> scc;
vector<int> cmp;
SGraph dag;
SCC(int N) : G(N), rG(N) {}
void addedge(int u, int v) {
G[u].push_back(v);
rG[v].push_back(u);
}
vector<bool> seen;
vector<int> vs, rvs;
void dfs(int v) {
seen[v] = true;
for (auto e : G[v]) if (!seen[e]) dfs(e);
vs.push_back(v);
}
void rdfs(int v, int k) {
seen[v] = true;
cmp[v] = k;
for (auto e : rG[v]) if (!seen[e]) rdfs(e, k);
rvs.push_back(v);
}
set<pair<int,int>> newEdges;
void reconstruct() {
int N = (int)G.size();
int dV = (int)scc.size();
dag.assign(dV, vector<Edge>());
newEdges.clear();
for (int i = 0; i < N; ++i) {
int u = cmp[i];
for (auto e : G[i]) {
int v = cmp[e];
if (u == v) continue;
if (!newEdges.count({u, v})) {
dag[u].push_back(v);
newEdges.insert({u, v});
}
}
}
}
void solve() {
int N = (int)G.size();
seen.assign(N, false);
vs.clear();
for (int v = 0; v < N; ++v) if (!seen[v]) dfs(v);
int k = 0;
scc.clear();
cmp.assign(N, -1);
seen.assign(N, false);
for (int i = N - 1; i >= 0; --i) {
if (!seen[vs[i]]) {
rvs.clear();
rdfs(vs[i], k++);
scc.push_back(rvs);
}
}
reconstruct();
}
};
template<class FLOWTYPE> struct Edge {
int rev, from, to;
FLOWTYPE cap, icap;
Edge(int r, int f, int t, FLOWTYPE c) : rev(r), from(f), to(t), cap(c), icap(c) {}
friend ostream& operator << (ostream& s, const Edge& E) {
if (E.cap > 0) return s << E.from << "->" << E.to << '(' << E.cap << ')';
else return s;
}
};
template<class FLOWTYPE> struct Graph {
vector<vector<Edge<FLOWTYPE> > > list;
Graph(int n = 0) : list(n) { }
void init(int n = 0) { list.clear(); list.resize(n); }
void reset() { for (int i = 0; i < (int)list.size(); ++i) for (int j = 0; j < list[i].size(); ++j) list[i][j].cap = list[i][j].icap; }
inline vector<Edge<FLOWTYPE> >& operator [] (int i) { return list[i]; }
inline const size_t size() const { return list.size(); }
inline Edge<FLOWTYPE> &redge(Edge<FLOWTYPE> e) {
if (e.from != e.to) return list[e.to][e.rev];
else return list[e.to][e.rev + 1];
}
void addedge(int from, int to, FLOWTYPE cap) {
list[from].push_back(Edge<FLOWTYPE>((int)list[to].size(), from, to, cap));
list[to].push_back(Edge<FLOWTYPE>((int)list[from].size() - 1, to, from, 0));
}
void add_undirected_edge(int from, int to, FLOWTYPE cap) {
list[from].push_back(Edge<FLOWTYPE>((int)list[to].size(), from, to, cap));
list[to].push_back(Edge<FLOWTYPE>((int)list[from].size() - 1, to, from, cap));
}
};
template<class FLOWTYPE> struct Dinic {
const FLOWTYPE INF = 1<<30;
vector<int> level, iter;
Dinic() { }
void dibfs(Graph<FLOWTYPE> &G, int s) {
level.assign((int)G.size(), -1);
level[s] = 0;
queue<int> que;
que.push(s);
while (!que.empty()) {
int v = que.front();
que.pop();
for (int i = 0; i < G[v].size(); ++i) {
Edge<FLOWTYPE> &e = G[v][i];
if (level[e.to] < 0 && e.cap > 0) {
level[e.to] = level[v] + 1;
que.push(e.to);
}
}
}
}
FLOWTYPE didfs(Graph<FLOWTYPE> &G, int v, int t, FLOWTYPE f) {
if (v == t) return f;
for (int &i = iter[v]; i < G[v].size(); ++i) {
Edge<FLOWTYPE> &e = G[v][i], &re = G.redge(e);
if (level[v] < level[e.to] && e.cap > 0) {
FLOWTYPE d = didfs(G, e.to, t, min(f, e.cap));
if (d > 0) {
e.cap -= d;
re.cap += d;
return d;
}
}
}
return 0;
}
FLOWTYPE solve(Graph<FLOWTYPE> &G, int s, int t) {
level.assign((int)G.size(), -1); iter.assign((int)G.size(), 0);
FLOWTYPE res = 0;
while (true) {
dibfs(G, s);
if (level[t] < 0) return res;
for (int i = 0; i < (int)iter.size(); ++i) iter[i] = 0;
FLOWTYPE flow = 0;
while ((flow = didfs(G, s, t, INF)) > 0) {
res += flow;
}
}
}
};
const int INF = 1<<29;
int solve() {
int N, M;
cin >> N >> M;
SCC scc(N);
Graph<int> fG(N+2);
int s = N, t = N+1;
for (int i = 0; i < M; ++i) {
int u, v;
cin >> u >> v;
--u, --v;
scc.addedge(u, v);
fG.addedge(u, v, 1);
}
scc.solve();
int siz = scc.scc.size();
if (siz == 1) return 0;
set<int> source, sink;
for (int k = 0; k < siz; ++k) source.insert(k), sink.insert(k);
for (int v = 0; v < siz; ++v) {
for (auto e : scc.dag[v]) {
source.erase(e);
sink.erase(v);
}
}
if (source.size() > 1) return -1;
if (sink.size() > 1) return -1;
vector<int> S = scc.scc[*source.begin()], T = scc.scc[*sink.begin()];
for (auto v : S) fG.addedge(s, v, INF);
for (auto v : T) fG.addedge(v, t, INF);
Dinic<int> din;
int maxflow = din.solve(fG, s, t);
if (maxflow < 2) return -1;
auto G = scc.G;
vector<int> dist(N, -1);
queue<int> que;
for (auto v : S) dist[v] = 0, que.push(v);
while (!que.empty()) {
int v = que.front();
que.pop();
for (auto e : G[v]) {
if (dist[e] == -1) {
dist[e] = dist[v] + 1;
que.push(e);
}
}
}
int res = INF;
for (auto v : T) chmin(res, dist[v]);
return res;
}
int main() {
cout << solve() << endl;
}
の番号を振られた
個の頂点があります。 最初、これらを繋ぐ辺はありません。 あなたはいくつかの辺を追加してこのグラフを連結にしたいと思いました。
と
を繋ぐ辺を追加するには
のコストがかかります。 このグラフを連結にするように辺を追加するとき、かかるコストの和の最小値を求めてください。
となる。よって全体の計算量は
。
