問題概要

$N$ 以下の正整数からなる長さ $M$ の数列 $A_{1}, A_{2}, \dots, A_{M}$ 、 $B_{1}, B_{2}, \dots, B_{M}$ が与えられる。これらの数列の組が次の条件を満たすかどうかを判定せよ。

0 と 1 のみからなる長さ $N$ の数列 $X_{1}, X_{2}, \dots, X_{N}$ が存在して
各 $i = 1, 2, \dots, M$ について、 $X_{A_{i}} \neq X_{B_{i}}$ が成り立つ

制約

$1 \le N, M \le 2 \times 10^{5}$

考えたこと

グラフの問題として考えてみよう。

数列 $X_{1}, X_{2}, \dots, X_{N}$ の値を定めるというのは、 $N$ 個の頂点に対して 0 と 1 という値を割り当てることと捉え直せる。このとき、たとえば $A_{0} = 1$ 、 $B_{0} = 2$ であるというのは、このグラフの頂点 1 と頂点 2 に割り当てる値を変えなければならないことを意味する。

このような観察から、この問題が次の問題に言い換えられることに気づく。

頂点数 $N$ 、辺数 $M$ のグラフが与えられる。

各頂点を黒色または白色に塗っていく方法であって、どの辺の両端点も色が異なるような方法が存在するかを判定せよ。

つまり、二部グラフ判定だといえる。二部グラフとは、下図のように、グラフの各頂点を黒色または白色に塗る方法であって、黒色頂点同士や白色頂点同士には辺が張られないようにできるグラフのことを言う。

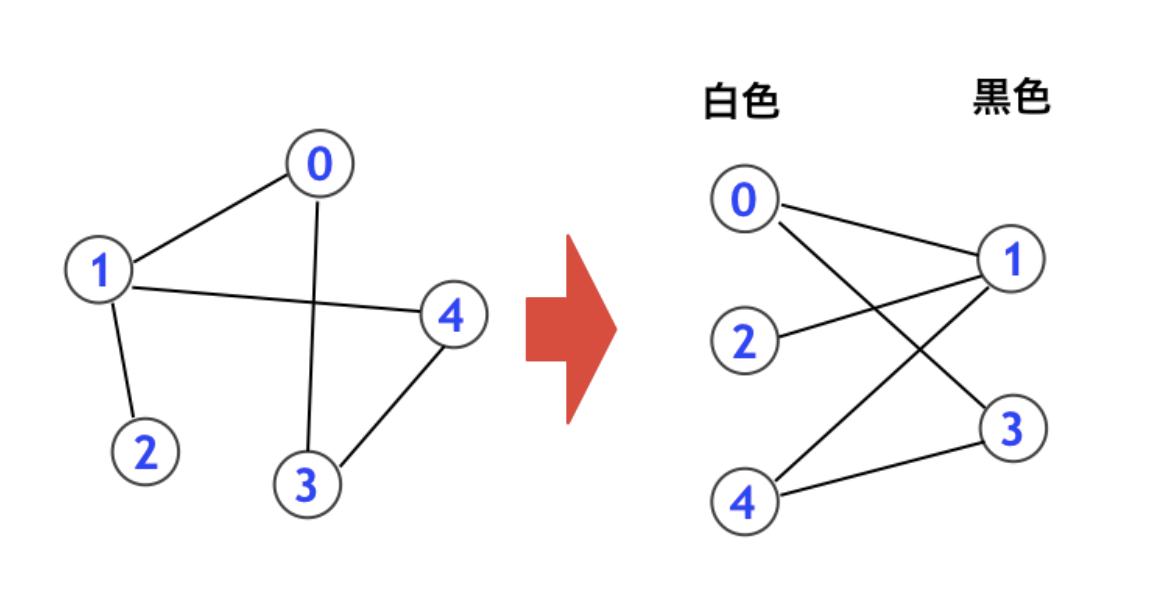
二部グラフ判定の解説は、けんちょん本 13 章にも書いたし、他にも次の Qiita 記事にも書いた。計算量は $O(N + M)$ となる。

DFS による方法

qiita.com

BFS による方法

qiita.com

コード

ここでは DFS で通した。

#include <bits/stdc++.h>
using namespace std;


// 二部グラフ判定
using Graph = vector<vector<int>>;
bool dfs(const Graph &G, int v, int c, vector<int> &color) {
    color[v] = c;
    for (auto v2 : G[v]) {
        if (color[v2] == 0) {
            if (!dfs(G, v2, -c, color)) return false;
        } else if (color[v2] != -c) return false;
    }
    return true;
}

bool is_bipartite(const Graph &G) {
    int N = (int)G.size();
    vector<int> color(N, 0);
    for (int v = 0; v < N; ++v) {
        if (color[v] != 0) continue;
        if (!dfs(G, v, 1, color)) return false;
    }
    return true;
}


void ABC_327_D() {
    int N, M;
    cin >> N >> M;
    vector<int> A(M), B(M);
    for (int i = 0; i < M; ++i) cin >> A[i], --A[i];
    for (int i = 0; i < M; ++i) cin >> B[i], --B[i];
    
    vector<vector<int>> G(N);
    for (int i = 0; i < M; ++i) {
        G[A[i]].push_back(B[i]);
        G[B[i]].push_back(A[i]);
    }
    cout << (is_bipartite(G) ? "Yes" : "No") << endl;
}


int main() {
    ABC_327_D();
}