AtCoder AGC 006 D - Median Pyramid Hard (赤色, 1300 点)

一目見て、データ構造げーかな...と思ってしまった。そういう先入観を持つと危ない。実際は好みな考察で解ける問題だった。

問題へのリンク

問題概要

正の整数 と からなる順列が与えられる。いま、この順列を下図左のようにピラミッドの最底辺に書き込む。各マスに対して

• そのマスの直下にある 3 マスの中央値を書き込む

という操作を下から順に行ったとき、頂上に何が書き込まれるのかを求めよ。

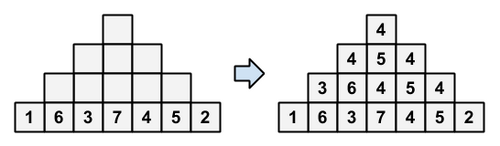
制約

• 

考えたこと

1300 点でありながら、まさかの「〜を求めよ」系！！！！！

• 〜した結果が〜となるものが存在するかを判定せよ
• 〜した結果が〜となるようなものを求めよ
• 〜した結果が〜となるものを数え上げよ

という問題が高難易度帯に溢れかえる中、まさかの素直な「〜した結果がどうなるかを求めよ」という問題。

上記のようないわば「逆」を求めるような問題は、そもそも計算量を度外視しても多項式時間で求めるだけでも難しく、そこからさらに計算量を落とすステップを要求するものが多い。

それに対して今回の問題は、計算量度外視でいいなら最初から自明になっている。つまり愚直にやれば でできる。つまりは計算量を落とすことのみが本質の問題。それで 1300 点ってやばそう。。。

で、僕は一目見て、データ構造ゲーか、、、と思ってしまった。なんか、順列の何かを上手くデータ構造で管理して高速に求めていくような。。。でも思い込みはよくない。

とりあえず手を動かしてみる

この手の問題で、まずは手を動かしてみるのはそれはそう。
試しに、 をやってみると

    4
  3 4 4
3 1 4 5 2

となる。なんか 4 がそのまま上に行った格好だ。 をやってみる。

      4
    5 4 4
  5 5 4 3 4
2 7 5 3 4 1 6

となる。うーんぐちゃぐちゃ。でも、上の 2 例を見ていて、最底辺の値がそのまま真上にズドーンと来ている部分があることがわかる。例えば、1 個目の (1, 4, 5) のところは 4 が上まで伸びてるし、2 個目の (7, 5, 3) のところは 5 が上まで伸びている。

一般に (大, 中, 小) や (小, 中, 大) なやつは、中がそのまんま真上までずっと伸びることが示せる。

1 個要素を固定して考えてみる

この手の「全体に対して操作を順にしていく」問題では、「個別の要素の動きに着目してみる」というのは有効だと思う。

今回、左右に「自分より大きいやつ」と「自分より小さいやつ」に挟まれてるやつはそのまんま真っ直ぐ上まで行くことがわかった。それじゃあ、一般に、順列を「自分より大きいやつ」を o、「自分より小さいやつ」を x と表して様子を見てみよう (自分を s にしている)。例えばこんな感じ。

          o
        o o s
      o o s o s
    o o s o s o s
  o o x o s o s o x
o o x o x o s o x o x

このことから

---

数値 s を固定して、最底辺の「s」「s より大きい」「s より小さい」だけ決まっていれば、頂上が「s」「s より大きい」「s より小さい」のいずれになるかが決まる

---

ということがわかる。よって問題となるのは「頂上が s になるような s を見つける」という問題になることがわかる。

二分探索へ

このままだと s を全通り試す感じになる...が、ちょっと考えると単調性が見えて二分探索が使える形になる！！！！！

例えば s として設定する値を 1, 2, 3, ..., 2N-1 と大きくすると、頂上の値は

o, o, o, ..., o, s, x, x, ..., x

という感じになる。よく見ると単調性があるのでピッタリのところを二分探索で見つける形で行ける！！！

あと、s も o として扱ってしまうことにして、o と x だけで考えていくことにする。

個々の判定を高速化

しかしこれでもまだ、o, x, s の動きを愚直にシミュレートしていては、毎回 の計算量がかかってしまい、合計で とむしろ悪化してしまう。

そこで、初期並び

o, o, x, o, x, x, o, o, o

から頂上を高速に予測する必要がある。実は既にこの予測技術を我々は身につけていて、

• oo や xx のように o や x が連続している箇所があったらそこから上はすべて oo や xx が続いていくことになる
• oo や xx は徐々に左右に侵食していく
• ox や xo は左右にある oo や xx に侵食されるまでは、反転を繰り返す

という感じになる。なので

• 真ん中から左右に見て、「左側の最初に oo か xx になるところ」と「右側の最初に oo か xx になるところ」のどちらが近いかを見て、近い方の o か x かで決まる (このとき両端のさらに左右には同じ色があるとしてよい)

という風に解くことができる。

#include <iostream>
#include <vector>
#include <deque>
#include <algorithm>
using namespace std;

bool solve(const vector<int> &a, int x) {
    deque<int> b;
    for (int i = 0; i < a.size(); ++i) {
        if (a[i] >= x) b.push_back(1);
        else b.push_back(0);
    }
    b.push_front(b[0]);
    b.push_back(b.back());
    
    int mid = b.size() / 2;
    int left, right;
    for (int i = mid - 1; i >= 0; --i) {
        if (b[i] == b[i+1]) {
            left = i;
            break;
        }
    }
    for (int i = mid + 1; i  < b.size(); ++i) {
        if (b[i-1] == b[i]) {
            right = i;
            break;
        }
    }
    if (right - mid >= mid - left) return b[left];
    else return b[right];
}

int main() {
    int N, K; cin >> N;
    vector<int> a(N * 2 - 1);
    for (int i = 0; i < N * 2 - 1; ++i) cin >> a[i];

    int low = 0, high = N*2;
    while (high - low > 1) {
        int mid = (high + low) / 2;
        if (solve(a, mid)) low = mid;
        else high = mid;
    }
    cout << low << endl;
}