いわゆる本当に最初の入門という感じの DP だね。
問題概要
段の階段があって、現在は 0 段目にいる。
高橋君は一歩で 1 段か 2 段上がることができる。ただし 段目は壊れていて、そこに足を踏み入れることはできない。
高橋君が 0 段目から 段目までたどり着くまでの移動方法は何通りあるか、1000000007 で割ったあまりを求めよ。
制約
壊れているところがなかったら
もしかしたら高校時代に似たような問題を解いたことのある方も多いかもしれない。すなわち「どこも壊れていないバージョン」なら解いたことある方も多いかもしれない。
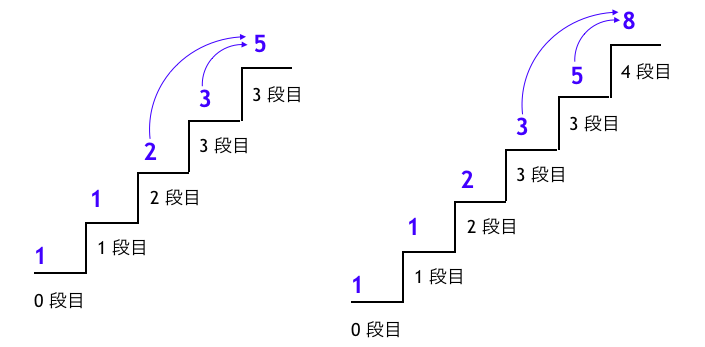
下図のように
- 0 段目は「なにもしない」という 1 通り
- 1 段目は「0 段目から 1 段のぼり」という 1 通り
- 2 段目は、その直前がどうだったかが以下の 2 つの場合があって、それらを合計して 2 通り
- 直前が 0 段目:1 通り
- 直前が 1 段目:1 通り
- 3 段目は、その直前がどうだったかが以下の 2 つの場合があって、それらを合計して 3 通り
- 直前が 1 段目:1 通り
- 直前が 2 段目:2 通り
- 4 段目は、その直前がどうだったかが以下の 2 つの場合があって、それらを合計して 5 通り
- 直前が 2 段目:2 通り
- 直前が 3 段目:3 通り
- 5 段目は、その直前がどうだったかが以下の 2 つの場合があって、それらを合計して 8 通り
- 直前が 3 段目:3 通り
- 直前が 4 段目:5 通り
という感じになる。

これを漸化式で表すと、 段目まで登る方法の数を
通りとすると、
段目から来る:
通り
段目から来る:
通り
となるので、
という漸化式がたつことになる。これはフィボナッチ数列の漸化式でもある。
さて、ここでやっているのはまさに dp そのもので、
- dp[ v ] := v 段目まで登る方法の数
とすると、v 段目まで登る方法は
- v-2 段目から来る:dp[ v - 2 ] 通り
- v-1 段目から来る:dp[ v - 1 ] 通り
あるので、結局
- dp[ v ] = dp[ v - 1 ] + dp[ v - 2 ]
という式が立つことになる。こうしてみると、DP は漸化式だという立場の気持ちもよくわかる。実装もシンプルに
dp[0] = 1; dp[1] = 1; for (int i = 2; i <= n; ++i) { dp[i] = dp[i-1] + dp[i-2]; }
という雰囲気で書くことができる (ここでは 1000000007 で割ることは無視してる)。
壊れたところもある
壊れたところがあっても、実はほとんど難易度は変わらなくて、同じように
- dp[ v ] = v 段目までのぼる場合の数
として、v 段目までのぼる方法を
- v-2 段目から来る:dp[ v - 2 ] 通り
- v-1 段目から来る:dp[ v - 1 ] 通り
という感じで場合分けしていたところを、
- v-2 段目から来る:dp[ v - 2 ] 通り (ただし v-2 段目が壊れていたらなし)
- v-1 段目から来る:dp[ v - 1 ] 通り (ただし v-1 段目が壊れていたらなし)
とするだけである。詳しくは実装をみるとわかると思う (if 文で分岐してる)。あとは 1000000007 で割る というところに注意。
#include <iostream> #include <vector> using namespace std; const int MOD = 1000000007; int N, M; vector<bool> issafe; // issafe[v] := v が壊れていないかどうか int main() { cin >> N >> M; issafe.assign(N+1, true); for (int i = 0; i < M; ++i) { int a; cin >> a; issafe[a] = false; // a 段目は壊れてる } // DP テーブル vector<int> dp(N+1, 0); // 各段について 0 で初期化しておく // 初期条件 dp[0] = 1; if (issafe[1]) dp[1] = 1; // ループ for (int n = 2; n <= N; ++n) { if (issafe[n-1]) dp[n] += dp[n-1]; // n-1 段目が安全なら if (issafe[n-2]) dp[n] += dp[n-2]; // n-2 段目が安全なら dp[n] %= MOD; // 1000000007 で割る } cout << dp[N] << endl; }