文字列の連続した部分文字列を数え上げるのは Suffix Array の典型問題。それを少し応用した面白い問題!
問題概要
英小文字からなる 2 つの文字列  が与えられる。次の条件を満たす文字列の個数を求めよ。
が与えられる。次の条件を満たす文字列の個数を求めよ。
 中に連続した部分文字列として含まれる
中に連続した部分文字列として含まれる 中に連続した部分文字列として含まれない
中に連続した部分文字列として含まれない
制約
考えたこと
前提となる問題がこちら。
drken1215.hatenablog.com
さて、2 つの文字列にまたがる文字列検索について考える問題では、
 =
=  + "?" +
+ "?" + 
というように、 を連結させた文字列について Suffix Array を求めるのは常套手段。
を連結させた文字列について Suffix Array を求めるのは常套手段。
たとえば、 = "abcab"、
= "abcab"、 = "bcab" のとき、接尾辞配列は次のようになる。
= "bcab" のとき、接尾辞配列は次のようになる。
0: 10,
1: 5, ?bcab
2: 8, ab
3: 3, ab?bcab
4: 0, abcab?bcab
5: 9, b
6: 4, b?bcab
7: 6, bcab
8: 1, bcab?bcab
9: 7, cab
10: 2, cab?bcab
このうち、"?" を含む suffix たち (それ以外は文字列  に関するものなのでスキップ) について、次のルールで集計していくことにする。
に関するものなのでスキップ) について、次のルールで集計していくことにする。
今考えている suffix の prefix として考えられる文字列のうち
- "?" を含むものは除外する
- Suffix Array のより後方にある suffix の prefix となり得るものは除外する
- Suffix Array のより前方にある suffix のうち、index が B 側にあるものの prefix となり得るものも除外する
具体的には、
- 1 を考慮すると、個数は
add = N - sa[i] と表せる
- 2, 3 をそれぞれ考慮して、その最大値を
sub として、add から sub を引くことにする
- 2 を考慮すると、
chmax(sub, lcp[i]) と表せる
- 3 を考慮すると、Suffix Array において直前の B 由来の index を
prev として、chmax(sub, lcp(sa[i], prev)) と表せる
そうして、add - sub の値の総和をとったものが答えとなる。
全体として、 の計算量で求められる。
の計算量で求められる。
コード
#include <bits/stdc++.h>
using namespace std;
using pint = pair<int, int>;
using pll = pair<long long, long long>;
template<class T> inline bool chmax(T& a, T b) { if (a < b) { a = b; return 1; } return 0; }
template<class T> inline bool chmin(T& a, T b) { if (a > b) { a = b; return 1; } return 0; }
#define REP(i, n) for (long long i = 0; i < (long long)(n); ++i)
#define REP2(i, a, b) for (long long i = a; i < (long long)(b); ++i)
#define COUT(x) cout << #x << " = " << (x) << " (L" << __LINE__ << ")" << endl
template<class T1, class T2> ostream& operator << (ostream &s, pair<T1,T2> P)
{ return s << '<' << P.first << ", " << P.second << '>'; }
template<class T> ostream& operator << (ostream &s, vector<T> P)
{ for (int i = 0; i < P.size(); ++i) { if (i > 0) { s << " "; } s << P[i]; } return s; }
template<class T> ostream& operator << (ostream &s, deque<T> P)
{ for (int i = 0; i < P.size(); ++i) { if (i > 0) { s << " "; } s << P[i]; } return s; }
template<class T> ostream& operator << (ostream &s, vector<vector<T> > P)
{ for (int i = 0; i < P.size(); ++i) { s << endl << P[i]; } return s << endl; }
template<class T> ostream& operator << (ostream &s, set<T> P)
{ for(auto it : P) { s << "<" << it << "> "; } return s; }
template<class T1, class T2> ostream& operator << (ostream &s, map<T1,T2> P)
{ for(auto it : P) { s << "<" << it.first << "->" << it.second << "> "; } return s; }
template<class MeetSemiLattice> struct SparseTable {
vector<vector<MeetSemiLattice> > dat;
vector<int> height;
SparseTable() { }
SparseTable(const vector<MeetSemiLattice> &vec) { init(vec); }
void init(const vector<MeetSemiLattice> &vec) {
int n = (int)vec.size(), h = 0;
while ((1<<h) < n) ++h;
dat.assign(h, vector<MeetSemiLattice>(1<<h));
height.assign(n+1, 0);
for (int i = 2; i <= n; i++) height[i] = height[i>>1]+1;
for (int i = 0; i < n; ++i) dat[0][i] = vec[i];
for (int i = 1; i < h; ++i)
for (int j = 0; j < n; ++j)
dat[i][j] = min(dat[i-1][j], dat[i-1][min(j+(1<<(i-1)),n-1)]);
}
MeetSemiLattice get(int a, int b) {
return min(dat[height[b-a]][a], dat[height[b-a]][b-(1<<height[b-a])]);
}
};
template<class Str> struct SuffixArray {
Str str;
vector<int> sa;
vector<int> rank;
vector<int> lcp;
SparseTable<int> st;
int& operator [] (int i) {
return sa[i];
}
vector<int> get_sa() { return sa; }
vector<int> get_rank() { return rank; }
vector<int> get_lcp() { return lcp; }
SuffixArray(const Str& str_) : str(str_) {
build_sa();
}
void init(const Str& str_) {
str = str_;
build_sa();
}
void build_sa() {
vector<int> s;
for (int i = 0; i < (int)str.size(); ++i) {
s.push_back(str[i] + 1);
}
s.push_back(0);
sa = sa_is(s);
calcLCP(s);
buildSparseTable();
}
vector<int> sa_is(vector<int> &s, int upper = 256) {
int N = (int)s.size();
if (N == 0) return {};
else if (N == 1) return {0};
else if (N == 2) {
if (s[0] < s[1]) return {0, 1};
else return {1, 0};
}
vector<int> isa(N);
vector<bool> ls(N, false);
for (int i = N - 2; i >= 0; --i) {
ls[i] = (s[i] == s[i + 1]) ? ls[i + 1] : (s[i] < s[i + 1]);
}
vector<int> sum_l(upper + 1, 0), sum_s(upper + 1, 0);
for (int i = 0; i < N; ++i) {
if (!ls[i]) ++sum_s[s[i]];
else ++sum_l[s[i] + 1];
}
for (int i = 0; i <= upper; ++i) {
sum_s[i] += sum_l[i];
if (i < upper) sum_l[i + 1] += sum_s[i];
}
auto induce = [&](const vector<int> &lms) -> void {
fill(isa.begin(), isa.end(), -1);
vector<int> buf(upper + 1);
copy(sum_s.begin(), sum_s.end(), buf.begin());
for (auto d: lms) {
if (d == N) continue;
isa[buf[s[d]]++] = d;
}
copy(sum_l.begin(), sum_l.end(), buf.begin());
isa[buf[s[N - 1]]++] = N - 1;
for (int i = 0; i < N; ++i) {
int v = isa[i];
if (v >= 1 && !ls[v - 1]) {
isa[buf[s[v - 1]]++] = v - 1;
}
}
copy(sum_l.begin(), sum_l.end(), buf.begin());
for (int i = N - 1; i >= 0; --i) {
int v = isa[i];
if (v >= 1 && ls[v - 1]) {
isa[--buf[s[v - 1] + 1]] = v - 1;
}
}
};
vector<int> lms, lms_map(N + 1, -1);
int M = 0;
for (int i = 1; i < N; ++i) {
if (!ls[i - 1] && ls[i]) {
lms_map[i] = M++;
}
}
lms.reserve(M);
for (int i = 1; i < N; ++i) {
if (!ls[i - 1] && ls[i]) {
lms.push_back(i);
}
}
induce(lms);
if (M) {
vector<int> lms2;
lms2.reserve(isa.size());
for (auto v: isa) {
if (lms_map[v] != -1) lms2.push_back(v);
}
int rec_upper = 0;
vector<int> rec_s(M);
rec_s[lms_map[lms2[0]]] = 0;
for (int i = 1; i < M; ++i) {
int l = lms2[i - 1], r = lms2[i];
int nl = (lms_map[l] + 1 < M) ? lms[lms_map[l] + 1] : N;
int nr = (lms_map[r] + 1 < M) ? lms[lms_map[r] + 1] : N;
bool same = true;
if (nl - l != nr - r) same = false;
else {
while (l < nl) {
if (s[l] != s[r]) break;
++l, ++r;
}
if (l == N || s[l] != s[r]) same = false;
}
if (!same) ++rec_upper;
rec_s[lms_map[lms2[i]]] = rec_upper;
}
auto rec_sa = sa_is(rec_s, rec_upper);
vector<int> sorted_lms(M);
for (int i = 0; i < M; ++i) {
sorted_lms[i] = lms[rec_sa[i]];
}
induce(sorted_lms);
}
return isa;
}
int lower_bound(const Str& T) {
int left = -1, right = sa.size();
while (right - left > 1) {
int mid = (left + right) / 2;
if (str.compare(sa[mid], string::npos, T) < 0)
left = mid;
else
right = mid;
}
return right;
}
int upper_bound(const Str& T) {
int left = -1, right = sa.size();
while (right - left > 1) {
int mid = (left + right) / 2;
if (str.compare(sa[mid], T.size(), T) <= 0)
left = mid;
else
right = mid;
}
return right;
}
bool is_contain(const Str& T) {
int lb = lower_bound(T);
if (lb >= sa.size()) return false;
return str.compare(sa[lb], T.size(), T) == 0;
}
void calcLCP(const vector<int> &s) {
int N = (int)s.size();
rank.assign(N, 0), lcp.assign(N, 0);
for (int i = 0; i < N; ++i) rank[sa[i]] = i;
int h = 0;
for (int i = 0; i < N - 1; ++i) {
int pi = sa[rank[i] - 1];
if (h > 0) --h;
for (; pi + h < N && i + h < N; ++h) {
if (s[pi + h] != s[i + h]) break;
}
lcp[rank[i] - 1] = h;
}
}
void buildSparseTable() {
st.init(lcp);
}
int getLCP(int a, int b) {
return st.get(min(rank[a], rank[b]), max(rank[a], rank[b]));
}
};
int main() {
string A, B;
cin >> A >> B;
int N = A.size(), M = B.size();
string S = A + "?" + B;
SuffixArray<string> suf(S);
vector<int> sa = suf.get_sa();
vector<int> lcp = suf.get_lcp();
long long res = 0;
int prev = -1;
for (int i = 0; i < sa.size(); ++i) {
if (sa[i] > N) {
prev = sa[i];
continue;
}
int add = N - sa[i];
int sub = 0;
if (i < lcp.size()) chmax(sub, lcp[i]);
if (prev > N) chmax(sub, suf.getLCP(sa[i], prev));
res += add - sub;
}
cout << res << endl;
}
、辺数
の単純な無向グラフが与えられます。頂点番号を
とします。
(
) の個数を答えてください。
を結ぶ辺が存在しない
を結ぶ辺を追加したグラフは二部グラフである
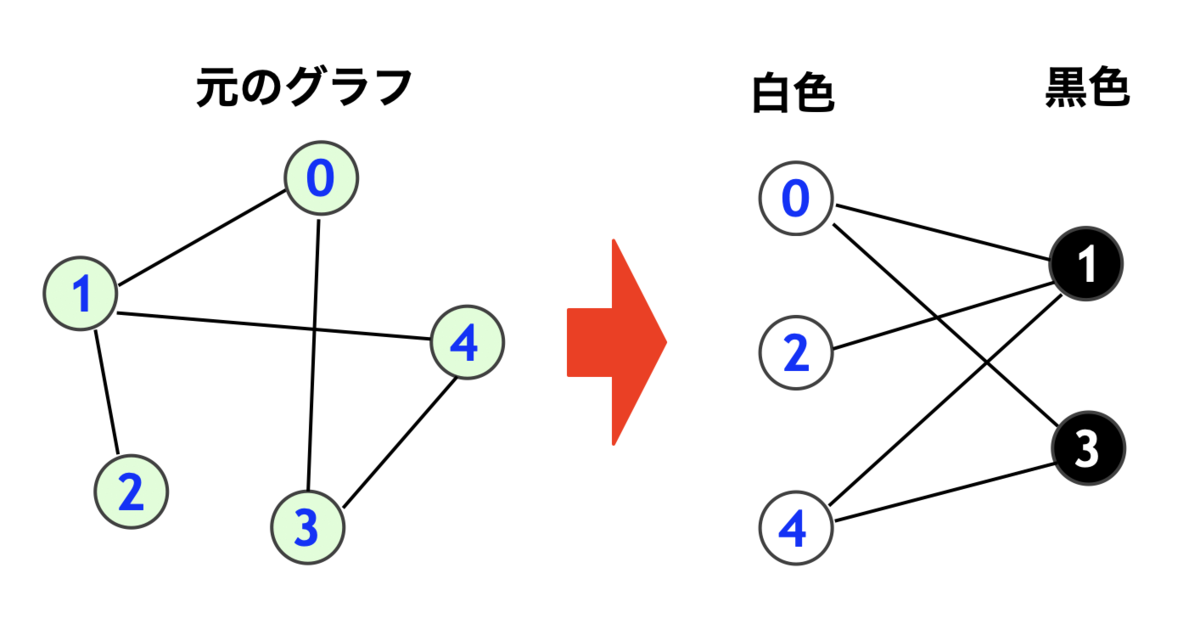
個
個
本
本の頂点組には辺を追加できる。なお、後述するように、実際には「連結成分ごとに
を求める」という作業は必要ない。

の値が変わってしまうのではないかということだ。
個」「黒色
個」というように
が入れ替わることはあっても、値が変わることはないのだ。

、黒色頂点の個数を
としたとき、結んではいけない辺の本数は
となる。