問題概要

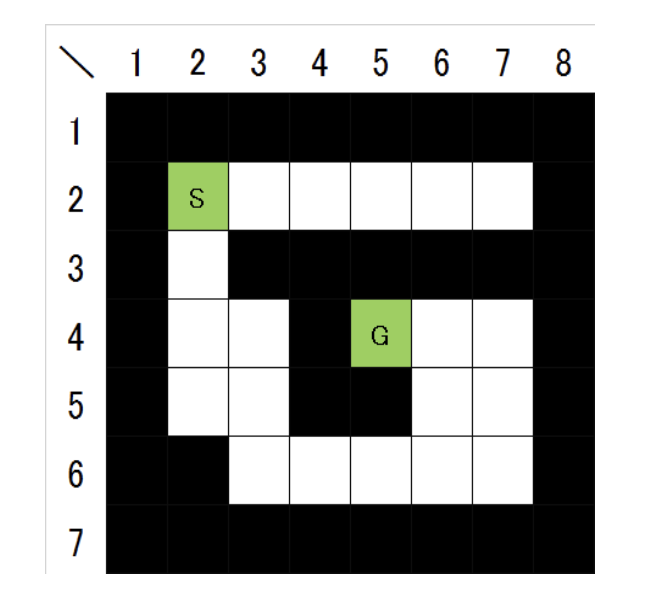
$R \times C$ のグリッドが与えられます。各マスは壁 (文字 '#')、通路 (文字 '.') のいずれかです。通路マスに入ることはできますが、壁マスに入ることはできません。

スタートマス (入力で与えられる) から出発して、上下左右のマスへの移動を繰り返して、通路マスのみを通ってゴールマス (入力で与えられる) に到達したいです。

そのための最小移動回数を求めてください。

制約

$1 \le R, C \le 50$
スタートマスからゴールマスへ到達できることが保証される

解法

まさに幅優先探索 (BFS) の練習問題ですね！

BFS については、次の記事たちで詳しく解説しています。いずれも僕の書いたものです。

qiita.com

algo-method.com

幅優先探索を踏まえた上で、この「迷路の最短路」を解くためには、上下左右のマスへの移動をプログラム上で効率よく実装する必要があります。次のように、4 方向への移動をあらかじめ定義する方法が主流です。

const vector<int> dx = {1, 0, -1, 0};
const vector<int> dy = {0, 1, 0, -1};

具体的な使い方については、コード例を参考にしてもらえたらと思います。

最後に計算量を評価します。一般に、頂点数 $N$ 、辺数 $M$ のグラフを BFS するときの計算量は $O(N + M)$ となります。今回は、

マス (グラフの頂点) の個数： $O(RC)$
隣接するマスの組 (グラフの頂点) の個数： $O(RC)$ (各マスにつき隣接するマスは 4 個以下であるため)

であることから、BFS するための計算量は $O(RC)$ となります。

コード

#include <bits/stdc++.h>
using namespace std;

// マス間の上下左右への移動を定義する
const vector<int> dx = {1, 0, -1, 0};
const vector<int> dy = {0, 1, 0, -1};

// マスを表す型。上から x 行目、左から y 列目のマスを {x, y}　で表すこととする
using pint = pair<int,int>;

int main() {
    // 入力
    int R, C, sx, sy, tx, ty;
    cin >> R >> C >> sx >> sy >> tx >> ty;
    --sx, --sy, --tx, --ty;  // 0-indexed にする
    vector<string> field(R);
    for (int i = 0; i < R; ++i) cin >> field[i];
    
    // 幅優先探索を実行するためのデータ構造
    // dist[x][y] はスタートマスからマス (x, y) までの最短路の長さ
    queue<pint> que;
    vector<vector<int>> dist(R, vector<int>(C, -1));
    
    // 初期条件
    que.push({sx, sy});
    dist[sx][sy] = 0;
    
    // 幅優先探索をスタート
    while (!que.empty()) {
        // 現在地はマス (x, y)
        auto [x, y] = que.front();
        que.pop();
        
        // 4 方向への移動を試す
        for (int dir = 0; dir < 4; ++dir) {
            int x2 = x + dx[dir];
            int y2 = y + dy[dir];
            
            // 新たなマスが場外の場合はダメ
            if (x2 < 0 || x2 >= R || y2 < 0 || y2 >= C) continue;
            
            // 新たなマスが壁の場合はダメ
            if (field[x2][y2] == '#') continue;
            
            // 新たなマスが訪問済みの場合はスキップ
            if (dist[x2][y2] != -1) continue;
            
            // 新たなマスを訪問する
            que.push({x2, y2});
            dist[x2][y2] = dist[x][y] + 1;
        }
    }
    cout << dist[tx][ty] << endl;
}

けんちょんの競プロ精進記録

競プロの精進記録や小ネタを書いていきます

AtCoder ABC 007 C - 幅優先探索 (試験管緑色)

問題概要

制約

解法

コード