2023-10-19

Cartesian Tree の実装〜 stack を用いた O(N) 時間構築

YosupoLibraryChecker Cartesian木データ構造 stack 入れ子構造非自明な線形時間テーマ解説記事

Cartesian Tree を実装しよう！　具体的には、Yosupo Library Checker の問題「Cartesian Tree」を通すことにする。

問題概要

長さ $N$ の数列 $A_{1}, A_{2}, \dots, A_{N}$ (互いに異なる) から誘導される Cartesian Tree を求めて出力せよ。

具体的には Cartesian Tree の各頂点について、その親頂点の番号を出力せよ (根については自分自身を親とする)。

ただし、数列中の最も小さい要素を根とすることにする。

制約

$1 \le N \le 10^{6}$
$0 \le A_{i} \le 10^{9}$

Cartesian Tree とは

数列から誘導される Cartesian Tree とは、下図のような二分木だ (wikipedia より)。まず、根は、数列全体の最小要素に対応していて、

根の左側頂点は「数列全体の最小要素より左側の区間」における最小の要素 (下図では、[9, 3, 7] の最小値である "3")
根の右側頂点は「数列全体の最小要素より右側の区間」における最小の要素 (下図では、[8, 12, 10, 20, 15, 18, 5] の最小値である "5")

に対応する。以降、再帰的に頂点数 $N$ の二分木を構成する。数列の index で見ると二分探索木になっていて、数列の要素値で見るとヒープになっているという、興味深い二分木だ。

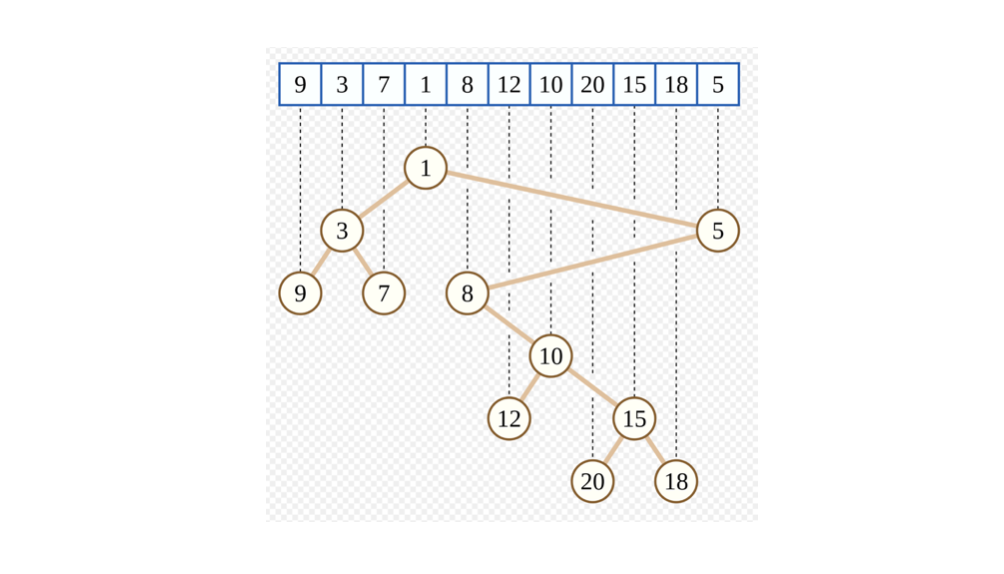
この Cartesian Tree は、数列を探索するときに最小値で左右に分割していくような分割統治法と相性がいい。

Cartesian Tree の構築

Cartesian Tree は、愚直にはセグ木や Sparse Table などを用いることで、計算量 $O(N \log N)$ で構築できそうだ。

しかし、実は stack を用いて $O(N)$ でできる。やり方は「ヒストグラム内部の極大長方形を求める」線形時間アルゴリズムにとてもよく似ている。

数列を前から順に見ていく。stack は常に次の状態を保持するようにする。

stack の先頭要素 $v_{1}$ は、数列の先頭から今まで見てきた要素の中で最小の要素である
stack の 2 番目の要素 $v_{2}$ は、数列の $v_{1}$ よりも後ろの要素から今まで見てきた要素の中で最小の要素である
stack の 3 番目の要素 $v_{3}$ は、数列の $v_{2}$ よりも後ろの要素から今まで見てきた要素の中で最小の要素である
...

つまり、stack の中身はつねに単調増加になっている。

たとえば、数列 [9, 3, 7, 1, 8, 12, 10, 20, 15, 18, 5] を例に取ると、次のように動作させる。

数列の要素	スタックの中身	備考
9	{9}
3	{3}	3 は 9 より小さいので 9 を pop したのち、3 を push する
7	{3, 7}	7 は 3 より大きいのでそのまま push する
1	{1}	7 も 3 も 1 より小さいのですべて pop したのち、1 を push する
8	{1, 8}	8 は 1 より大きいのでそのまま push する
12	{1, 8, 12}	12 は 8 より大きいのでそのまま push する
10	{1, 8, 10}	10 は 8 と 12 の間の数なので、12 まで pop して、8 の後ろに 10 を push する
20	{1, 8, 10, 20}	20 をそのまま push する
15	{1, 8, 10, 15}	20 を pop して、10 の後ろに 15 を push する
18	{1, 8, 10, 15, 18}	15 の後ろに 18 を push する
5	{1, 5}	18, 15, 10, 8 を pop して、1 の後ろに 5 を push する

決して難しくない、単純明快なアルゴリズムだ。そして実は、このアルゴリズムを回す過程で自然に Cartesian Tree が構築される。下図は、数列の最後の要素 5 を挿入する前後の Cartesian Tree を表している。

具体的には、次のようにすればよい。

stack の末尾の要素に対して、値を push するとき：
- $v$ の親を $s$ にする
- $s$ の右子を $v$ にする ( $s$ がすでに右子をもつ場合は入れ替える)
stack の末尾の要素に対して、値との比較によって pop するとき：
- その最後に pop した要素を $s$ とする
- $v$ の左子を $s$ にする
- $s$ の親を $v$ にする ( $s$ がすでに親をもつ場合は入れ替える)

stack に 5 を挿入するとき、stack の末尾から 18, 15, 10, 8 を順に pop して、1 の後ろに push する。最後に pop するのが 8 なので、8 が 5 の左子になり、1 の後ろに push するので、1 が 8 の親になっている。

以上の Cartesian Tree 構築アルゴリズムは次のコードのように実装できる。計算量は $O(N)$ である。

コード

#include <bits/stdc++.h>
using namespace std;
using pll = pair<long long, long long>;


// Cartesian Tree
template<class T> struct CartesianTree {
    int root;  // root
    vector<int> par, left, right;

    CartesianTree() {}
    CartesianTree(const vector<T>& v) :
    par(v.size(), -1), left(v.size(), -1), right(v.size(), -1) {
        vector<int> st(v.size(), 0);
        int top = 0;
        for (int i = 1; i < v.size(); ++i) {
            if (v[st[top]] > v[i]) {
                while (top >= 1 && v[st[top - 1]] > v[i]) --top;
                left[i] = st[top];
                par[left[i]] = i;
                if (top == 0) {
                    root = i;
                } else {
                    par[i] = st[top - 1];
                    right[par[i]] = i;
                }
                st[top] = i;
            } else {
                par[i] = st[top];
                right[par[i]] = i;
                st[++top] = i;
            }
        }
    }
};


void YosupoJudgeCartesianTree() {
    int N;
    cin >> N;
    vector<int> a(N);
    for (int i = 0; i < N; ++i) cin >> a[i];

    CartesianTree<int> ct(a);
    for (int i = 0; i < ct.par.size(); ++i) {
        cout << (ct.par[i] != -1 ? ct.par[i] : i) <<  " ";
    }
    cout << endl;
}

int main() {
    YosupoJudgeCartesianTree();
}