問題概要

$N$ 個の英小文字からなる文字列 $S_{1}, S_{2}, \dots, S_{N}$ が与えられる。

これら $N$ 個の文字列について、連続する部分文字列をすべて考える。重複を除かずに考えると $M = \displaystyle \sum_{i=1}^{N} \frac{|S_{i}|(|S_{i}|+1)}{2}$ 個ある。

これら $M$ 個の文字列を辞書順にソートしたい。 $Q$ 個の整数 $1 \le x_{1} \lt x_{2} \lt \dots \lt x_{Q} \le M$ が与えられるので、各 $q$ に対して、辞書順で $x_{q}$ 番目の文字列を求めよ。

具体的には、その文字列が $S_{K}$ の $L$ 文字目から $R$ 文字目までに一致するとき、3 つの整数組 $(K, L, R)$ を出力せよ。複数通りある場合はどれを出力してもよい。

制約

$1 \le N \le 10^{5}$
$\sum_{i=1}^{N}|S_{i}| \le 10^{5}$
$1 \le Q \le 2 \times 10^{5}$

考えたこと

文字列 $S_{1}, S_{2}, \dots, S_{N}$ を "$" で挟んで連結した文字列 $T$ の Suffix Tree を考える。ただし、各 suffix において、"$" 以降は無視するようにする。

たとえば、 $S =$ ("aabb", "abababc") のとき、 $T =$ "aabb$abababc" となり、 $T$ の Suffix Array は次のようになる。

0 番目：""
1 番目："$abababc"
2 番目："aabb$abababc"
3 番目："abababc"
4 番目："ababc"
5 番目："abb$abababc"
6 番目："abc"
7 番目："b$abababc"
8 番目："bababc"
9 番目："babc"
10 番目："bb$abababc"
11 番目："bc"
12 番目："c"

よって、 $T$ の Suffix Tree は下図のようになる。"$" 以降を無視する操作は、高さ配列 lcp の値を適切に変形しておくことで実現できる。

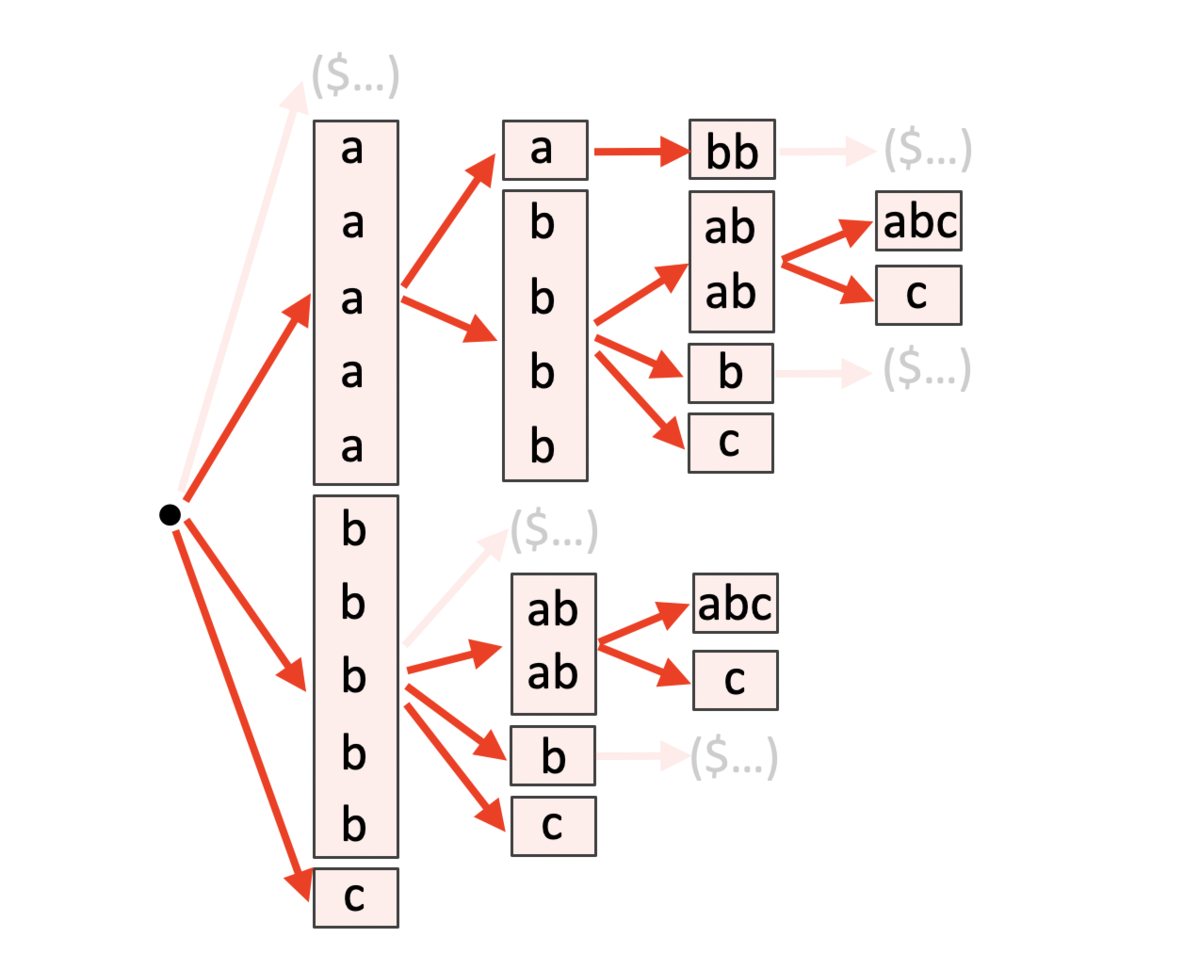
求める文字列の辞書順は、この木の各ノードを dfs することで得られる。上図の場合、次のようになる。

"a", "a", "a", "a", "a"
"aa"
"aab"
"aabb"
"ab", "ab", "ab", "ab"
"aba", "aba"
"abab", "abab"
"ababa"
"ababab"
"abababc"
"ababc"
"abb"
"abc"
"b", "b", "b", "b", "b"
"ba", "ba"
"bab", "bab"
"baba"
"babab"
"bababc"
"babc"
"bb"
"bc"
"c"

各ノードは、suffix array の左端 left、右端 right と、深さ depth の 3 つの値で管理することにした。

計算量を評価する。Suffix Array のノード数は、 $D = \sum_{i=1}^{N} |S_{i}|$ として $O(D)$ となる。下の実装では、区間 [left, right) を再帰的に分割していく部分で、高さ配列 lcp を乗せたセグメント木を用いているため、計算量は全体として $O(D \log D + Q)$ となる。

コード

#include <bits/stdc++.h>
using namespace std;
using pint = pair<int, int>;
using pll = pair<long long, long long>;
template<class T> inline bool chmax(T& a, T b) { if (a < b) { a = b; return 1; } return 0; }
template<class T> inline bool chmin(T& a, T b) { if (a > b) { a = b; return 1; } return 0; }

// Segment Tree
template<class Monoid> struct SegTree {
    using Func = function<Monoid(Monoid, Monoid)>;
    int N;
    Func F;
    Monoid IDENTITY;
    int SIZE_R;
    vector<Monoid> dat;

    /* initialization */
    SegTree() {}
    SegTree(int n, const Func f, const Monoid &identity)
    : N(n), F(f), IDENTITY(identity) {
        SIZE_R = 1;
        while (SIZE_R < n) SIZE_R *= 2;
        dat.assign(SIZE_R * 2, IDENTITY);
    }
    void init(int n, const Func f, const Monoid &identity) {  
        N = n;
        F = f;
        IDENTITY = identity;
        SIZE_R = 1;
        while (SIZE_R < n) SIZE_R *= 2;
        dat.assign(SIZE_R * 2, IDENTITY);
    }
    
    /* set, a is 0-indexed */
    /* build(): O(N) */
    void set(int a, const Monoid &v) { dat[a + SIZE_R] = v; }
    void build() {
        for (int k = SIZE_R - 1; k > 0; --k)
            dat[k] = F(dat[k*2], dat[k*2+1]);
    }
    
    /* update a, a is 0-indexed, O(log N) */
    void update(int a, const Monoid &v) {
        int k = a + SIZE_R;
        dat[k] = v;
        while (k >>= 1) dat[k] = F(dat[k*2], dat[k*2+1]);
    }
    
    /* get [a, b), a and b are 0-indexed, O(log N) */
    Monoid get(int a, int b) {
        Monoid vleft = IDENTITY, vright = IDENTITY;
        for (int left = a + SIZE_R, right = b + SIZE_R; left < right; 
        left >>= 1, right >>= 1) {
            if (left & 1) vleft = F(vleft, dat[left++]);
            if (right & 1) vright = F(dat[--right], vright);
        }
        return F(vleft, vright);
    }
    Monoid all_get() { return dat[1]; }
    Monoid operator [] (int a) { return dat[a + SIZE_R]; }
    
    /* get max r that f(get(l, r)) = True (0-indexed), O(log N) */
    /* f(IDENTITY) need to be True */
    int max_right(const function<bool(Monoid)> f, int l = 0) {
        if (l == N) return N;
        l += SIZE_R;
        Monoid sum = IDENTITY;
        do {
            while (l % 2 == 0) l >>= 1;
            if (!f(F(sum, dat[l]))) {
                while (l < SIZE_R) {
                    l = l * 2;
                    if (f(F(sum, dat[l]))) {
                        sum = F(sum, dat[l]);
                        ++l;
                    }
                }
                return l - SIZE_R;
            }
            sum = F(sum, dat[l]);
            ++l;
        } while ((l & -l) != l);  // stop if l = 2^e
        return N;
    }

    /* get min l that f(get(l, r)) = True (0-indexed), O(log N) */
    /* f(IDENTITY) need to be True */
    int min_left(const function<bool(Monoid)> f, int r = -1) {
        if (r == 0) return 0;
        if (r == -1) r = N;
        r += SIZE_R;
        Monoid sum = IDENTITY;
        do {
            --r;
            while (r > 1 && (r % 2)) r >>= 1;
            if (!f(F(dat[r], sum))) {
                while (r < SIZE_R) {
                    r = r * 2 + 1;
                    if (f(F(dat[r], sum))) {
                        sum = F(dat[r], sum);
                        --r;
                    }
                }
                return r + 1 - SIZE_R;
            }
            sum = F(dat[r], sum);
        } while ((r & -r) != r);
        return 0;
    }
    
    /* debug */
    void print() {
        for (int i = 0; i < N; ++i) {
            cout << (*this)[i];
            if (i != N-1) cout << ",";
        }
        cout << endl;
    }
};

// SA-IS (O(N))
template<class Str> struct SuffixArray {
    // data
    Str str;
    vector<int> sa;    // sa[i] : the starting index of the i-th smallest suffix (i = 0, 1, ..., n)
    vector<int> rank;  // rank[sa[i]] = i
    vector<int> lcp;   // lcp[i]: the lcp of sa[i] and sa[i+1] (i = 0, 1, ..., n-1)

    // getter
    int& operator [] (int i) {
        return sa[i];
    }
    vector<int> get_sa() { return sa; }
    vector<int> get_rank() { return rank; }
    vector<int> get_lcp() { return lcp; }

    // constructor
    SuffixArray() {}
    SuffixArray(const Str& str_) : str(str_) {
        build_sa();
    }
    void init(const Str& str_) {
        str = str_;
        build_sa();
    }
    void build_sa() {
        vector<int> s;
        for (int i = 0; i < (int)str.size(); ++i) {
            s.push_back(str[i] + 1);
        }
        s.push_back(0);
        sa = sa_is(s);
        calcLCP(s);
    }

    // SA-IS
    // upper: # of characters 
    vector<int> sa_is(vector<int> &s, int upper = 256) {
        int N = (int)s.size();
        if (N == 0) return {};
        else if (N == 1) return {0};
        else if (N == 2) {
            if (s[0] < s[1]) return {0, 1};
            else return {1, 0};
        }

        vector<int> isa(N);
        vector<bool> ls(N, false);
        for (int i = N - 2; i >= 0; --i) {
            ls[i] = (s[i] == s[i + 1]) ? ls[i + 1] : (s[i] < s[i + 1]);
        }
        vector<int> sum_l(upper + 1, 0), sum_s(upper + 1, 0);
        for (int i = 0; i < N; ++i) {
            if (!ls[i]) ++sum_s[s[i]];
            else ++sum_l[s[i] + 1];
        }
        for (int i = 0; i <= upper; ++i) {
            sum_s[i] += sum_l[i];
            if (i < upper) sum_l[i + 1] += sum_s[i];
        }

        auto induce = [&](const vector<int> &lms) -> void {
            fill(isa.begin(), isa.end(), -1);
            vector<int> buf(upper + 1);
            copy(sum_s.begin(), sum_s.end(), buf.begin());
            for (auto d: lms) {
                if (d == N) continue;
                isa[buf[s[d]]++] = d;
            }
            copy(sum_l.begin(), sum_l.end(), buf.begin());
            isa[buf[s[N - 1]]++] = N - 1;
            for (int i = 0; i < N; ++i) {
                int v = isa[i];
                if (v >= 1 && !ls[v - 1]) {
                    isa[buf[s[v - 1]]++] = v - 1;
                }
            }
            copy(sum_l.begin(), sum_l.end(), buf.begin());
            for (int i = N - 1; i >= 0; --i) {
                int v = isa[i];
                if (v >= 1 && ls[v - 1]) {
                    isa[--buf[s[v - 1] + 1]] = v - 1;
                }
            }
        };
            
        vector<int> lms, lms_map(N + 1, -1);
        int M = 0;
        for (int i = 1; i < N; ++i) {
            if (!ls[i - 1] && ls[i]) {
                lms_map[i] = M++;
            }
        }
        lms.reserve(M);
        for (int i = 1; i < N; ++i) {
            if (!ls[i - 1] && ls[i]) {
                lms.push_back(i);
            }
        }
        induce(lms);

        if (M) {
            vector<int> lms2;
            lms2.reserve(isa.size());
            for (auto v: isa) {
                if (lms_map[v] != -1) lms2.push_back(v);
            }
            int rec_upper = 0;
            vector<int> rec_s(M);
            rec_s[lms_map[lms2[0]]] = 0;
            for (int i = 1; i < M; ++i) {
                int l = lms2[i - 1], r = lms2[i];
                int nl = (lms_map[l] + 1 < M) ? lms[lms_map[l] + 1] : N;
                int nr = (lms_map[r] + 1 < M) ? lms[lms_map[r] + 1] : N;
                bool same = true;
                if (nl - l != nr - r) same = false;
                else {
                    while (l < nl) {
                        if (s[l] != s[r]) break;
                        ++l, ++r;
                    }
                    if (l == N || s[l] != s[r]) same = false;
                }
                if (!same) ++rec_upper;
                rec_s[lms_map[lms2[i]]] = rec_upper;
            }
            auto rec_sa = sa_is(rec_s, rec_upper);

            vector<int> sorted_lms(M);
            for (int i = 0; i < M; ++i) {
                sorted_lms[i] = lms[rec_sa[i]];
            }
            induce(sorted_lms);
        }
        return isa;
    }

    // find min id that str.substr(sa[id]) >= T
    int lower_bound(const Str& T) {
        int left = -1, right = sa.size();
        while (right - left > 1) {
            int mid = (left + right) / 2;
            if (str.compare(sa[mid], string::npos, T) < 0)
                left = mid;
            else
                right = mid;
        }
        return right;
    }

    // find min id that str.substr(sa[id], T.size()) > T
    int upper_bound(const Str& T) {
        int left = -1, right = sa.size();
        while (right - left > 1) {
            int mid = (left + right) / 2;
            if (str.compare(sa[mid], T.size(), T) <= 0)
                left = mid;
            else
                right = mid;
        }
        return right;
    }

    // search
    bool is_contain(const Str& T) {
        int lb = lower_bound(T);
        if (lb >= sa.size()) return false;
        return str.compare(sa[lb], T.size(), T) == 0;
    }

    // find lcp
    void calcLCP(const vector<int> &s) {
        int N = (int)s.size();
        rank.assign(N, 0), lcp.assign(N, 0);
        for (int i = 0; i < N; ++i) rank[sa[i]] = i;
        int h = 0;
        for (int i = 0; i < N - 1; ++i) {
            int pi = sa[rank[i] - 1];
            if (h > 0) --h;
            for (; pi + h < N && i + h < N; ++h) {
                if (s[pi + h] != s[i + h]) break;
            }
            lcp[rank[i] - 1] = h;
        }
    }

    // debug
    void dump() {
        cout << str << endl;
        for (int i = 0; i < sa.size(); ++i) {
            cout << i << ": " << sa[i] << ", " << str.substr(sa[i]) << endl;
        }
    }
};

int main() {
    // 入力
    int N, Q;
    cin >> N;
    vector<string> S(N);
    string T;  // S を '$' を挟みながら連結したもの
    vector<int> lp(N), rp(N);  // T における S[i] 部分の始点と終点
    for (int i = 0; i < N; ++i) {
        cin >> S[i];
        if (i) T += "$";
        lp[i] = T.size(), T += S[i], rp[i] = T.size();
    }
    cin >> Q;
    vector<long long> x(Q);
    for (int i = 0; i < Q; ++i) cin >> x[i];

    // Suffix Array の構築
    SuffixArray<string> suf(T);
    vector<int> sa = suf.get_sa();
    vector<int> rank = suf.get_rank();
    vector<int> lcp = suf.get_lcp();

    // $ の影響を除くための処理
    // rem_len[i] := sa[i] を表す文字列の先頭から $ までの残り文字数
    // sid[i] := sa[i] を表す文字列に対応する S の id
    // sstart[i] := sa[i] を表す文字列が S[sid] の何文字から開始か
    vector<int> rem_len(sa.size()), sid(sa.size()), sstart(sa.size());
    for (int j = 0; j < N; ++j) {
        for (int i = lp[j]; i < rp[j]; ++i) {
            rem_len[rank[i]] = rp[j] - i;
            sid[rank[i]] = j;
            sstart[rank[i]] = i - lp[j];
        }
    }
    for (int i = 0; i < lcp.size(); ++i) {
        chmin(lcp[i], rem_len[i]);
        chmin(lcp[i], rem_len[i+1]);
    }

    // lcp をセグ木に乗せる
    SegTree<pll> seg(lcp.size()
                    , [&](pll a, pll b) { return min(a, b); }
                    , pll(1LL<<29, 1LL<<29));
    for (int i = 0; i < lcp.size(); ++i) seg.set(i, pll(lcp[i], i));
    seg.build();

    // suffix tree 上を dfs
    // suffix tree の区間 [left, right) の深さ depth のところを探索
    long long num = 0;
    int query = 0;
    auto dfs = [&](auto self, int left, int right, int depth) -> void {
        // 終端条件
        if (right - left <= 0) return;

        // 区間 [left, right) の共通接尾辞を求める
        auto [nex_depth, mid] = seg.get(left, right-1);
        if (right - left == 1) {
            mid = left;
            nex_depth = rem_len[left];
        }
        long long width = right - left;
        long long add = width * (nex_depth - depth);

        // num 〜 num + add の範囲内にある x を処理していく
        while (query < Q && x[query] <= num + add) {
            long long len = depth + (x[query] - num + width - 1) / width;
            cout << sid[mid]+1 << " " << sstart[mid]+1 << " "
                 << sstart[mid]+len << endl;
            ++query;
        }
        num += add;

        if (right - left == 1 && nex_depth == depth) return;
        
        // 再帰的に処理
        self(self, left, mid+1, nex_depth);
        self(self, mid+1, right, nex_depth);
    };
    dfs(dfs, 0, sa.size(), 0);
}

Cartesian 木で高速化

Suffix Tree は、高さ配列 lcp の Cartesian 木でもある。Cartesian 木の構築は線形時間でできることから、全体の計算量を $O(D + Q)$ に高速化できる。

#include <bits/stdc++.h>
using namespace std;
using pll = pair<long long, long long>;
template<class T> inline bool chmin(T& a, T b) { if (a > b) { a = b; return 1; } return 0; }

// Cartesian Tree
template<class T> struct CartesianTree {
    int root;  // root
    vector<int> par, left, right;

    CartesianTree() {}
    CartesianTree(const vector<T>& v) : root(0)
    , par(v.size(), -1), left(v.size(), -1), right(v.size(), -1) {
        vector<int> st(v.size(), 0);
        int top = 0;
        for (int i = 1; i < v.size(); ++i) {
            if (v[st[top]] > v[i]) {
                while (top >= 1 && v[st[top - 1]] > v[i]) --top;
                par[left[i] = st[top]] = i;
                if (top == 0) root = i;
                else right[par[i] = st[top - 1]] = i;
                st[top] = i;
            } else {
                right[par[i] = st[top]] = i;
                st[++top] = i;
            }
        }
    }
};               

// SA-IS (O(N))
template<class Str> struct SuffixArray {
    // data
    Str str;
    vector<int> sa;    // sa[i] : the starting index of the i-th smallest suffix (i = 0, 1, ..., n)
    vector<int> rank;  // rank[sa[i]] = i
    vector<int> lcp;   // lcp[i]: the lcp of sa[i] and sa[i+1] (i = 0, 1, ..., n-1)

    // getter
    int& operator [] (int i) {
        return sa[i];
    }
    vector<int> get_sa() { return sa; }
    vector<int> get_rank() { return rank; }
    vector<int> get_lcp() { return lcp; }

    // constructor
    SuffixArray() {}
    SuffixArray(const Str& str_) : str(str_) {
        build_sa();
    }
    void init(const Str& str_) {
        str = str_;
        build_sa();
    }
    void build_sa() {
        vector<int> s;
        for (int i = 0; i < (int)str.size(); ++i) {
            s.push_back(str[i] + 1);
        }
        s.push_back(0);
        sa = sa_is(s);
        calcLCP(s);
    }

    // SA-IS
    // upper: # of characters 
    vector<int> sa_is(vector<int> &s, int upper = 256) {
        int N = (int)s.size();
        if (N == 0) return {};
        else if (N == 1) return {0};
        else if (N == 2) {
            if (s[0] < s[1]) return {0, 1};
            else return {1, 0};
        }

        vector<int> isa(N);
        vector<bool> ls(N, false);
        for (int i = N - 2; i >= 0; --i) {
            ls[i] = (s[i] == s[i + 1]) ? ls[i + 1] : (s[i] < s[i + 1]);
        }
        vector<int> sum_l(upper + 1, 0), sum_s(upper + 1, 0);
        for (int i = 0; i < N; ++i) {
            if (!ls[i]) ++sum_s[s[i]];
            else ++sum_l[s[i] + 1];
        }
        for (int i = 0; i <= upper; ++i) {
            sum_s[i] += sum_l[i];
            if (i < upper) sum_l[i + 1] += sum_s[i];
        }

        auto induce = [&](const vector<int> &lms) -> void {
            fill(isa.begin(), isa.end(), -1);
            vector<int> buf(upper + 1);
            copy(sum_s.begin(), sum_s.end(), buf.begin());
            for (auto d: lms) {
                if (d == N) continue;
                isa[buf[s[d]]++] = d;
            }
            copy(sum_l.begin(), sum_l.end(), buf.begin());
            isa[buf[s[N - 1]]++] = N - 1;
            for (int i = 0; i < N; ++i) {
                int v = isa[i];
                if (v >= 1 && !ls[v - 1]) {
                    isa[buf[s[v - 1]]++] = v - 1;
                }
            }
            copy(sum_l.begin(), sum_l.end(), buf.begin());
            for (int i = N - 1; i >= 0; --i) {
                int v = isa[i];
                if (v >= 1 && ls[v - 1]) {
                    isa[--buf[s[v - 1] + 1]] = v - 1;
                }
            }
        };
            
        vector<int> lms, lms_map(N + 1, -1);
        int M = 0;
        for (int i = 1; i < N; ++i) {
            if (!ls[i - 1] && ls[i]) {
                lms_map[i] = M++;
            }
        }
        lms.reserve(M);
        for (int i = 1; i < N; ++i) {
            if (!ls[i - 1] && ls[i]) {
                lms.push_back(i);
            }
        }
        induce(lms);

        if (M) {
            vector<int> lms2;
            lms2.reserve(isa.size());
            for (auto v: isa) {
                if (lms_map[v] != -1) lms2.push_back(v);
            }
            int rec_upper = 0;
            vector<int> rec_s(M);
            rec_s[lms_map[lms2[0]]] = 0;
            for (int i = 1; i < M; ++i) {
                int l = lms2[i - 1], r = lms2[i];
                int nl = (lms_map[l] + 1 < M) ? lms[lms_map[l] + 1] : N;
                int nr = (lms_map[r] + 1 < M) ? lms[lms_map[r] + 1] : N;
                bool same = true;
                if (nl - l != nr - r) same = false;
                else {
                    while (l < nl) {
                        if (s[l] != s[r]) break;
                        ++l, ++r;
                    }
                    if (l == N || s[l] != s[r]) same = false;
                }
                if (!same) ++rec_upper;
                rec_s[lms_map[lms2[i]]] = rec_upper;
            }
            auto rec_sa = sa_is(rec_s, rec_upper);

            vector<int> sorted_lms(M);
            for (int i = 0; i < M; ++i) {
                sorted_lms[i] = lms[rec_sa[i]];
            }
            induce(sorted_lms);
        }
        return isa;
    }

    // find min id that str.substr(sa[id]) >= T
    int lower_bound(const Str& T) {
        int left = -1, right = sa.size();
        while (right - left > 1) {
            int mid = (left + right) / 2;
            if (str.compare(sa[mid], string::npos, T) < 0)
                left = mid;
            else
                right = mid;
        }
        return right;
    }

    // find min id that str.substr(sa[id], T.size()) > T
    int upper_bound(const Str& T) {
        int left = -1, right = sa.size();
        while (right - left > 1) {
            int mid = (left + right) / 2;
            if (str.compare(sa[mid], T.size(), T) <= 0)
                left = mid;
            else
                right = mid;
        }
        return right;
    }

    // search
    bool is_contain(const Str& T) {
        int lb = lower_bound(T);
        if (lb >= sa.size()) return false;
        return str.compare(sa[lb], T.size(), T) == 0;
    }

    // find lcp
    void calcLCP(const vector<int> &s) {
        int N = (int)s.size();
        rank.assign(N, 0), lcp.assign(N - 1, 0);
        for (int i = 0; i < N; ++i) rank[sa[i]] = i;
        int h = 0;
        for (int i = 0; i < N - 1; ++i) {
            int pi = sa[rank[i] - 1];
            if (h > 0) --h;
            for (; pi + h < N && i + h < N; ++h) {
                if (s[pi + h] != s[i + h]) break;
            }
            lcp[rank[i] - 1] = h;
        }
    }

    // debug
    void dump() {
        cout << str << endl;
        for (int i = 0; i < sa.size(); ++i) {
            cout << i << ": " << sa[i] << ", " << str.substr(sa[i]) << endl;
        }
    }
};

void ABC280Ex() {
    // 入力
    int N, Q;
    cin >> N;
    vector<string> S(N);
    string T;  // S を '$' を挟みながら連結したもの
    vector<int> lp(N), rp(N);  // T における S[i] 部分の始点と終点
    for (int i = 0; i < N; ++i) {
        cin >> S[i];
        if (i) T += "$";
        lp[i] = T.size(), T += S[i], rp[i] = T.size();
    }
    cin >> Q;
    vector<long long> x(Q);
    for (int i = 0; i < Q; ++i) cin >> x[i];

    // Suffix Array の構築
    SuffixArray<string> suf(T);
    vector<int> sa = suf.get_sa();
    vector<int> rank = suf.get_rank();
    vector<int> lcp = suf.get_lcp();

    // $ の影響を除くための処理
    // rem_len[i] := sa[i] を表す文字列の先頭から $ までの残り文字数
    // sid[i] := sa[i] を表す文字列に対応する S の id
    // sstart[i] := sa[i] を表す文字列が S[sid] の何文字から開始か
    vector<int> rem_len(sa.size()), sid(sa.size()), sstart(sa.size());
    for (int j = 0; j < N; ++j) {
        for (int i = lp[j]; i < rp[j]; ++i) {
            rem_len[rank[i]] = rp[j] - i;
            sid[rank[i]] = j;
            sstart[rank[i]] = i - lp[j];
        }
    }
    for (int i = 0; i < lcp.size(); ++i) {
        chmin(lcp[i], rem_len[i]);
        chmin(lcp[i], rem_len[i+1]);
    }

    // suffix tree: lcp の Cartesian 木
    CartesianTree<int> ct(lcp);

    // suffix tree 上を dfs
    // suffix tree の区間 [left, right), 最小値 mid の深さ depth のところを探索
    long long num = 0;
    int query = 0;
    auto dfs = [&](auto self, int left, int right, int mid, int depth) -> void {
        // 終端条件
        if (right - left <= 0) return;

        // mid の処理
        if (right - left == 1) mid = left;

        // num 〜 num + add の範囲内にある x を処理していく
        long long width = right - left;
        long long nex_depth = (right - left > 1 ? lcp[mid] : rem_len[left]);
        long long add = width * (nex_depth - depth);
        while (query < Q && x[query] <= num + add) {
            long long len = depth + (x[query] - num + width - 1) / width;
            cout << sid[mid]+1 << " " << sstart[mid]+1 << " "
                 << sstart[mid]+len << endl;
            ++query;
        }
        num += add;
        
        // 再帰的に処理
        if (right - left > 1) {
            self(self, left, mid+1, ct.left[mid], nex_depth);
            self(self, mid+1, right, ct.right[mid], nex_depth);
        }
    };
    dfs(dfs, 0, sa.size(), ct.root, 0);
}

int main() {
    //YosupoJudge();
    ABC280Ex();
}