AtCoder ABC 143 D - Triangles (茶色, 400 点)

教育的ないい問題！！！！！

問題へのリンク

問題概要

本の棒があって、それぞれ の長さをもっている。

このうちの 3 本を選ぶ方法であって、その 3 本で三角形が作れるものは何通あるか？

制約

• 
• 

解法の overview

ものすごく色んな解法が考えられる問題だと思う。まずナイーブには 通りの選び方を全探索する方法が考えられる。しかし かかって間に合わない
(上手く枝刈りすると間に合ってしまったらしいが...)

そこで、こういうときによく考えるのが

---

3 つのうち、2 つを固定して考える

---

というあたり。とりあえず三角形の三辺を短い順に () として、

• を固定
• を固定

といったあたりが思いつく。どちらでやっても解ける。ここでは を固定してやってみる。

解法 1： 二分探索

のうちの を固定すると、残りの辺 の満たすべき条件は

• 

となる。下図のような感じ。 のとき、 なので、 のとりうる範囲は、下図のように

• より右側
• 未満の領域

ということになる。

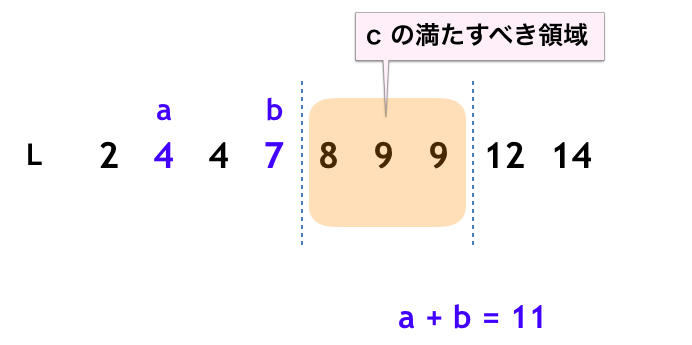
ここで、 のうち「最初に 以上になってしまうインデックス」は二分探索で求めることができる。lower_bound() とか使えば OK。

まとめると

• を全探索
• の中で最初に 以上になってしまうインデックスを求める
• の動ける範囲がそれによって求まるので、合計していく

という風に解ける。 の固定方法が だけあって、それに応じて の動ける範囲を求めるのは二分探索で でできるので、全体の計算量は となる。

#include <iostream>
#include <vector>
#include <algorithm>
using namespace std;

int main() {
    int N; cin >> N;
    vector<long long> L(N);
    for (int i = 0; i < N; ++i) cin >> L[i];
    sort(L.begin(), L.end()); // L をソートしておく (二分探索に必要)

    long long res = 0;
    
    // a と b を固定
    for (int i = 0; i < N; ++i) {
        for (int j = i+1; j < N; ++j) {
            // c の動ける範囲の右端を求める
            int k = lower_bound(L.begin(), L.end(), L[i] + L[j]) - L.begin();

            // c の動ける範囲は、[j+1, k)
            res += max(k - (j+1), 0);
        }
    }
    cout << res << endl;
}

解法 2： しゃくとり法

解法 1 では を固定した。そこでは

• を固定して
• の動く範囲の右端 ( の中で最初に 以上になってしまう場所) を求める

という風にしていた。ここでもっと突き詰めて

• を固定する
• を動かしていくと、 の右端が右へと単調にズレていく

ということがわかるので、しゃくとり法を使うことができる。

つまり、初期設定として、b を a の場所に、c を b の場所に設定しておいて、

---

• b を右に動かす
• c >= a + b になるまで c を右に動かす

---

をくりかえせば OK。計算量は各 に対して でできるので、全体として となる。

#include <iostream>
#include <vector>
#include <algorithm>
using namespace std;

int main() {
    int N; cin >> N;
    vector<long long> L(N);
    for (int i = 0; i < N; ++i) cin >> L[i];
    sort(L.begin(), L.end()); // L をソートしておく

    long long res = 0;
    
    // a を固定して、(b, c) をしゃくとり法
    for (int i = 0; i < N; ++i) {
        int k = i;
        for (int j = i+1; j < N; ++j) {
            while (k < N && L[k] < L[i]+L[j]) ++k;
            res += k - (j+1);
        }   
    }
    cout << res << endl;
}

解法 3： L が小さいことを活かして累積和

今回の問題は の制約がとても小さいことがわかる。こういうときに、たとえば

• 

とかに対して

• 

とかにするのをよくやる。C[ i ] は、L の中に i が何個あるのかを表す。これのメリットは、

---

• L の中で x 以上 y 未満の値が何個あるのかが、累積和を使うと簡単にわかる。

• 具体的には C の累積和を S とすると、S[ y ] - S[ x ] で求められる

---

というもの。そして解法 1, 2 と違って、 を仮定せずに求めて、最後に 3! = 6 で割ることにする。

一般に三角形の三辺 に対して三角形になるための必要十分条件は、

• 

と表せる。ここでは を仮定していないことに注意。これを利用して

---

• を固定する
• そうすると の満たすべき条件は と簡単に表せるので、これを満たす の個数は、累積和を使って S[ ] - S[ abs() + ] と求められる！！！
  • ただし、この の範囲に や も含まれていたらその分を減らす

---

という風にすれば OK。計算量は、累積和計算に 、その後の処理に となる。

#include <iostream>
#include <vector>
#include <cmath>
#include <algorithm>
using namespace std;

const int MAX = 2100;

int main() {
    long long res = 0;
    int N; cin >> N;
    vector<long long> L(N);
    for (int i = 0; i < N; ++i) cin >> L[i];

    // C, S
    vector<long long> C(MAX, 0), S(MAX+1, 0);
    for (int i = 0; i < N; ++i) C[L[i]]++;
    for (int x = 0; x < MAX; ++x) S[x+1] = S[x] + C[x]; // 累積和
    
    // a と b を固定
    for (int i = 0; i < N; ++i) {
        for (int j = 0; j < N; ++j) {
            if (i == j) continue; // 同じものは選ばない
            
            // c の満たすべき値の区間を [left, right) で表す
            int left = abs(L[i] - L[j]) + 1;
            int right = L[i] + L[j];

            // 累積和で個数を求める
            int count = S[right] - S[left];
            if (left <= L[i] && L[i] < right) --count;
            if (left <= L[j] && L[j] < right) --count;

            res += max(count, 0);
        }
    }
    cout << res/6 << endl;
}