銅色 diff 問題が自力で解けて嬉しい。(修正：赤色になった)

問題概要

原点を中心とする半径 1 の円周上に $N$ 個の点 $P_{1}, \dots, P_{N}$ がある (偏角が入力として与えられる)。

これらの点からランダムに 3 点選んでできる三角形の内心の座標の期待値を求めよ。 $10^{-9}$ の精度で正解とする。

制約

$3 \le N \le 3000$

解法 1 (僕の解法)

${}_{N}{\rm C}_{3}$ 通りの三角形をすべて調べるのでは間に合わない。そこで、2 点を固定して、残りの 1 点を自由に選んだときの総和を高速に求められればよさそうだと思った。それができそうな構造を探すことにする。

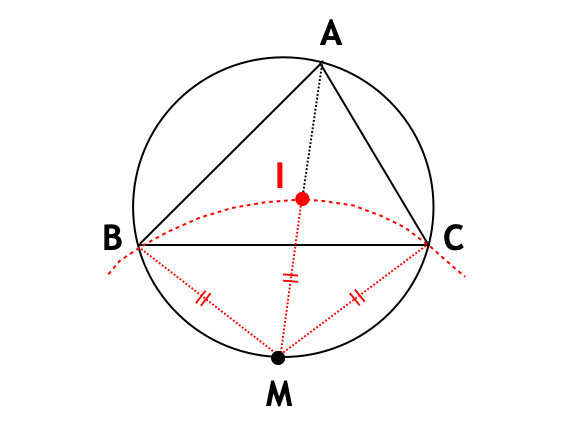
下図のように、辺 BC を固定したとき、内心 I は次の性質を満たす。ここで、

MB = MC = MI

が成り立つことは簡単な角度計算によってわかる (結構有名事実)。また下では、点 A, B, C の偏角を $L_{A}, L_{B}, L_{C}$ と表記している (三角形の内角ではない)。

三角形 ABC の内心 I は

弦 BC の中点を M としたとき
M を中心とする半径 MB (= MC) の円周上にあって、
その偏角は $90 + \frac{L_{B}+L_{C}}{4} + \frac{L_{A}}{2}$ 度となる

累積和解法へ

この性質を活用すれば、次の値が計算できればよいことがわかる。

$\alpha = 90 + \frac{L_{B}+L_{C}}{4}$

として、頂点 A の偏角を $t_{1}, \dots, t_{M}$ としたとき

$\cos (\frac{t_{1}}{2} + \alpha) + \dots + \cos (\frac{t_{M}}{2} + \alpha)$
$\sin (\frac{t_{1}}{2} + \alpha) + \dots + \sin (\frac{t_{M}}{2} + \alpha)$

の値が計算できればよい。角度 $\alpha$ がなければ「累積和」で管理できそう。でも角度 $\frac{t_{1}}{2}, \dots, \frac{t_{M}}{2}$ に $\alpha$ を足すのは単に

$\cos (\frac{t_{1}}{2}) + \dots + \cos (\frac{t_{M}}{2})$
$\sin (\frac{t_{1}}{2}) + \dots + \sin (\frac{t_{M}}{2})$

の値を $\alpha$ だけ回転させるだけなので問題ない。よって累積和を用いることで全体として $O(N^{2})$ の解法が得られた。

コード

#include <bits/stdc++.h>
using namespace std;

int main() {
    const double PI = acos(-1.0);
    long long N, L;
    cin >> N >> L;
    vector<double> T(N), csum(N+1, 0.0), ssum(N+1, 0.0);
    for (int i = 0; i < N; ++i) {
        cin >> T[i];
        T[i] *= PI * 2 / L;
        csum[i+1] = csum[i] + cos(T[i]/2);
        ssum[i+1] = ssum[i] + sin(T[i]/2);
    }

    double x = 0.0, y = 0.0;
    for (int i = 0; i < N; ++i) {
        for (int j = i+1; j < N; ++j) {
            double alpha = PI/2 + (T[i]+T[j])/4;
            double c = cos(alpha), s = sin(alpha);
            double bx = cos((T[i]+T[j])/2), by = sin((T[i]+T[j])/2);
            double R = sin((T[j]-T[i])/4) * 2.0; 
            double dx = c * (csum[N]-csum[j+1]) - s * (ssum[N]-ssum[j+1]);
            double dy = s * (csum[N]-csum[j+1]) + c * (ssum[N]-ssum[j+1]);
            x += bx * (N-j-1) + R * dx, y += by * (N-j-1) + R * dy;
        }
    }
    long long num = N * (N-1) * (N-2) / 6;
    x /= num, y /= num;
    cout << fixed << setprecision(10) << x << " " << y << endl;
}