早稲田大学プログラミングコンテスト WUPC 2019 F - RPG

フロー大好き！！！！！！！！

問題へのリンク

問題概要

頂点 辺の DAG が与えられる。頂点 からスタートして頂点 へと向かいたい。すべての頂点 に対し、 から へと向かうパスと、 から へと向かうパスが存在することが保証されている。

頂点のうちいくつかは「そこに行くと疲労する」という状態になっている。疲労した状態で、再び「疲労」頂点に行くとゲームオーバーである。

今、疲労頂点以外の頂点 にはコスト を払って「休憩所」を置くことができる。そうすると休憩所を通るときは「疲労」を「回復」することができる。

から へたどり着く任意の経路について、途中でゲームオーバーせずにクリアできるようにするのに必要な休憩所設置の最小コストを求めよ。不可能な場合は -1 を出力せよ。

制約

• 
• 

考えたこと

もし「経路を最適化して、休憩所設置コストを最小にせよ」という問題だったら、ただの最短路問題 (各ノードを「疲労」「元気」に分けてやる拡張 0-1 BFS) だった。

今回は「任意の経路について、途中でゲームオーバーせずに」ということで難しそうな設定に思える。しかしながら、任意の頂点 に対して、 から へ行けるし、 から にも行けるという制約があることから、 から へと至る経路に関係ないところでゲームオーバーしてしまう可能性を考えなくて良い。結局

• 「疲労」のまま次の「疲労」に至る可能性のあるパスのすべてについて、その可能性をつぶす

という問題だと思うことができる。つまり任意の疲労ノードのペア (DAG なのでどちらが始点かが一意に決まる、ここでは -> とする) について、 と とを結ぶパスを分断すればよい。これはカットに対応しそうである。

まず、疲労ノードを「始点用」と「終点用」とに分割する。そうしてスーパーノード s, t を用意して

• s から各疲労始点ノードに INF の辺を張る
• 各疲労終点ノードから t へ INF の辺を張る

という感じにする。こうしておいて普通にグラフを作ってあげて、通常ノードについては「頂点に容量がある」というタイプの最小カットにしたいのだが、頂点に容量があるという状況は、頂点を分割することで上手く表現できる。

結局グラフ全体について頂点を分割する感じになる。でも、

• 疲労ノードについての頂点分割のお気持ち (その間でカット作る)
• それ以外のノードについての頂点分割のお気持ち (あくまで頂点の容量を表現するためのもの)

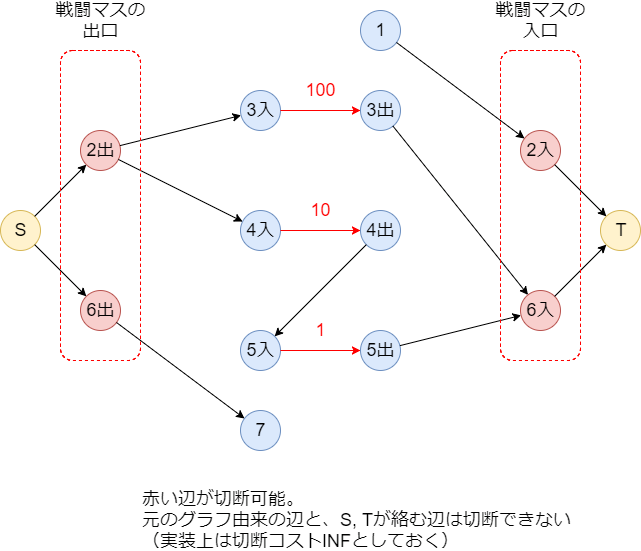
が違っていて、それにともなって辺の貼り方も違うのでちょっとややこしい。以下の図はアルメリアさんの記事からの引用で、

• 疲労ノードについては、そのノードから出る辺については「始点」ノードから辺を引っ張っていて、そのノードに入る辺については「終点」ノードへと辺を張っている
• それ以外のノードについては、そのノードから出る辺については「終点」ノードから辺を引っ張っていて、そのノードに入る辺については「始点」ノードへと辺を張っている

という感じになっている。

#include <iostream>
#include <vector>
#include <queue>
using namespace std;

// edge class (for network-flow)
template<class FLOWTYPE> struct Edge {
    int rev, from, to;
    FLOWTYPE cap, icap;
    Edge(int r, int f, int t, FLOWTYPE c) : rev(r), from(f), to(t), cap(c), icap(c) {}
    friend ostream& operator << (ostream& s, const Edge& E) {
        if (E.cap > 0) return s << E.from << "->" << E.to << '(' << E.cap << ')';
        else return s;
    }
};

// graph class (for network-flow)
template<class FLOWTYPE> struct Graph {
    vector<vector<Edge<FLOWTYPE> > > list;

    Graph(int n = 0) : list(n) { }
    void init(int n = 0) { list.clear(); list.resize(n); }
    void reset() { for (int i = 0; i < (int)list.size(); ++i) for (int j = 0; j < list[i].size(); ++j) list[i][j].cap = list[i][j].icap; }
    inline vector<Edge<FLOWTYPE> >& operator [] (int i) { return list[i]; }
    inline const size_t size() const { return list.size(); }

    inline Edge<FLOWTYPE> &redge(Edge<FLOWTYPE> e) {
        if (e.from != e.to) return list[e.to][e.rev];
        else return list[e.to][e.rev + 1];
    }

    void addedge(int from, int to, FLOWTYPE cap) {
        list[from].push_back(Edge<FLOWTYPE>((int)list[to].size(), from, to, cap));
        list[to].push_back(Edge<FLOWTYPE>((int)list[from].size() - 1, to, from, 0));
    }

    void add_undirected_edge(int from, int to, FLOWTYPE cap) {
        list[from].push_back(Edge<FLOWTYPE>((int)list[to].size(), from, to, cap));
        list[to].push_back(Edge<FLOWTYPE>((int)list[from].size() - 1, to, from, cap));
    }

    
    // debug
    friend ostream& operator << (ostream& s, const Graph& G) {
    s << endl; for (int i = 0; i < G.size(); ++i) { s << i << " : " << G.list[i] << endl; }return s;
    }
    
};

template<class FLOWTYPE> struct Dinic {
    const FLOWTYPE INF = 1LL << 60; // to be set
    vector<int> level, iter;

    Dinic() { }
    void dibfs(Graph<FLOWTYPE> &G, int s) {
        level.assign((int)G.size(), -1);
        level[s] = 0;
        queue<int> que;
        que.push(s);
        while (!que.empty()) {
            int v = que.front();
            que.pop();
            for (int i = 0; i < G[v].size(); ++i) {
                Edge<FLOWTYPE> &e = G[v][i];
                if (level[e.to] < 0 && e.cap > 0) {
                    level[e.to] = level[v] + 1;
                    que.push(e.to);
                }
            }
        }
    }

    FLOWTYPE didfs(Graph<FLOWTYPE> &G, int v, int t, FLOWTYPE f) {
        if (v == t) return f;
        for (int &i = iter[v]; i < G[v].size(); ++i) {
            Edge<FLOWTYPE> &e = G[v][i], &re = G.redge(e);
            if (level[v] < level[e.to] && e.cap > 0) {
                FLOWTYPE d = didfs(G, e.to, t, min(f, e.cap));
                if (d > 0) {
                    e.cap -= d;
                    re.cap += d;
                    return d;
                }
            }
        }
        return 0;
    }

    FLOWTYPE solve(Graph<FLOWTYPE> &G, int s, int t) {
        level.assign((int)G.size(), -1); iter.assign((int)G.size(), 0);
        FLOWTYPE res = 0;
        while (true) {
            dibfs(G, s);
            if (level[t] < 0) return res;
            for (int i = 0; i < (int)iter.size(); ++i) iter[i] = 0;
            FLOWTYPE flow = 0;
            while ((flow = didfs(G, s, t, INF)) > 0) {
                res += flow;
            }
        }
    }
};

int main() {
    int N, M; cin >> N >> M;
    vector<long long> c(N, -2);
    for (int i = 1; i < N - 1; ++i) cin >> c[i];
    vector<int> a(M), b(M);
    for (int i = 0; i < M; ++i) cin >> a[i] >> b[i], --a[i], --b[i];

    const long long INF = 1LL << 50;
    Graph<long long> G(N * 2 + 2);
    int s = N * 2, t = s + 1;

    // 頂点の分裂
    for (int v = 0; v < N; ++v) {
        if (c[v] > 0) {
            G.addedge(v, v + N, c[v]);
        }
    }

    // スーパーノード
    for (int v = 0; v < N; ++v) {
        if (c[v] == -1) {
            G.addedge(s, v, INF);
            G.addedge(v + N, t, INF);
        }
    }

    // グラフの形そのものを作る
    for (int i = 0; i < M; ++i) {
        int from = a[i] + N, to = b[i];
        if (c[a[i]] == -1) from = a[i];
        if (c[b[i]] == -1) to = b[i] + N;
        G.addedge(from, to, INF);
    }

    Dinic<long long> din;
    long long res = din.solve(G, s, t);
    cout << (res < INF ? res : -1) << endl;
}