めちゃいっぱい解法あってすごい！！！！！！！MST への理解が問われる。
いずれ復習をやり切ってちゃんとしたいが取り急ぎ、分割統治法 Kruskal と、想定解法のみ。

問題概要

$N$ 頂点からなるパスグラフと整数 $D$ が与えられる。各頂点には重み $A_v$ が与えられる。

ここで同じ頂点集合をもち各辺の重みが次のように定義される完全グラフを考える:

$(i, j)$ の重みは、 $D|i - j| + A_i + A_j$

この完全グラフの MST の重みを求めよ。

制約

$1 \le N \le 2 × 10^{5}$

こぼれ話

この問題は元のグラフがパスグラフバージョンだが、元のグラフがツリーバージョンが CODE FESTIVAL 2017 Finals J - Tree MST に出題されている！

そしてなんと、元のグラフが一般のグラフに対しても高速・省実装なグラフ上ボロノイ図解法がある！！！とこはるさんの記事に詳細がある。

また、この問題は元々、元のグラフがグリッドだったらしい。その場合でもグラフ上ボロノイ図解法が使える。

とにかく色んな解法があるみたいなので、徹底的に復習を試みる。

その前に最小全域木の性質

最小全域木について考察するときに、重要な性質を 2 つ！！！
下図の赤線が、最小全域木だとする。

最小全域木の性質 1: サイクルに関する最適性

下図のように、最小全域木に含まれない辺を 1 つ選ぶと、サイクルができる。下図では青線で示した辺を選ぶことで、太線で示したサイクルが形成される。

このとき、このサイクルの中で青線の辺は重みが最大である。

理由は明確で、もし重みが最小じゃなかったら、その最小の辺と青線とを入れ替えることで、重みが最小のはずの全域木の重みを減少させることができてしまう！！！

そして実はもっとすごいことに逆も言える。つまり、全域木が与えられたときに、任意のこのようなサイクルに対して新たに付け加えられる辺の重みが最小であるならば、与えられた全域木は最小全域木になっている！！！

この証明は、上記の性質を満たす全域木 $S$ が与えられたときに、最小全域木 $T$ をなにか 1 つとって来て、 $S$ の重みを変えずに上手く辺を入れ替えて $T$ に変形できることから示せる。

この最適性条件は、まさに Kruskal 法の正当性の証明にもなっている。

この辺りの話は、実はマトロイドに一般化できる。マトロイドの交換公理を学ぶと、上記のことはとても自然な概念に感じられる。

最小全域木の性質 2: カットに関する最適性

最小全域木に含まれる辺を 1 つ選ぶと、下図のように全域木は 2 つの部分に分かれ、その間にカットが芽生える。

このとき、このカットの中で太赤線の辺の重みは最小である。

理由はサイクルのときと一緒で、もし最小じゃなかったら最小の辺と入れ替えることで、全域木の重みを減少させることができてしまう。

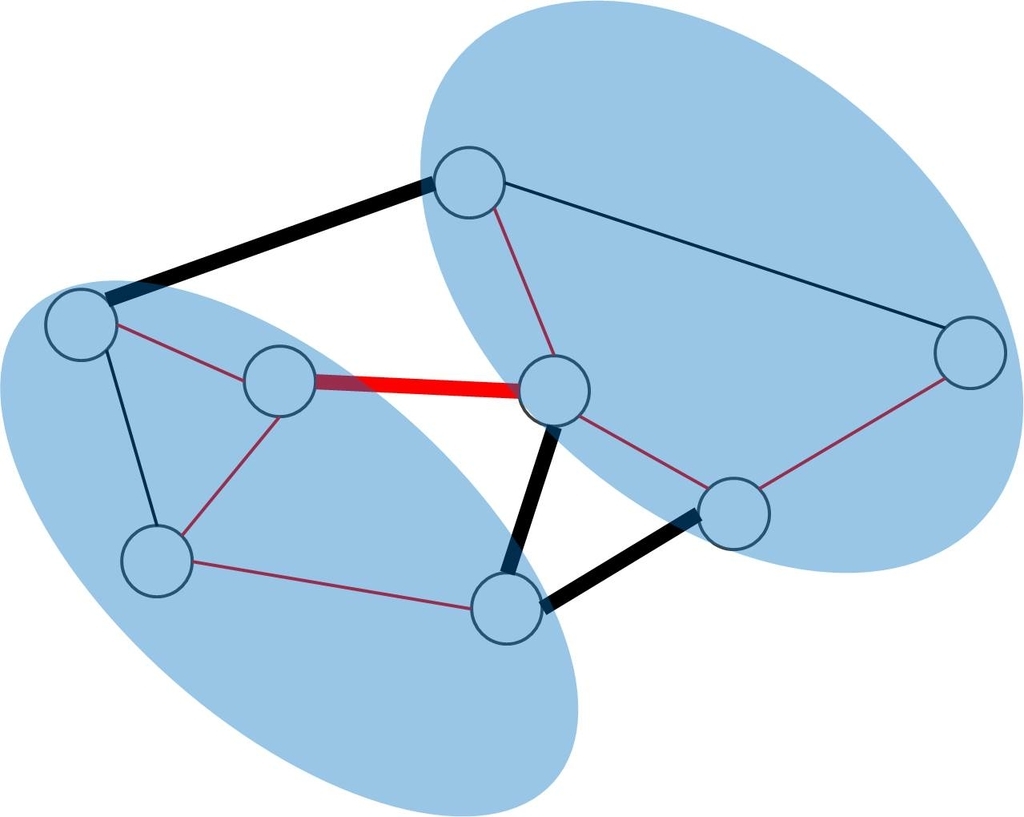
そしてサイクルのときと同様に逆も言えます。この事実は、Prim 法や Borůvka 法を支えるものになっています。

解法 1: Kruskal 法 with 分割統治法

あの「Tree MST」も殴れる解法。

下図のようにパスグラフを半分ずつに分けます。この 2 領域間を結ぶ辺のうち、最終的な最小全域木に使われる辺の候補としてあり得ないものを除外することを考えます。

この操作を再帰的に行って、結果として候補辺数は $O(N^{2})$ から $O(N\log{N})$ まで減少するので、最後にまとめて Kruskal 法をします。

さて、下図のように、まず赤側の頂点を 1 つ fix してあげて、青側の各頂点への辺を考えて、その中で重みが最小のものを考えます (下図ではそのような辺を赤く塗りました)。少し考えればわかることとして、最初に fix する赤側の頂点としてどれを選んでも、それに対して重み最小となる青側の頂点は 1 つに決まります (タイはあり得る)。具体的には青側の頂点 $v$ のうち、 $A_v + D × v$ が最小になるものです。

同様にして青側の各頂点に対しても、赤側の頂点が 1 つ存在して、その頂点への辺の重みが最小になっています。

そして驚くべきこととして、

各赤頂点からの、青側 min 頂点への辺
各青頂点からの、赤側 min 頂点への辺

以外は除去してしまってもよいことがわかります。ここで上述のサイクル最適性が使えます。具体的には下図のように

両端点ともに赤側 min でも青側 min でもない辺 (青く示した辺)

があると、下図のようにそれを含んだ長さ 4 のサイクルが作れます。ここで青辺はこのサイクルの中で重みが最大になってしまっています。よってそれを使うことなく最小全域木を構成することができます。

あとは、これを赤側、青側内部でも再帰的に行っていくことで、結局最後は $O(N\log{N})$ 個の辺だけが残ります。その中で改めて Kruskal 法を行えば良いです。計算量は $O(N(\log{n})^{2})$ になります。

なおこの解法で Tree MST を殴るときは、「ツリーの重心分解」による分割統治法を行えばよいです。

#include <iostream>
#include <vector>
#include <algorithm>
using namespace std;
template<class T> inline bool chmax(T& a, T b) { if (a < b) { a = b; return 1; } return 0; }
template<class T> inline bool chmin(T& a, T b) { if (a > b) { a = b; return 1; } return 0; }

struct UnionFind {
    vector<int> par;
    
    UnionFind(int n) : par(n, -1) { }
    void init(int n) { par.assign(n, -1); }
    
    int root(int x) {
        if (par[x] < 0) return x;
        else return par[x] = root(par[x]);
    }
    
    bool issame(int x, int y) {
        return root(x) == root(y);
    }
    
    bool merge(int x, int y) {
        x = root(x); y = root(y);
        if (x == y) return false;
        if (par[x] > par[y]) swap(x, y); // merge technique
        par[x] += par[y];
        par[y] = x;
        return true;
    }
    
    int size(int x) {
        return -par[root(x)];
    }
};

using pint = pair<int,int>;
using Edge = pair<long long,pint>;

// 入力
int N;
long long D;
vector<long long> A;

// 分割統治法
vector<Edge> edges;
void rec(int left, int right) {
    if (right - left <= 1) return;
    int mid = (left + right) / 2;
    
    long long leftmin = 1LL<<60;
    int leftminp = -1;
    for (int i = left; i < mid; ++i) if (chmin(leftmin, A[i]-D*i)) leftminp = i;
    long long rightmin = 1LL<<60;
    int rightminp = -1;
    for (int i = mid; i < right; ++i) if (chmin(rightmin, A[i]+D*i)) rightminp = i;
    
    for (int i = left; i < mid; ++i)
        edges.push_back(Edge(A[rightminp] + A[i] + D * (rightminp - i), pint(i, rightminp)));
    for (int i = mid; i < right; ++i)
        edges.push_back(Edge(A[leftminp] + A[i] + D * (i - leftminp), pint(leftminp, i)));
    
    rec(left, mid);
    rec(mid, right);
}

int main() {
    cin >> N >> D;
    A.resize(N);
    for (int i = 0; i < N; ++i) cin >> A[i];
    
    // 分割統治法
    edges.clear();
    rec(0, N);
    
    // Kruskal
    UnionFind uf(N);
    sort(edges.begin(), edges.end());
    long long res = 0;
    for (auto e : edges) {
        long long w = e.first;
        int u = e.second.first, v = e.second.second;
        if (uf.issame(u, v)) continue;
        res += w;
        uf.merge(u, v);
    }
    cout << res << endl;
}

解法 2: 辺を枝刈りして Kruskal 法

辺数を枝刈りする部分の発想は解法 1 と似ていますが、元のグラフがパスグラフであることを活かして、もっと積極的に枝刈りをします。最終的に枝数候補が $O(N)$ にまで減ります。

にあるものと同じ解法になります。以下のことが言えます。

$A_v$ が最大となる $v$ を考えたとき、 $v$ を一端点とする辺のうち

その左側に対してコスト最小の辺
その右側に対してコスト最小の辺

以外は無視していい

ということが言えます。そうすると、この性質から $A_v$ が大きい $v$ から順に、 $v$ の左右のコスト最小の辺 ( $v$ より $A_v$ が大きい頂点は除外) へと繋いでいけばいいことがわかります。

この性質もやはりサイクルの性質から示せます。今度は

$A_v$ が最大となる頂点 $v$
$v$ から見て左側の、辺コストが最小となる頂点 $u$
$v$ から見て左側の、それ以外の頂点 $w$

とを考えたとき、

辺 $vw$ の重み >= 辺 $vu$ の重み
辺 $vw$ の重み >= 辺 $uw$ の重み (この証明に $A_v$ の最大性を使う)

ということが言えます。よって $vw$ は不要です。計算量は $O(N\log{N})$ になります。

#include <iostream>
#include <vector>
#include <algorithm>
using namespace std;
template<class T> inline bool chmax(T& a, T b) { if (a < b) { a = b; return 1; } return 0; }
template<class T> inline bool chmin(T& a, T b) { if (a > b) { a = b; return 1; } return 0; }

// RMQ
template<class Monoid> struct RMQ {
    const Monoid INF;
    int SIZE_R;
    vector<pair<Monoid,int> > dat;
    
    RMQ(int n, const Monoid &inf): INF(inf) { init(n); }
    void init(int n) {
        SIZE_R = 1;
        while (SIZE_R < n) SIZE_R *= 2;
        dat.assign(SIZE_R * 2, pair<Monoid,int>(INF, -1));
    }
    
    /* set, a is 0-indexed */
    void set(int a, const Monoid &v) { dat[a + SIZE_R] = make_pair(v, a); }
    void build() {
        for (int k = SIZE_R - 1; k > 0; --k) {
            dat[k] = min(dat[k*2], dat[k*2+1]);
        }
    }
    
    /* update, a is 0-indexed */
    void update(int a, const Monoid &v) {
        int k = a + SIZE_R;
        dat[k] = make_pair(v, a);
        while (k >>= 1) dat[k] = min(dat[k*2], dat[k*2+1]);
    }
    
    /* get {min-value, min-index}, a and b are 0-indexed */
    pair<Monoid,int> get(int a, int b) {
        pair<Monoid,int> vleft = make_pair(INF, -1), vright = make_pair(INF, -1);
        for (int left = a + SIZE_R, right = b + SIZE_R; left < right; left >>= 1, right >>= 1) {
            if (left & 1) vleft = min(vleft, dat[left++]);
            if (right & 1) vright = min(dat[--right], vright);
        }
        return min(vleft, vright);
    }
    inline Monoid operator [] (int a) { return dat[a + SIZE_R].first; }
    
    /* debug */
    void print() {
        for (int i = 0; i < SIZE_R; ++i) {
            Monoid val = (*this)[i];
            if (val < INF) cout << val;
            else cout << "INF";
            if (i != SIZE_R-1) cout << ",";
        }
        cout << endl;
    }
};

// Union-Find
struct UnionFind {
    vector<int> par;
    
    UnionFind(int n) : par(n, -1) { }
    void init(int n) { par.assign(n, -1); }
    
    int root(int x) {
        if (par[x] < 0) return x;
        else return par[x] = root(par[x]);
    }
    
    bool issame(int x, int y) {
        return root(x) == root(y);
    }
    
    bool merge(int x, int y) {
        x = root(x); y = root(y);
        if (x == y) return false;
        if (par[x] > par[y]) swap(x, y); // merge technique
        par[x] += par[y];
        par[y] = x;
        return true;
    }
    
    int size(int x) {
        return -par[root(x)];
    }
};

using pint = pair<int,int>;
using Edge = pair<long long,pint>;

// 入力
int N;
long long D;
vector<pair<long long, int> > A;

int main() {
    cin >> N >> D;
    A.resize(N);
    RMQ<long long> left(N, 1LL<<60), right(N, 1LL<<60);
    for (int i = 0; i < N; ++i) {
        long long a; cin >> a; A[i] = make_pair(a, i);
        left.set(i, A[i].first - D * i);
        right.set(i, A[i].first + D * i);
    }
    left.build(), right.build();
    sort(A.begin(), A.end(), greater<pair<long long,int> >());
    
    // A[v] が大きい法から順に
    vector<Edge> edges;
    for (int i = 0; i < N; ++i) {
        int p = A[i].second;
        auto le = left.get(0, p);
        auto ri = right.get(p + 1, N);
        if (le.second != -1) edges.push_back(Edge(A[i].first + D * p + le.first, pint(p, le.second)));
        if (ri.second != -1) edges.push_back(Edge(A[i].first - D * p + ri.first, pint(p, ri.second)));
        left.update(p, 1LL<<60);
        right.update(p, 1LL<<60);
    }
    
    // Kruskal
    UnionFind uf(N);
    sort(edges.begin(), edges.end());
    long long res = 0;
    for (auto e : edges) {
        long long w = e.first;
        int u = e.second.first, v = e.second.second;
        if (uf.issame(u, v)) continue;
        res += w;
        uf.merge(u, v);
    }
    cout << res << endl;
}

解法 3: Borůvka 法

Tree MST の想定もこれだったし、ドワコン C - Interval and MST も Borůvka 法が自然にハマる。

今回も Borůvka 法でやると自然に解けるみたい。

解法 4: 賢い Prim 法

hogloid さんのツイート

解法 5: グラフ上 Vornoi 図

なんといっても

とこはるさんの記事

を参考に。この問題の一般化である Tree MST (元のグラフがパスからツリーに拡張) どころか、さらに一般のグラフに対しても適用できる解法。

けんちょんの競プロ精進記録

競プロの精進記録や小ネタを書いていきます

キーエンスプログラミングコンテスト 2019 E - Connecting Cities (橙色, 600 点)