Euclid の互除法な操作過程をたっぷりと味わえる味わい深い問題。

問題概要

一辺の長さが $N$ の正三角形の図のような $X$ の地点からビームを発射する。このとき、既にビームが通ったところは新たに壁になる。ビームは必ず元の場所に戻ることが証明できる。

ビームの通る長さを求めよ。

f:id:drken1215:20190315200825p:plain

制約

$2 \le N \le 10^{12}$

考えたこと

手続きが Eulcid の互除法っぽいというのが見て取れる。こういうのは、適切に部分問題を抜き取るのが難しい。

少し観察してみると、最初に 2 本 (合計長さ $N$ ) を通ってからは、下図のように

平行四辺形からひし形を切り落として、小さな平行四辺形にする

という感じになっていることがわかる。

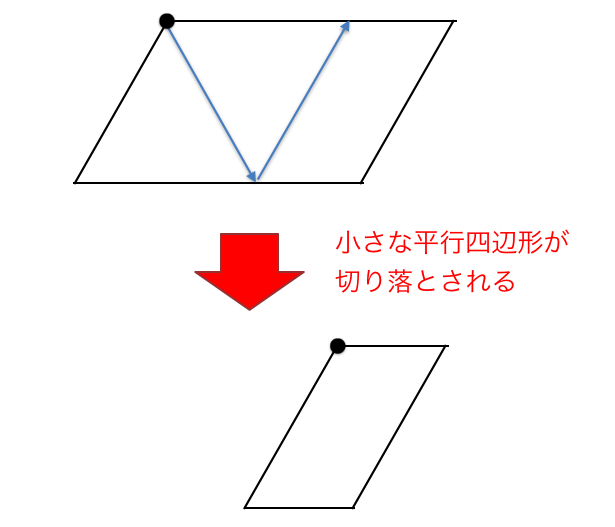
f:id:drken1215:20190315202814p:plain

この手続きが Euclid の互除法における

${\rm GCD}(a, b) = {\rm GCD}(a - b, b)$

という手続きに対応している。問題の例で言えば、 $N = 5, X = 2$ であり、

最初に 2 本 
→ 各辺が (3, 2) の平行四辺形 (ここまでの軌跡は 2 + 3 = 5)
→ 各辺が (1, 2) の平行四辺形 (軌跡は 2 × 2 = 4)
→ 各辺が (1, 1) の平行四辺形 (軌跡は 1 × 2 = 2)
→ その対角線を通って終わり (軌跡は 1)

という感じで合計 12 になっている。他の例として例えば $N = 78, X = 12$ とすると、2 本通った後に残る平行四辺形は、

最初に 2 本
→ 各辺が (66, 12) の平行四辺形 (ここまでで、66 + 12 = 78)
→ (54, 12) (12 × 2 = 24)
→ (42, 12) (12 × 2 = 24)
→ (30, 12) (12 × 2 = 24)
→ (18, 12) (12 × 2 = 24)
→ (6, 12) (12 × 2 = 24)
→ (6, 6) (6 × 2 = 12)
→ その対角線を通って終わり (6)

という感じになっている。ますます Euclid の互除法の雰囲気が出て来た。上で何度も 12 × 2 = 24 を足しているところは、以下のようにまとめてしまうことができる:

(66, 12) からは、66 = 12 × 5 + 6 より、長さ 12 のひし形を 5 回切り取ることになるので、(12 × 2) × 5 = 120 を加算して、残るのは (6, 12) の平行四辺形である

ここまでくると、Euclid の互除法のループを回しながら、軌跡を集計できることがハッキリして来る。そのままコードにすることで、 $O(\log{N})$ で求められる。

#include <iostream>
using namespace std;

int main() {
    long long N, X; cin >> N >> X;
    long long res = N; // 最初の 2 本の合計の長さ
    long long a = max(N - X, X), b = min(N - X, X); // 最初の 2 本の平行四辺形

    // Euclid の互除法を非再帰で回してみる
    while (b) {
        long long q = a / b;
        long long r = a % b;

        res += (b * 2) * q; // 答えを加算
        if (r == 0) res -= b; // 最後だけ「対角線」のみになるので
            
        a = b, b = r; // 次の平行四辺形は (b, r)
    }
    cout << res << endl;
}