「横移動 + 縦移動」で行けるところをすべて求めるのは簡単だし、「縦移動 + 横移動」で行けるところをすべて求めるのも簡単。しかし、両方の方法で行けるマスの扱いが難しい。

問題へのリンク

問題概要

$H \times W$ のグリッドがあり、そのうちの $M$ 個のマスは壁になっている (それ以外は通路)。

左上のマスからスタートして、以下の移動を 2 回以下実施することで到達できるマスの個数を求めよ。

壁にぶつからない限り、左方向に好きな量だけ移動する
壁にぶつからない限り、右方向に好きな量だけ移動する
壁にぶつからない限り、上方向に好きな量だけ移動する
壁にぶつからない限り、下方向に好きな量だけ移動する

制約

$H, W, M \le 2 \times 10^{5}$

考えたこと

とりあえず様子を掴んでみる。たとえば下図のような盤面で、

横に移動してから、縦に移動する
縦に移動してから、横に移動する

という 2 パターンのそれぞれについて、行けるところを考えてみる。

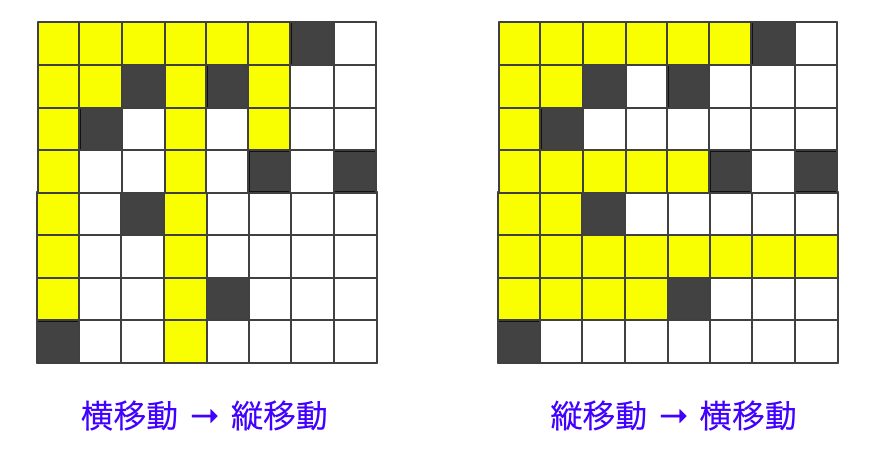
これらをそれぞれ数えることは簡単。次のような配列を持っておけばできる。

yoko[ r ] := r 行目において、(r, c) が壁であるような最小の c (r 行目に壁がないときは W)
tate[ c ] := c 列目において、(r, c) が壁であるような最小の r (c 行目に壁がないときは H)

これらを管理しておけば、数えられる。問題なのは、「横→縦」と「縦→横」の両パターンで行けるマスがあるので、その重複を除外する部分だ。

「縦→横」で行けるマスのうち、「横→縦」で行けないマス

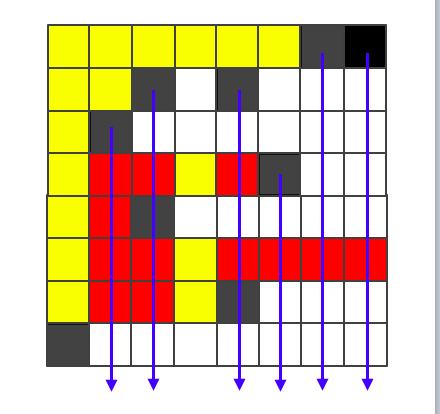
そこで、「縦→横」で行けるマスのうち、「横→縦」では行けないマスを数え上げることにしよう。図示すると、下図の赤マスがそれに該当する。

具体的には、下図のように、

まず、最上段については、壁が右詰めされているものとみなす
そして、上から下へと見ていったときに、壁に遮られた後のマスへは到達できない

と考えられる。これは BIT を用いて管理できる。

具体的には $W$ マスからなる BIT を用意して、各マスは「すでに壁に遮られなら 1」「まだ壁に遮られていないなら 0」を表すようにする。このとき、各 r = 0, 1, ..., H-1 に対して、次のようにすれば OK。

r 行目において、「縦→横」では行けるが「横→縦」では行けないマスの個数は、bit.sum(0, yoko[r]) と表せる
r 行目に壁 (r, c) が存在するとき、bit.sum(c, c+1) の値が 0 であるならば、bit.add(r, 1) を実施する

以上をまとめて、計算量は $O((H + W) \log W)$ になる。

コード

#include <bits/stdc++.h>
using namespace std;

template <class Abel> struct BIT {
    Abel UNITY_SUM = 0;
    vector<Abel> dat;
    
    // [0, n)
    BIT(int n, Abel unity = 0) : UNITY_SUM(unity), dat(n, unity) { }
    void init(int n) {
        dat.assign(n, UNITY_SUM);
    }
    
    // a is 0-indexed
    inline void add(int a, Abel x) {
        for (int i = a; i < (int)dat.size(); i |= i + 1)
            dat[i] = dat[i] + x;
    }
    
    // [0, a), a is 0-indexed
    inline Abel sum(int a) {
        Abel res = UNITY_SUM;
        for (int i = a - 1; i >= 0; i = (i & (i + 1)) - 1)
            res = res + dat[i];
        return res;
    }
    
    // [a, b), a and b are 0-indexed
    inline Abel sum(int a, int b) {
        return sum(b) - sum(a);
    }
    
    // debug
    void print() {
        for (int i = 0; i < (int)dat.size(); ++i)
            cout << sum(i, i + 1) << ",";
        cout << endl;
    }
};

int main() {
    int H, W, M;
    cin >> H >> W >> M;
    vector<vector<int>> yoko(H, vector<int>({W})), tate(W, vector<int>({H}));
    for (int i = 0; i < M; ++i) {
        int x, y; cin >> x >> y; --x, --y;
        yoko[x].push_back(y);
        tate[y].push_back(x);
    }
    for (int i = 0; i < H; ++i) sort(yoko[i].begin(), yoko[i].end());
    for (int j = 0; j < W; ++j) sort(tate[j].begin(), tate[j].end());

    // 横 → 縦
    long long res = 0;
    for (int j = 0; j < yoko[0][0]; ++j) res += tate[j][0];

    // 縦 → 横のうち、横 → 縦で行けないところ
    BIT<int> bit(W+1);
    for (int j = yoko[0][0]; j < W; ++j) bit.add(j, 1);
    for (int i = 0; i < tate[0][0]; ++i) {
        res += bit.sum(0, yoko[i][0]);
        for (auto y : yoko[i]) if (bit.sum(y, y+1) == 0) bit.add(y, 1);
    }
    cout << res << endl;
}