AtCoder ABC 246 F - typewriter (青色, 500 点)

包除原理を学べる問題！

• 問題へのリンク

問題概要

個の文字列 が与えられます。次の手順によって作れる長さ の文字列の個数を 998244353 で割ったあまりを求めてください。

1. のいずれかを選ぶ
2. 文字列 に含まれる文字のみを使って、長さ の文字列を作る

制約

• 
• 

包除原理へ

たとえば 、 で文字列が "ab"、"ac" である場合は

• "ab" から作れるのは、"aa", "ab", "ba", "bb" の 4 通り
• "ac" から作れるのは、"aa", "ac", "ca", "cc" の 4 通り
• 両方から作れるのは、"aa" の 1 通り

ということで、4 + 4 - 1 = 7 通りと求められます。より一般に の場合は、

(S[0] から作れる文字列の個数)
+ (S[1] から作れる文字列の個数)
- (S[0], S[1] の両方から作れる文字列の個数)

を計算すればよいことになります。

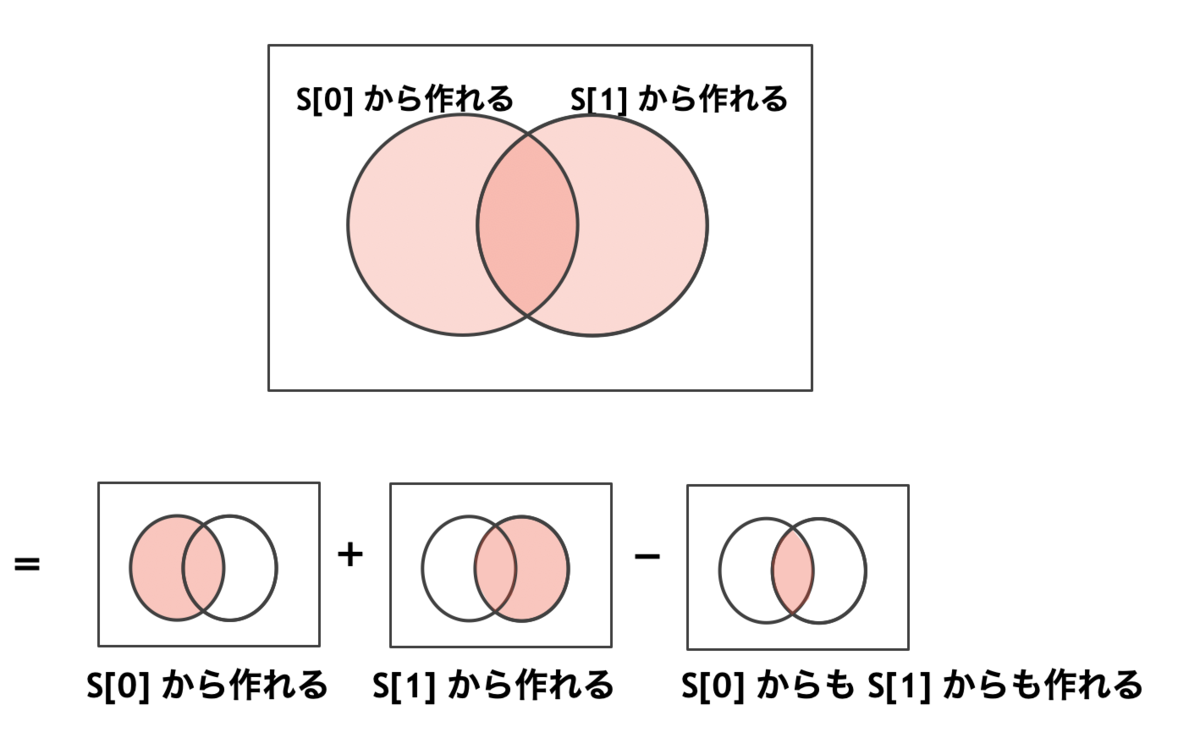
なお、S[0] から作れる文字列の個数は、S[0] に含まれる文字の種類数を として 通りとなります。

S[0], S[1] から作れる文字列の個数は、S[0] と S[1] にともに含まれる文字の種類数を として 通りとなります。

一般の の場合

の場合を拡張して、一般の の場合は次のように求められます。

---

文字列 の空でない部分集合 は 通り考えられる。そのそれぞれに対して、

• 集合 に含まれる文字列のいずれからも、作れる長さ の文字列の個数を としたとき
  • の要素数が奇数ならば を加算
  • の要素数が偶数ならば を減算

---

なお、 の計算は、 に含まれる文字列のすべてに含まれる文字の個数を として、

と計算できます。

コード

計算量は、各部分集合 に対して

• すべてに含まれる文字の個数 の計算：
• の計算：

ですので、全体として となります。

#include <bits/stdc++.h>
using namespace std;

const int MOD = 998244353;
long long modpow(long long a, long long n, long long mod) {
    long long res = 1;
    while (n > 0) {
        if (n & 1) res = res * a % mod;
        a = a * a % mod;
        n >>= 1;
    }
    return res;
}

int main() {
    int N, L;
    cin >> N >> L;
    vector<int> S(N, 0);
    for (int i = 0; i < N; ++i) {
        string str;
        cin >> str;
        for (char c : str) S[i] |= 1 << (c - 'a');
    }

    long long res = 0;
    for (int bit = 1; bit < (1 << N); ++bit) {
        int tmp = (1 << 26) - 1;
        for (int i = 0; i < N; ++i) {
            if (bit & (1 << i)) tmp &= S[i];
        }
        int m = __builtin_popcount(tmp);
        long long mL = modpow(m, L, MOD);

        if (__builtin_popcount(bit) & 1) res = (res + mL) % MOD;
        else res = (res + MOD - mL) % MOD;
    }
    cout << res << endl;
}