0. はじめに

bit 全探索は、世の中で「AtCoder 温室育ちだと弱い」と言われるタイプの問題の代表かもしれません。何も考えずに思考停止して全探索すればよいのですが、ちょっと実装が重たい傾向にあって、書き切るのが大変という感じです。difficulty を見ても ABC-C の中でも高めの傾向です。

bit 全探索の考え方や実装は、以下の記事にまとめてみました。

drken1215.hatenablog.com

しかし、全探索アルゴリズムにおいて、より汎用的な方法として再帰関数を用いるというのがあります。むしろ、再帰関数を自在に書きこなせるならば、bit 全探索を覚える必要はないかもしれないです。

そこで今回は、bit 全探索で定番の「部分和問題」を再帰関数で解いてみます。一口に「再帰で解く」といっても意外と書き方がたくさんあります。細かい違いを無視すると、ざっくり以下の 2 種類でしょうか...

情報を配っていく書き方
情報を集めていく書き方

これらの違いは、それほど本質ではないかもしれませんが、強いて言えば後者の方がメモ化によって DP にしやすいかなと思います。

1. 部分和問題

bit 全探索の例としてあまりにも有名な問題です。DP の練習でも出る問題ですね。

基本的には、各整数について「選ぶ」「選ばない」という 2 通りずつの選択肢があるので、調べるべき場合の数は

$2 \times 2 \times \dots \times 2 = 2^{N}$ 通り

ということになります。

問題概要

$N$ 個の正の整数 $a_{0}, a_{1}, \dots, a_{N-1}$ と、正の整数 $W$ とが与えられます。

$a_{0}, a_{1}, \dots, a_{N-1}$ の中から何個か選んで総和を $W$ とすることができるかどうかを判定してください。

制約

$1 \le N \le 20$

2. 情報を配っていく書き方

ひょっとしたら「部分和問題を再帰関数を使って解け」と言われたら、多くの方がこの書き方をするかもしれません。

文字通り、 $2^{N}$ 通りの合計値をすべて算出し、その中に $W$ が含まれるかどうかをチェックする考え方です。たとえば

$N = 3$
$W = 10$
$a = (2, 3, 8)$

の場合、下図のような感じです。

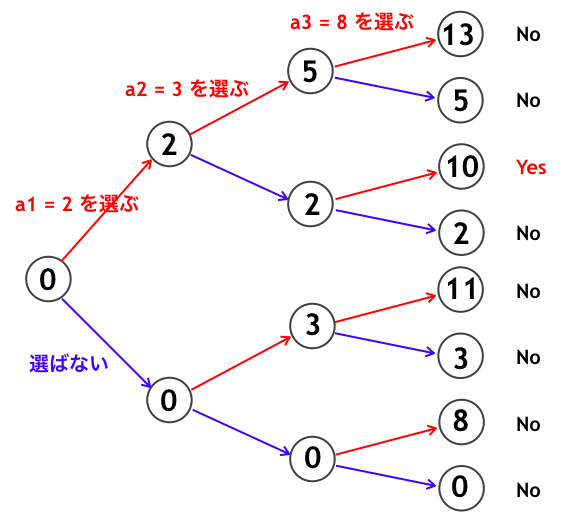
この様子を再帰関数を用いて実装すると、次のように書けるでしょう。sum という変数に「今までの情報」が込められていて、それを未来へと配っていくイメージです。計算量は $O(N2^{N})$ になります。

#include <iostream>
#include <vector>
using namespace std;

// 入力
int N, W;
vector<int> a;

bool rec(int i, int sum) {
    // 最終チェック
    if (i == N) {
        if (sum == W) return true;
        else return false;
    }
    
    // 選ぶ場合を分岐
    if (rec(i + 1, sum + a[i])) return true;

    // 選ばない場合を分岐
    if (rec(i + 1, sum)) return true;

    // どちらもダメ
    return false;
}

int main() {
    cin >> N >> W;
    a.resize(N);
    for (int i = 0; i < N; ++i) cin >> a[i];

    // 解く
    if (rec(0, 0)) cout << "Yes" << endl;
    else cout << "No" << endl;
}

注意

この書き方は自然なのですが、もう少し複雑な問題に対する複雑な実装になると、メモ化しづらくなる傾向にある気がします。そのあたりの事情は、診断人さんがリアリティ溢れる感情とともに綴っています。

動的計画法が苦手な人が、動的計画法が超苦手な人へアドバイスしてみる

この「配る書き方」は、動的計画法よりも、枝刈り探索をする場合に有効なイメージがあります。

3. 情報を集めていく書き方

より動的計画法に近い考え方になります。元の問題を部分問題に分解して、それらの解を用いて元の問題に答える感じイメージです！！！

どうやって問題を分割したらよいでしょうか。コツは「場合分けを意識すること」です。今回の部分和問題では、以下の 2 つの場合に分けて考えてみましょう。

$a_{0}$ を選ぶ場合
$a_{0}$ を選ばない場合

前者の場合、実は、「 $N-1$ 個の整数 $a_{1}, \dots, a_{N-1}$ の中からいくつか選んで総和を $W - a_{0}$ にすることは可能か？」という部分問題になるわけですね。後者は、「 $N-1$ 個の整数 $a_{1}, \dots, a_{N-1}$ の中からいくつか選んで総和を $W$ にすることは可能か？」という部分問題になります。

こうして、元の問題は 2 つの部分問題に分解されました！！！
元の問題は $N$ 個の整数に関する問題でしたが、部分問題はそれぞれ $N-1$ 個の整数に関する問題です。これらの部分問題を再帰関数に押し付けて、再帰的に解いていくわけです。そしてその部分問題の答えをまとめあげて、元の問題の答えを作り上げていきます。今回であれば、

2 つの部分和問題のうち、少なくとも一方が Yes ならば、元の問題の答えも Yes
2 つの部分和問題のうち、どちらの答えも No ならば、元の問題の答えも No

ということになります。

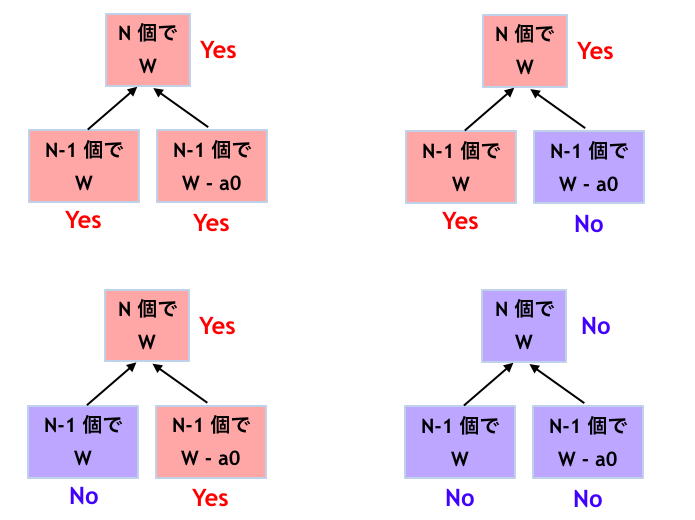
さて、 $N$ 個の整数に関する問題が $N-1$ 個の整数に関する部分問題へと分解されました。それらを今度は $N-2$ 個の整数に関する部分問題へと分解していきます。

一般に、 $i$ 個の整数に関する問題を、 $i-1$ 個の整数に関する 2 つの問題に分解して、まとめあげるようにします。たとえば

$N = 3$
$W = 10$
$a = (2, 3, 8)$

の場合、全体のイメージは下図のような感じです。

つまり、「 $N$ 個の整数に関する問題」が分解されていくうちに徐々に小さくなって、最後は「 $0$ 個の整数に関する問題」になります。 $0$ 個の整数の総和は $0$ にしかならないので、

$0$ を作る問題なら Yes
$0$ 以外を作る問題なら No

となります。この情報を上へ上へと伝播していき、最終的に元の問題の答えが求まります。以上を実装すると、次のように書けます。計算量は $O(N2^{N})$ になります。

#include <iostream>
#include <vector>
using namespace std;

// 入力
int N, W;
vector<int> a;

// a[i], a[i+1], ..., a[N-1] の総和を w にできるか？
bool rec(int i, int w) {
    // 最終チェック
    if (i == N) {
        if (w == 0) return true;
        else return false;
    }
    
    // 選ぶ場合を分岐
    if (rec(i + 1, w - a[i])) return true;

    // 選ばない場合を分岐
    if (rec(i + 1, w)) return true;

    // どちらもダメ
    return false;
}

int main() {
    cin >> N >> W;
    a.resize(N);
    for (int i = 0; i < N; ++i) cin >> a[i];

    // 解く
    if (rec(0, W)) cout << "Yes" << endl;
    else cout << "No" << endl;
}

後ろからやる

細かい違いなのですが、上の再帰関数では「部分問題の切り出し方」とは

$a_{i}, a_{i+1}, \dots, a_{N-1}$ の総和を $w$ にできるか

という風な感じでした。なんとなく不自然な気もします。むしろ、次のようにすることが多いように思います。

【より自然な部分問題】
$a_{0}, a_{1}, \dots, a_{i-1}$ の総和を $w$ にできるか

こういう風に書き直してみましょう。

#include <iostream>
#include <vector>
using namespace std;

// 入力
int N, W;
vector<int> a;

// a[0], a[1], ..., a[i-1] の総和を w にできるか？
bool rec(int i, int w) {
    // 最終チェック
    if (i == 0) {
        if (w == 0) return true;
        else return false;
    }
    
    // 選ぶ場合を分岐
    if (w >= a[i - 1] && rec(i - 1, w - a[i-1])) return true;

    // 選ばない場合を分岐
    if (rec(i - 1, w)) return true;

    // どちらもダメ
    return false;
}

int main() {
    cin >> N >> W;
    a.resize(N);
    for (int i = 0; i < N; ++i) cin >> a[i];

    // 解く
    if (rec(N, W)) cout << "Yes" << endl;
    else cout << "No" << endl;
}

メモ化すると DP

さきほどの実装はこのままでは $O(N2^{N})$ です。しかしほんのちょっとの工夫によって、なんと DP になってしまいます！！！再帰関数の定義は

rec(i, w) := $a_{0}, a_{1}, \dots, a_{i-1}$ の総和を $w$ にできるか

でした。この答えをメモするのです。そうすると以下のような実装になります。この計算量は $O(NW)$ です！

#include <iostream>
#include <vector>
using namespace std;

// 入力
int N, W;
vector<int> a;

// a[0], a[1], ..., a[i-1] の総和を w にできるか？
vector<vector<int>> dp; // -1: 未求、0: No、1; Yes
int rec(int i, int w) {
    // メモをチェック
    if (dp[i][w] != -1) return dp[i][w];
    
    // 最終チェック
    if (i == 0) {
        if (w == 0) return true;
        else return false;
    }

    // 再帰的に求める
    int res = 0;
    if (w >= a[i - 1] && rec(i - 1, w - a[i-1]) == 1) res = 1;
    if (rec(i - 1, w) == 1) res = 1;

    // メモしながら返す
    return dp[i][w] = res;
}

int main() {
    cin >> N >> W;
    a.resize(N);
    for (int i = 0; i < N; ++i) cin >> a[i];

    // 解く
    dp.assign(N+1, vector<int>(W+1, -1)); // -1 で初期化
    if (rec(N, W) == 1) cout << "Yes" << endl;
    else cout << "No" << endl;
}

4. まとめ

bit 全探索は一つの登竜門になっているイメージがあります。もちろんビット列を自在に使いこなせることはとても重要です。しかしそれ以上に、汎用的な再帰関数を自在に使いこなせることが重要かなと思います。再帰関数を用いた探索が自在に使えると、動的計画法にもつながります！！！

けんちょんの競プロ精進記録

競プロの精進記録や小ネタを書いていきます

bit 全探索を「再帰関数」で書く 2 つの流儀