これは天才!!!
問題概要
一直線上に 個の点が順に並んでいる (座標が
)。
個のクエリが与えられる。
- 各クエリでは区間
(
) が与えられる
個の点のうち
のみを取り出してできる
個の点について以下の問に答えよ
- 与えられた点集合から、どの 2 点の距離も
以上となるように選ぶ最大個数を
とする
- 与えられた点集合から、どの 2 点の距離も
以上となるように
個選ぶ方法をすべて考えたとき、それらのうちの少なくとも 1 つ以上の選ばれる点集合に含まれるような点の個数を求めよ
- 与えられた点集合から、どの 2 点の距離も
制約
考えたこと
いわゆる「最適解に含まれうる要素を列挙する」というタイプの問題。そしてこういうクエリに大量に答える系の問題では、まずは 1 つのクエリのみに答える方法を考えて、それを高速化する方法を考えていく。
まず最適解を一つ求めるだけならば Greedy にやれば OK。
- 点
を採用する
を満たす最小の
を採用する
- これを
となるまで繰り返す
ある点 が最適解に含まれうるかどうかは、愚直には次のように判定できる。最大個数を
とする。
を採用する
- 左右それぞれについて距離
以上離れた部分についての問題を解く
- 合計値が
となれば
は最適解に含まれうる点であるといえる
左右両端から Greedy
以上の考察から、点 およびそこからの距離が
未満の点を取り除いた区間に関する問題を素早く解きたいということになる。よって、
- 区間
に関する最適個数
- 区間
に関する最適個数
をそれぞれ前処理したくなる。これを前処理しておくことで、1 つの区間に関するクエリに対する解は、各点に対して で判定できるので、
の計算量となる。しかしこれを各クエリに対して実施したのでは
となって間に合わない。高速化が必要となる。
各点が最適解に含まれうるかどうかの条件をさらにわかりやすく特徴づけ
各点が最適解に含まれうるかどうかの判定を効率化するために、さらにわかりやすく特徴付けることを考える (ここから先はできなかった)。
下図のように、左右両端からの Greedy 解が得られているとする。左からの Greedy 点の添字を とし、右からの Greedy 点の添字を (左から)
とする。このとき、
となるような
はダメ
- このとき
も
も採用できないため、
点選ぶことはできない
- このとき
となるような
は OK
の左側は
系列からとり、右側は
系列からとれば OK
ということがわかる。
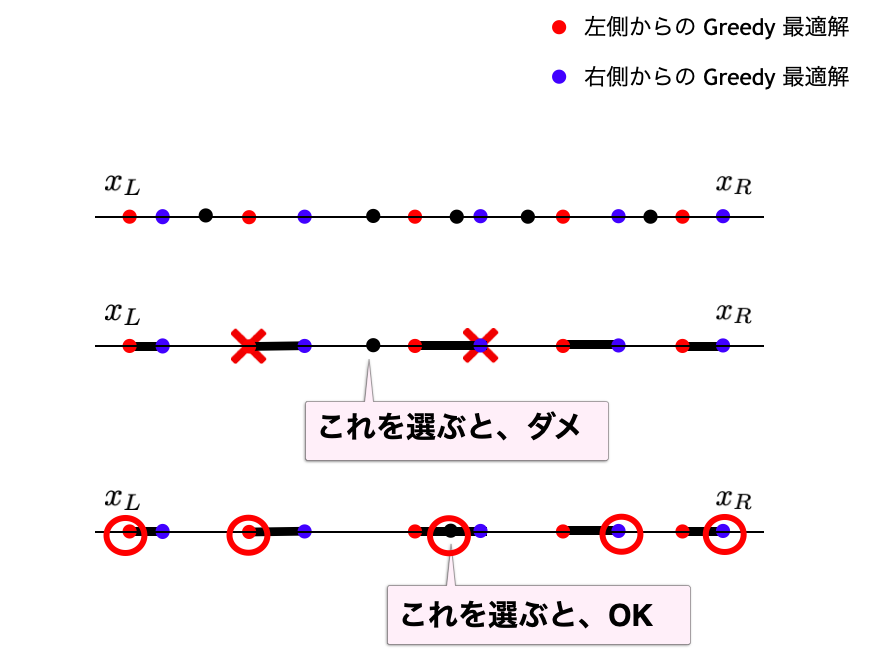
以上から、各点が最適解に含まれうるかどうかを判定するためのわかりやすい特徴づけが得られた。最後にこの特徴づけに基づいた数え上げ方法を考える。
上図の太線区間に含まれる点の個数を数えることができればよい。これは、
と求められる。
ダブリングへ
区間クエリに素早く答えるようにするための前処理として、ダブリングはとても有効。
- next[ d ][ v ] := 点
から右側へと Greedy にとっていったとき、
個先の点
- nsum[ d ][ v ] := 点
から右側へと Greedy にとっていったとき、
個分の添字の総和
- prev[ d ][ v ] := 点
から左側へと Greedy にとっていったとき、
個前の点
- psum[ d ][ v ] := 点
から左側へと Greedy にとっていったとき、
個分の添字の総和
を求めることで、各クエリに で答えられる。以上をまとめると計算量は
となる。
#include <bits/stdc++.h> using namespace std; template<class T> inline bool chmax(T& a, T b) { if (a < b) { a = b; return 1; } return 0; } template<class T> inline bool chmin(T& a, T b) { if (a > b) { a = b; return 1; } return 0; } const int MAX = 30; const long long INF = 1LL<<55; int main() { int N, Q; long long K; cin >> N >> K; vector<long long> X(N+2, -INF); for (int i = 1; i <= N; ++i) cin >> X[i]; X[N+1] = INF; // doubling vector<vector<long long>> next(MAX+1, vector<long long>(N+2, N+1)); vector<vector<long long>> nsum(MAX+1, vector<long long>(N+2)); vector<vector<long long>> prev(MAX+1, vector<long long>(N+2, 0)); vector<vector<long long>> psum(MAX+1, vector<long long>(N+2)); for (int i = 1; i <= N; ++i) { next[0][i] = lower_bound(X.begin(), X.end(), X[i]+K) - X.begin(); prev[0][i] = (int)(upper_bound(X.begin(), X.end(), X[i]-K) - X.begin()) - 1; nsum[0][i] = psum[0][i] = i; } for (int d = 0; d < MAX; ++d) { for (int i = 1; i <= N; ++i) { next[d+1][i] = next[d][next[d][i]]; prev[d+1][i] = prev[d][prev[d][i]]; nsum[d+1][i] = nsum[d][i] + nsum[d][next[d][i]]; psum[d+1][i] = psum[d][i] + psum[d][prev[d][i]]; } } // query cin >> Q; while (Q--) { int L, R; cin >> L >> R; int left = L, right = R; long long num = 0, leftsum = 0, rightsum = 0; for (int d = MAX; d >= 0; --d) { if (next[d][left] > R) continue; num += (1LL<<d); leftsum += nsum[d][left]; rightsum += psum[d][right]; left = next[d][left]; right = prev[d][right]; } ++num, leftsum += left, rightsum += right; long long res = rightsum - leftsum + num; cout << res << endl; } }