けんちょんの競プロ精進記録

競プロの精進記録や小ネタを書いていきます

JOI 予選 2016 D - JOI国のお散歩事情 (AOJ 0622, 難易度 6)

JOI JOI予選 JOI難易度6 AtCoder AOJ 最適化テク:最適解の形を考える テク:区間ごとに分割する 一直線上のN点の問題 各kに対して 番兵法 二分探索 二分探索:lower_bound 最適化テク:探索候補を絞る 点が移動していく問題 操作後の結果を求める問題

手を動かしてみると、どうなってるかが見えてくる！

問題概要

N 人がそれぞれ座標 A_{1}, \dots, A_{N} に並んでいる (単調増加、負もありうる、各 A_{i} は偶数)。そして時刻 0 において、 N 人はそれぞれ正の方向 ( D_{i} = 1 で与えられる) または負の方向 ( D_{i} = 2 で与えられる) に 1 秒間に 1 のペースで歩き始める。

ただし、ある 2 人が出くわしたとき、2 人ともその場で永久にストップする。その後別の人が、その地点に訪れた場合、その人もその場で永久にストップする。

T 秒後の世界において、 X_{1}, \dots, X_{Q} 番目の人がいる座標を求めよ ( Q 人が指定される)。

制約

  • 1 \le N \le 10^{5}
  • 1 \le Q \le \min(N, 1000)
  • 0 \le T \le 10^{18}

考えたこと

この手の問題はまずは手を動かすとよさそうなのと、極端な場合を考えるとよさそう。つまり T がいくらでも大きくなった世界ではどんなふうになるのかを考察してみる。

そうすると下図のようになる。無限時間経過したあとでは

  • 左側にいる「1」の人たちは、ずっと左に向かい続けている
  • 右側にいる「2」の人たちは、ずっと右に向かい続けている
  • それ以外の人は、下図の紫点線の位置に集結する

というふうになっていることがわかる。

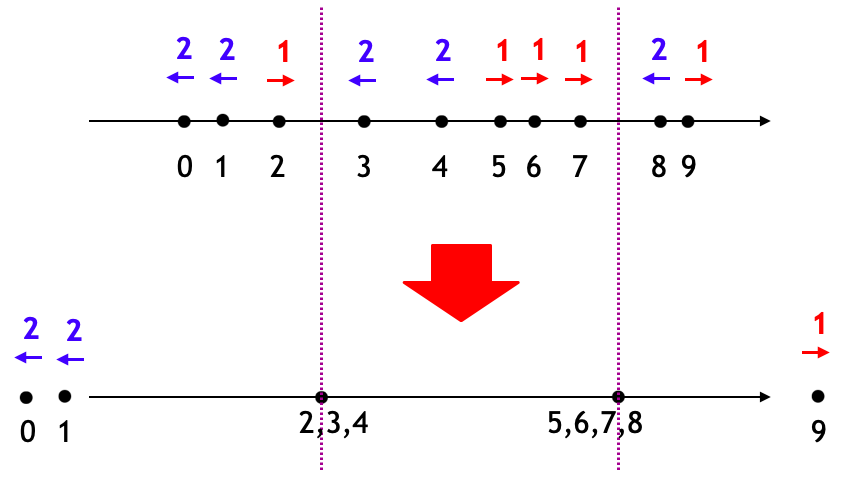
f:id:drken1215:20201128194722p:plain

図の紫点線の位置は「1 の人と 2 の人との境界」に位置する。

有限時間 T 秒後の場合

無限時間経過した場合を考えてみたけど、これがわかっていれば T 秒後の状態もすぐにわかる。

たとえば、 A_{i} の位置をスタートして右に行く人を考える (左に行く人も同様)。そしてその人から見て最寄りの「紫点線」の境界が C であったとする。このとき T 秒後の位置は

\min(A_{i} + T, C)

と求められる。最寄りの「紫点線」の位置は、二分探索法 (lower_bound) や、しゃくとり法を用いることで高速に求められる。

コード

ここでは二分探索法を用いた。計算量は O(N + Q \log N) となる。

また、「紫点線」の座標を表す変数 col において、両端点に番兵 (-INF と INF) を挿入した

#include <bits/stdc++.h>
using namespace std;

const long long INF = 1LL<<60;
int main() {
    long long N, T, Q;
    cin >> N >> T >> Q;
    vector<long long> A(N), D(N);
    for (int i = 0; i < N; ++i) cin >> A[i] >> D[i];
    vector<long long> col;
    col.push_back(-INF);
    for (int i = 0; i+1 < N; ++i) {
        if (D[i] == 1 && D[i+1] == 2) col.push_back((A[i] + A[i+1])/2);
    }
    col.push_back(INF);

    for (int q = 0; q < Q; ++q) {
        int X; cin >> X; --X;
        if (D[X] == 1) {
            auto it = lower_bound(col.begin(), col.end(), A[X]);
            cout << min(*it, A[X] + T) << endl;
        }
        else {
            auto it = upper_bound(col.begin(), col.end(), A[X]);
            --it;
            cout << max(*it, A[X] - T) << endl;
        }
    }
}