問題概要

正の整数からなる整数列 $A_{1}, \dots, A_{N}$ が与えられる。以下の操作を好きなだけ行うことによって、 $N$ 個の値がすべて等しくなるようにしたい。

2 つの整数値 $x, y$ を選ぶ
整数列中の値 $x$ をすべて $y$ に書き換える

目的を達成できる操作回数として考えられる最小値を求めよ。

制約

$1 \le N, A_{i} \le 2 \times 10^{5}$

考えたこと

この問題の真のポイントは、Union-Find ガチャを回すことでも、グラフの問題だと気づくでもなく、自然な数学的考察を積み上げることなのかなと思う。

まずは具体的な様子を見てみよう。 $N = 11$ で $A = (6, 3, 1, 2, 7, 5, 3, 7, 1, 2, 4)$ としてみます。このとき、下図の「線」を引かれた両端は揃っている必要があります。

まず、真ん中の数値については何も考えなくてよいです ( $N$ が奇数の場合)。たとえ真ん中の数値がどこかの操作で変わったとしても、また他の数値がどのように変化したとしても、まったく気にする必要はないです。よって、真ん中の数値は無視しましょう。また同様に、「両端の数値が等しくなっている線の両端」についても、まったく気にする必要はないです。以上のことを加味すると、次のようになります。

さて、まず両端の 6 と 4 をくっつける必要がある。ここで 6 を 4 にしても、4 を 6 にしても、結局のところ変わらない。いずれにしても 6 と 4 をくっつける感じになる。この操作が Union-Find の merge っぽいな......という連想が働く。

ここで注意したいのは「両端を見て値が異なっている箇所を数える」というのは嘘解法ということだ。たとえば、上図の場合

6 と 4
3 と 2
2 と 7

までをマージした時点で、7 と 3 はマージされている (3 と 2、2 と 7 がそれぞれマージされているので 7 と 3 はマージされている)。よって上図の場合の答えは 4 回ではなく、3 回なのだ。

なんとなくだけど、Union-Find でひたすら merge していって、すでに merge されていたら merge はやめておいて、結局 merge した回数を答えればよいのでは...という想像が働く。結局それで正しくなる。

merge 回数より少ない回数でできない理由

ここで大事なことは、Union-Find の merge 回数よりも少ない回数ではダメだということをきちんと数学的に納得することだと思う。この納得感が得られるかどうかで、今後 AtCoder のより高度な問題を解く時に数学的直観が正しく働くかどうかが分かれる気がするのだ。

とりあえず、ここまで考えてきた具体例について、結びつくべき数値の関係性を図示すると、下図のようになる。

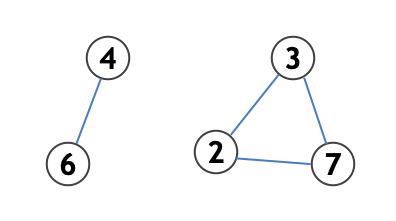
こうすると分かりやすい。一般に $K$ 個のノードをすべて連結にするには $K-1$ 本の辺が必要 (そして十分) なのだ ( $K$ 頂点の木の辺の本数は $K-1$ 本)。

ここまで来たら次の解法でよいことが確定する。

$A_{i}$ と $A_{N-i-1}$ の組を順番に見ていく
それらの値が異なっていて、かつ、Union-Find 上で同じグループでない場合には merge する

merge した回数が答えになる。

コード

計算量は $N \alpha(N)$ になる。

#include <bits/stdc++.h>
using namespace std;

struct UnionFind {
    vector<int> par;

    UnionFind() { }
    UnionFind(int n) : par(n, -1) { }
    void init(int n) { par.assign(n, -1); }
    
    int root(int x) {
        if (par[x] < 0) return x;
        else return par[x] = root(par[x]);
    }
    
    bool issame(int x, int y) {
        return root(x) == root(y);
    }
    
    bool merge(int x, int y) {
        x = root(x); y = root(y);
        if (x == y) return false;
        if (par[x] > par[y]) swap(x, y); // merge technique
        par[x] += par[y];
        par[y] = x;
        return true;
    }
    
    int size(int x) {
        return -par[root(x)];
    }
};

const int MAX = 210000;
int main() {
    int N;
    cin >> N;
    vector<int> A(N);
    for (int i = 0; i < N; ++i) cin >> A[i];

    UnionFind uf(MAX);
    for (int i = 0, j = N-1; i < j; ++i, --j) {
        uf.merge(A[i], A[j]);
    }
    long long res = 0;
    for (int v = 0; v < MAX; ++v) {
        if (uf.root(v) == v) {
            res += uf.size(v) - 1;
        }
    }
    cout << res << endl;
}