三乗の解法はすぐに出てくるので、それを上手に高速化する！

問題へのリンク

問題概要

$H \times W$ のグリッドが与えられる。"." マス (通路) には行けるが "#" マス (壁) には行けない。左上のマスから右下のマスへと行きたい。毎回のターンで以下のいずれかの行動をとることができる。

右方向に、壁にぶつからない範囲内で好きなマスへ移動できる
下方向に、壁にぶつからない範囲内で好きなマスへ移動できる
右下方向に、壁にぶつからない範囲内で好きなマスへ移動できる

左上から右下へと至る経路の本数を、1000000007 で割ったあまりを求めよ。

制約

$2 \le H, W \le 2000$

考えたこと

もし三乗 ( $O(HW(H+W)$ ) かけてよいのであれば、次のような DP でできる！！

dp[ r ][ c ] := マス (r, c) に至るまでの経路の本数

遷移は次のようにできる。

k = 1, 2, ... について dp[ r ][ c ] += dp[ r ][ c - k ]　(マス (r, c - k) が壁や場外になった時点で打ち切り)
k = 1, 2, ... について dp[ r ][ c ] += dp[ r - k ][ c ]　(マス (r - k, c) が壁や場外になった時点で打ち切り)
k = 1, 2, ... について dp[ r ][ c ] += dp[ r - k ][ c - k ]　(マス (r - k, c - k) が壁や場外になった時点で打ち切り)

1 個目の遷移は「左からやってくる方法」を数えていて、2 個目の遷移は「上からやってくる方法」を数えていて、3 個目の遷移は「左上からやってくる方法」を数えている。

とても自然な解法だけど、このままでは DP の状態量が $O(HW)$ だけあって、それぞれのマスの値を求めるのに $O(H+W)$ だけの遷移を考えることになるので、全部で $O(HW(H+W)$ の計算量となってしまう。

このままでは間に合わないので高速化方法を考える。

解法(1)：累積和

愚直な DP が間に合わないときに、累積和を活用することで高速化するのはめっちゃよく見る！！！最近だとこの問題もそう！！

atcoder.jp

今回は次のような「三種の累積和」を持つことにしよう！！！

X[ i ][ j ] := dp[ i ][ j ], dp[ i ][ j - 1 ], dp[ i ][ j - 2 ], ... の総和 (壁にぶつかったら打ち切り)
Y[ i ][ j ] := dp[ i ][ j ], dp[ i - 1 ][ j ], dp[ i - 2 ][ j ], ... の総和 (壁にぶつかったら打ち切り)
Z[ i ][ j ] := dp[ i ][ j ], dp[ i - 1 ][ j - 1 ], dp[ i - 2 ][ j - 2 ], ... の総和 (壁にぶつかったら打ち切り)

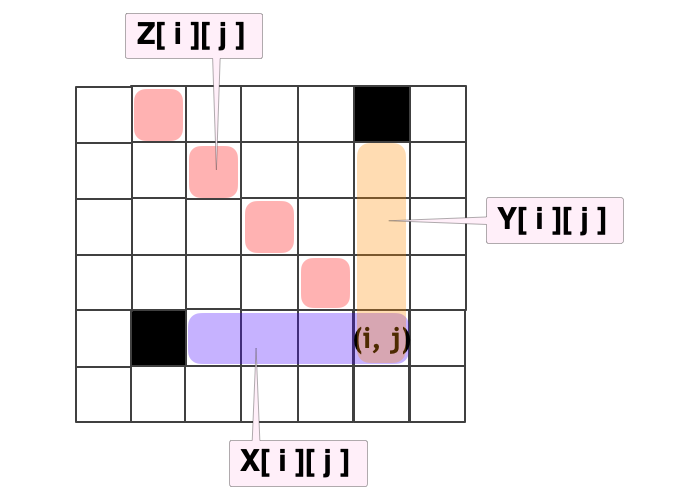
これを持っておくと、DP の遷移は次のようにできる。これで DP 遷移が $O(1)$ でできるようになった！！！

dp[i][j] += X[i][j-1]; // 左から来る場合
dp[i][j] += Y[i-1][j]; // 上から来る場合
dp[i][j] += Z[i-1][j-1]; // 左上から来る場合

dp[ i ][ j ] の値が確定したら、三種類の累積和 X, Y, Z をそれぞれ、次のように更新しておこう！！

X[i][j] = X[i][j-1] + dp[i][j];
Y[i][j] = Y[i-1][j] + dp[i][j];
Z[i][j] = Z[i-1][j-1] + dp[i][j];

全体として、計算量は $O(HW)$ となる。

コード

#include <bits/stdc++.h>
using namespace std;

// modint
template<int MOD> struct Fp {
    long long val;
    constexpr Fp(long long v = 0) noexcept : val(v % MOD) {
        if (val < 0) val += MOD;
    }
    constexpr int getmod() const { return MOD; }
    constexpr Fp operator - () const noexcept {
        return val ? MOD - val : 0;
    }
    constexpr Fp operator + (const Fp& r) const noexcept { return Fp(*this) += r; }
    constexpr Fp operator - (const Fp& r) const noexcept { return Fp(*this) -= r; }
    constexpr Fp operator * (const Fp& r) const noexcept { return Fp(*this) *= r; }
    constexpr Fp operator / (const Fp& r) const noexcept { return Fp(*this) /= r; }
    constexpr Fp& operator += (const Fp& r) noexcept {
        val += r.val;
        if (val >= MOD) val -= MOD;
        return *this;
    }
    constexpr Fp& operator -= (const Fp& r) noexcept {
        val -= r.val;
        if (val < 0) val += MOD;
        return *this;
    }
    constexpr Fp& operator *= (const Fp& r) noexcept {
        val = val * r.val % MOD;
        return *this;
    }
    constexpr Fp& operator /= (const Fp& r) noexcept {
        long long a = r.val, b = MOD, u = 1, v = 0;
        while (b) {
            long long t = a / b;
            a -= t * b, swap(a, b);
            u -= t * v, swap(u, v);
        }
        val = val * u % MOD;
        if (val < 0) val += MOD;
        return *this;
    }
    constexpr bool operator == (const Fp& r) const noexcept {
        return this->val == r.val;
    }
    constexpr bool operator != (const Fp& r) const noexcept {
        return this->val != r.val;
    }
    friend constexpr istream& operator >> (istream& is, Fp<MOD>& x) noexcept {
        is >> x.val;
        x.val %= MOD;
        if (x.val < 0) x.val += MOD;
        return is;
    }
    friend constexpr ostream& operator << (ostream& os, const Fp<MOD>& x) noexcept {
        return os << x.val;
    }
    friend constexpr Fp<MOD> modpow(const Fp<MOD>& r, long long n) noexcept {
        if (n == 0) return 1;
        if (n < 0) return modpow(modinv(r), -n);
        auto t = modpow(r, n / 2);
        t = t * t;
        if (n & 1) t = t * r;
        return t;
    }
    friend constexpr Fp<MOD> modinv(const Fp<MOD>& r) noexcept {
        long long a = r.val, b = MOD, u = 1, v = 0;
        while (b) {
            long long t = a / b;
            a -= t * b, swap(a, b);
            u -= t * v, swap(u, v);
        }
        return Fp<MOD>(u);
    }
};
const int MOD = 1000000007;
using mint = Fp<MOD>;

int main() {
    int H, W;
    cin >> H >> W;
    vector<string> fi(H);
    for (int i = 0; i < H; ++i) cin >> fi[i];

    vector<vector<mint>> dp(H+1, vector<mint>(W+1, 0)), X = dp, Y = dp, Z = dp;
    dp[1][1] = 1;
    for (int i = 1; i <= H; ++i) {
        for (int j = 1; j <= W; ++j) {
            // 壁だったらこれまでの累積和をリセット
            if (fi[i-1][j-1] == '#') {
                X[i][j] = Y[i][j] = Z[i][j] = 0;
                continue;
            }
            // 三方向からの累積和を合算
            dp[i][j] += X[i][j-1] + Y[i-1][j] + Z[i-1][j-1];
            
            // 累積和を更新
            X[i][j] = X[i][j-1] + dp[i][j];
            Y[i][j] = Y[i-1][j] + dp[i][j];
            Z[i][j] = Z[i-1][j-1] + dp[i][j];
        }
    }
    cout << dp[H][W] << endl;
}

解法(2)：DP に付加状態を持たせる

もう一つ上手い方法がある！！！次のように DP に付加状態を持たせる

dp[ i ][ j ][ k ] := マス (i, j) に至る方法のうち、方向 k から来た場合についての本数
- k = 0：左から来た場合
- k = 1：上から来た場合
- k = 2：左上から来た場合
res[ i ][ j ] := マス (i, j) に来る方法の個数 (= dp[ i ][ j ][ 0 ] + dp[ i ][ j ][ 1 ] + dp[ i ][ j ][ 2 ])

k = 0 の場合の状態遷移について、場合分けして考えてみる。

頂点 (i - 1, j) に一回立ち止まってから来る場合：res[ i - 1 ][ j ] 通り
頂点 (i - 1, j) を通らずに来る場合：dp[ i - 1 ][ j ][ 0 ] 通り

よって、

dp[ i ][ j ][ 0 ] += res[ i - 1 ][ j ] + dp[ i - 1 ][ j ][ 0 ]

となる。k = 1, 2 についても同様にできる。この方法でも計算量は $O(HW)$ となる。

コード

#include <bits/stdc++.h>
using namespace std;

// modint
template<int MOD> struct Fp {
    long long val;
    constexpr Fp(long long v = 0) noexcept : val(v % MOD) {
        if (val < 0) val += MOD;
    }
    constexpr int getmod() const { return MOD; }
    constexpr Fp operator - () const noexcept {
        return val ? MOD - val : 0;
    }
    constexpr Fp operator + (const Fp& r) const noexcept { return Fp(*this) += r; }
    constexpr Fp operator - (const Fp& r) const noexcept { return Fp(*this) -= r; }
    constexpr Fp operator * (const Fp& r) const noexcept { return Fp(*this) *= r; }
    constexpr Fp operator / (const Fp& r) const noexcept { return Fp(*this) /= r; }
    constexpr Fp& operator += (const Fp& r) noexcept {
        val += r.val;
        if (val >= MOD) val -= MOD;
        return *this;
    }
    constexpr Fp& operator -= (const Fp& r) noexcept {
        val -= r.val;
        if (val < 0) val += MOD;
        return *this;
    }
    constexpr Fp& operator *= (const Fp& r) noexcept {
        val = val * r.val % MOD;
        return *this;
    }
    constexpr Fp& operator /= (const Fp& r) noexcept {
        long long a = r.val, b = MOD, u = 1, v = 0;
        while (b) {
            long long t = a / b;
            a -= t * b, swap(a, b);
            u -= t * v, swap(u, v);
        }
        val = val * u % MOD;
        if (val < 0) val += MOD;
        return *this;
    }
    constexpr bool operator == (const Fp& r) const noexcept {
        return this->val == r.val;
    }
    constexpr bool operator != (const Fp& r) const noexcept {
        return this->val != r.val;
    }
    friend constexpr istream& operator >> (istream& is, Fp<MOD>& x) noexcept {
        is >> x.val;
        x.val %= MOD;
        if (x.val < 0) x.val += MOD;
        return is;
    }
    friend constexpr ostream& operator << (ostream& os, const Fp<MOD>& x) noexcept {
        return os << x.val;
    }
    friend constexpr Fp<MOD> modpow(const Fp<MOD>& r, long long n) noexcept {
        if (n == 0) return 1;
        if (n < 0) return modpow(modinv(r), -n);
        auto t = modpow(r, n / 2);
        t = t * t;
        if (n & 1) t = t * r;
        return t;
    }
    friend constexpr Fp<MOD> modinv(const Fp<MOD>& r) noexcept {
        long long a = r.val, b = MOD, u = 1, v = 0;
        while (b) {
            long long t = a / b;
            a -= t * b, swap(a, b);
            u -= t * v, swap(u, v);
        }
        return Fp<MOD>(u);
    }
};
const int MOD = 1000000007;
using mint = Fp<MOD>;

int main() {
    int H, W;
    cin >> H >> W;
    vector<string> fi(H);
    for (int i = 0; i < H; ++i) cin >> fi[i];

    vector<vector<vector<mint>>> dp(H+1, vector<vector<mint>>(W+1, vector<mint>(3, 0)));
    vector<vector<mint>> res(H+1, vector<mint>(W+1, 0));
    res[1][1] = 1;
    for (int i = 1; i <= H; ++i) {
        for (int j = 1; j <= W; ++j) {
            if (fi[i-1][j-1] == '#') continue;

            dp[i][j][0] += res[i][j-1] + dp[i][j-1][0];
            dp[i][j][1] += res[i-1][j] + dp[i-1][j][1];
            dp[i][j][2] += res[i-1][j-1] + dp[i-1][j-1][2];
            res[i][j] += dp[i][j][0] + dp[i][j][1] + dp[i][j][2];
        }
    }
    cout << res[H][W] << endl;
}

けんちょんの競プロ精進記録

競プロの精進記録や小ネタを書いていきます

AtCoder ABC 183 E - Queen on Grid (水色, 500 点)

問題概要

制約

考えたこと

解法(1)：累積和

コード

解法(2)：DP に付加状態を持たせる

コード