AOJ 3176 Plane Graph (HUPC 2020 day3-E)

原案でした！僕は比較的アドホック寄りの問題を作る傾向があったかもだけど、これは典型な感じ。

問題へのリンク

問題概要

頂点数 、辺数 の連結な平面グラフが与えられます。ここで、各頂点の座標 も入力として与えられます。

どの 3 点も一直線上にはありません。また、橋も関節点もありません。したがって、平面グラフは多角形を敷き詰めたものとみなすことができます。これらの多角形のうち、内部に頂点や辺を含まないものの面積の最大値を 2 倍した値を求めてください。

制約

• 
• 

考えたこと

多角形をすべて抽出しよう！！！
各頂点 v ごとに、あらかじめ、v に接続する辺を偏角でソートしておくことにする。 そして、平面グラフの各辺に対応して、双方向の向きの辺をつけた有向グラフとして考えることにする。

そして目的はこういう風にすること。

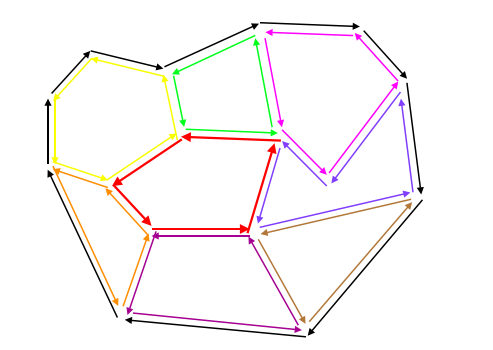
以下を貪欲に繰り返すことで、面をすべて抽出できる。

• 有向辺 (u, v) が残っているならば、それを一つ選ぶ
• v に接続している有向辺 (残っているもの) のうち、u の方向から時計回りに回して最初に出てくるものを選んで進む
• 以後、終点が u になるまでこれを繰り返す
• そうすると、出来上がるものは以下のいずれかになるので、それを構成する有向辺をすべて削除する
  • 内部に点を一つも含まない多角形 (それを構成する有向辺は反時計回り)
  • 平面グラフの外側 (これだけそれを構成する有向辺が時計回り)

こうしてできた多角形の符号付き面積を求めていけば OK。

#include <bits/stdc++.h>
using namespace std;
template<class T> inline bool chmax(T& a, T b) { if (a < b) { a = b; return 1; } return 0; }
template<class T> inline bool chmin(T& a, T b) { if (a > b) { a = b; return 1; } return 0; }

using DD = double;
const DD INF = 1LL<<60;      // to be set appropriately
const DD EPS = 1e-10;        // to be set appropriately
const DD PI = acosl(-1.0);
DD torad(int deg) {return (DD)(deg) * PI / 180;}
DD todeg(DD ang) {return ang * 180 / PI;}

/* Point */
struct Point {
    DD x, y;
    Point(DD x = 0.0, DD y = 0.0) : x(x), y(y) {}
    friend ostream& operator << (ostream &s, const Point &p) {return s << '(' << p.x << ", " << p.y << ')';}
};
inline Point operator + (const Point &p, const Point &q) {return Point(p.x + q.x, p.y + q.y);}
inline Point operator - (const Point &p, const Point &q) {return Point(p.x - q.x, p.y - q.y);}
inline Point operator * (const Point &p, DD a) {return Point(p.x * a, p.y * a);}
inline Point operator * (DD a, const Point &p) {return Point(a * p.x, a * p.y);}
inline Point operator * (const Point &p, const Point &q) {return Point(p.x * q.x - p.y * q.y, p.x * q.y + p.y * q.x);}
inline Point operator / (const Point &p, DD a) {return Point(p.x / a, p.y / a);}
inline Point conj(const Point &p) {return Point(p.x, -p.y);}
inline Point rot(const Point &p, DD ang) {return Point(cos(ang) * p.x - sin(ang) * p.y, sin(ang) * p.x + cos(ang) * p.y);}
inline Point rot90(const Point &p) {return Point(-p.y, p.x);}
inline DD cross(const Point &p, const Point &q) {return p.x * q.y - p.y * q.x;}
inline DD dot(const Point &p, const Point &q) {return p.x * q.x + p.y * q.y;}
inline DD norm(const Point &p) {return dot(p, p);}
inline DD abs(const Point &p) {return sqrt(dot(p, p));}
inline DD amp(const Point &p) {DD res = atan2(p.y, p.x); if (res < 0) res += PI*2; return res;}
inline bool eq(const Point &p, const Point &q) {return abs(p - q) < EPS;}
inline bool operator < (const Point &p, const Point &q) {return (abs(p.x - q.x) > EPS ? p.x < q.x : p.y < q.y);}
inline bool operator > (const Point &p, const Point &q) {return (abs(p.x - q.x) > EPS ? p.x > q.x : p.y > q.y);}
inline Point operator / (const Point &p, const Point &q) {return p * conj(q) / norm(q);}

/* Line */
struct Line : vector<Point> {
    Line(Point a = Point(0.0, 0.0), Point b = Point(0.0, 0.0)) {
        this->push_back(a);
        this->push_back(b);
    }
    friend ostream& operator << (ostream &s, const Line &l) {return s << '{' << l[0] << ", " << l[1] << '}';}
};

DD CalcArea(const vector<Point> &pol) {
    DD res = 0.0;
    for (int i = 0; i < pol.size(); ++i) {
        res += cross(pol[i], pol[(i+1)%pol.size()]);
    }
    return res/2.0L;
}

int N, M;
vector<Point> allp;
vector<vector<int>> G;

DD ang(int from, int to) {
    Point p = allp[to] - allp[from];
    return amp(p);
}

long long solve() {
    long long res = 0;
    vector<map<int,int>> next(N);
    vector<map<int,bool>> used(N);
    for (int v = 0; v < N; ++v) {
        vector<int> edges = G[v];
        sort(edges.begin(), edges.end(), [&](int a, int b) {
            return ang(v, a) < ang(v, b);
        });
        for (int j = 0; j < edges.size(); ++j) {
            next[v][edges[j]] = edges[(j+1)%edges.size()];
            used[v][edges[j]] = false;
        }
    }
    for (int v = 0; v < N; ++v) {
        for (int i = 0; i < G[v].size(); ++i) {
            int to = G[v][i];
            if (used[v][to]) continue;
  
            vector<Point> vp;
            int cur = v;
            do {
                vp.push_back(allp[cur]);
                used[cur][to] = true;
                int nto = next[to][cur];
                cur = to;
                to = nto;
            } while (cur != v);
            DD area = CalcArea(vp);
            if (area < 0) {
                area = -area * 2;
                long long tmp = (long long)(area + 0.1);
                chmax(res, tmp);
            }
        }
    }
    return res;
}

int main() {
    cin >> N >> M;
    allp.resize(N);
    for (int i = 0; i < N; ++i) cin >> allp[i].x >> allp[i].y;
    G.assign(N, vector<int>());
    for (int i = 0; i < M; ++i) {
        int u, v;
        cin >> u >> v;
        --u, --v;
        G[u].push_back(v);
        G[v].push_back(u);
    }
    cout << solve() << endl;
}