時は 2020 年 5 月 3 日。
ここ最近、AtCoder では、「再帰関数を用いた DFS な全探索」というタイプの問題が激増しています！！！

これらの多くは緑後半から水色前半の difficulty を叩き出す、とても恐れられている問題たちです。しかし実のところ、「ちょっと複雑だけど、単純に全探索するだけ」という側面もあります。

これらの出題が最近急増しているのは、おそらくは AtCoder 社側に

最近の AtCoder 参加者は数学パズル的な問題を解きすぎていて、こういうむしろプログラミングに寄った全探索ができない傾向にある
そういう出題を増やすことで、そういうのに慣れてもらいたい

という危機感があるのだと思われます。こういう「複雑だけど全探索するだけ」という雰囲気の問題は、大昔の競プロではむしろ主流でした。数学要素が強めな出題傾向は、割と最近のことのようです。

全体レベルがドンドン上がっていると言われている中、こうした古き良き雰囲気の問題は、むしろ difficulty が高く出てしまう傾向にあります。よって、逆に言えば

「複雑だけど全探索するだけ」という問題は、プログラミング力を問う側面が強く、数学経験値の大小に左右されない！！！
練習すればするだけ解けるようになるし、慣れれば発想は不要なので簡単！！
よって差をつけられる！！

ということで、慣れればお買い得な問題と言えます！！！

1. 再帰関数のモチベーション

再帰関数って、一口にいっても、色んな使い方があります！

しかしここでは、下に挙げたような「あまりにもエグい多重 for 文」を再帰関数にする、という使い方を徹底的に練習していきたいと思います！それができれば、上に挙げた、最近の AtCoder の DFS 全探索問題が大体解けます！！！

#include <bits/stdc++.h>
using namespace std;

int main() {
    const int M = 2;
    for (int a = 0; a < M; ++a) {
        for (int b = 0; b < M; ++b) {
            for (int c = 0; c < M; ++c) {
                for (int d = 0; d < M; ++d) {
                    for (int e = 0; e < M; ++e) {
                        for (int f = 0; f < M; ++f) {
                            for (int g = 0; g < M; ++g) {
                                for (int h = 0; h < M; ++h) {
                                    for (int i = 0; i < M; ++i) {
                                        for (int j = 0; j < M; ++j) {
                                            cout << a << b << c << d << e << f << g << h << i << j << endl;
                                        }
                                    }
                                }
                            }
                        }
                    }
                }
            }
        }
    }
}

ちなみにこのエグい多重ブープは、 $2^{10} = 1024$ 通りの 0, 1 列を出力するコードになっています。出力結果は下のようになります。

こういうエグい多重ループは、大抵の場合、再帰関数で機械的に書き直すことができます！！！

具体的な再帰関数の書き方の詳細は後に回すとして、試しに下のコードを実行すると、全く同じ出力結果になるはずです！！！

#include <bits/stdc++.h>
using namespace std;

const int M = 2;
void dfs(vector<int> &A) {
    // 終端条件 --- 10 重ループまで回したら処理して打ち切り
    if (A.size() == 10) {
        for (int i = 0; i < 10; ++i) cout << A[i];
        cout << endl;
        return;
    }

    for (int v = 0; v < M; ++v) {
        A.push_back(v);
        dfs(A);
        A.pop_back(); // これが結構ポイント
    }
}

int main() {
    vector<int> A;
    dfs(A);
}

これは Python だと、下のように書けます (本当は itertools を使えばもっと簡単に書けたりもしますが、応用は効かない感じです)！

M = 2
def dfs(A):
    # 終端条件 --- 10 重ループまで回したら処理して打ち切り
    if len(A) == 10:
        print(A)
        return
    for v in range(M):
        A.append(v)
        dfs(A)
        A.pop() # これが結構ポイント

dfs([])

なお、このような出力結果を見て「これ bit 全探索もできるやん」と思った方も多いかもしれません。実際、bit 全探索を再帰関数で実現する上での注意点などを細かく解説した記事も以前書きました！！！

drken1215.hatenablog.com

さて、このような再帰関数の書き方は、実は、ほとんどテンプレ化することができます。そこで本記事では、

「テンプレ化された再帰関数」に慣れる

ことによって、様々な探索を実現できるようにしていきます！

2. 再帰関数の書き方

さて、多重 for 文が何をしているのかを思い起こしてみましょう。多重 for 文というのは結局、

ある条件を満たす「数列」を全探索する

というのをしていると言えます。上のエグい多重 for 文も、言い換えれば、

0 または 1 からなる、長さ 10 の数列 ( $2^{10} = 1024$ 通りある)

を全探索しています。ここで再帰関数の出番です！再帰関数を使うと、色んな数列を簡単に生成することができます！

このように数列を生成する再帰関数は、大体次のような実装テンプレで対応できます！！！ただし、ここでは

長さ $N$ の数列を生成したい
数列の各項の値は $0, 1, \dots, M-1$ であるようにしたい

という状況を考えています (そのような数列は $M^{N}$ 通りあります)。

C++ 版

void dfs(vector<int> &A) {
    // 数列の長さが N に達したら打ち切り
    if (A.size() == N) {
        // 処理
        return;
    }

    for (int v = 0; v < M; ++v) {
        A.push_back(v);
        dfs(A);
        A.pop_back();
    }
}

int main() {
    vector<int> A;
    dfs(A);
}

Python 版

def dfs(A):
    # 数列の長さが N に達したら打ち切り
    if len(A) == N:
        # 処理
        return
    for v in range(M):
        A.append(v)
        dfs(A)
        A.pop()

dfs([])

この再帰関数の挙動を図示すると、下図のようになります。

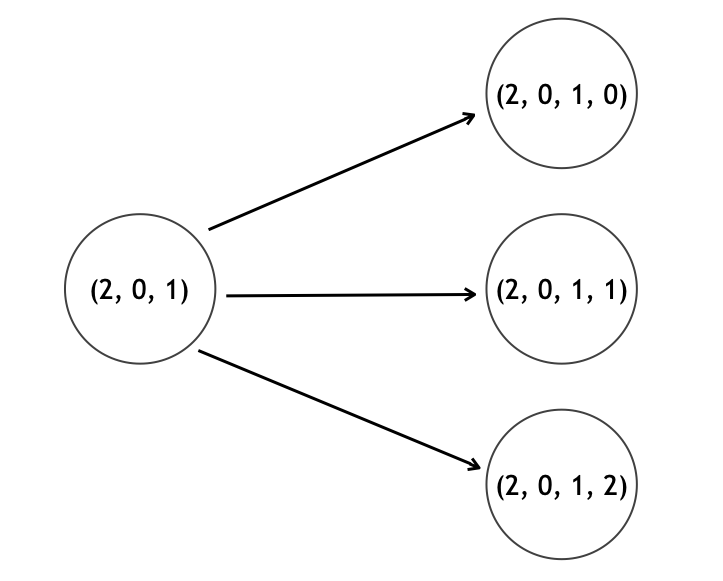
具体的に何をしているのかを順を追って見ていきましょう。たとえば $N = 5$ 、 $M = 3$ として、 $A = (2, 0, 1)$ の状態で dfs(A) が呼び出されるシチュエーションを考えてみます。このとき、

まず A の要素数が N (= 5) かどうかをチェックする → 違うのでスルー
最初に v = 0 について
- A に v を push (append) する → A = (2, 0, 1, 0) になる
- dfs(A) を再帰呼出しする
- A を pop する → A = (2, 0, 1) になる
次に v = 1 について
- A に v を push (append) する → A = (2, 0, 1, 1) になる
- dfs(A) を再帰呼出しする
- A を pop する → A = (2, 0, 1) になる
最後に v = 2 について
- A に v を push (append) する → A = (2, 0, 1, 2) になる
- dfs(A) を再帰呼出しする
- A を pop する → A = (2, 0, 1) になる

という流れになっています。つまり、下図のような分岐処理を行なっていることになります。

注意点として、for 文の中身は

A.push_back(v);  // v を push
dfs(A);  // 再帰呼出し
A.pop_back();  // pop

という三手一組になっていますが、最後の pop を忘れがちです。でもこれを実施しないと、下図のような分岐になってしまいます。

さて、この再帰関数 dfs を、一番最初に呼び出すときには、「空の配列」を引数に入れています。C++ では、

int main() {
    vector<int> A;
    dfs(A);
}

という風にしていて、Python では

dfs([])

という風にしています。そして、再帰呼出しが行われるたびに、要素が 1 つ 1 つ追加されていくことになります。最終的に配列の長さが $N$ になったら、処理が打ち切られます。

細かい注意点

上で紹介した、下のような「三手一組」の実装についてです。

for v in range(M):
     A.append(v)
     dfs(A)
     A.pop()

Python だと、次のようにしたくなるかもしれません。

for v in range(M):
    dfs(A + [v])

これでも正しく処理することができます。しかしながら、これだと、毎回リストを作り直すような挙動になるので、多少計算に時間がかかるようになります。

なお、今回の記事で扱っているような「数列生成」に限らず、このように

(次のノードへの遷移)
(再帰呼出し)
(一回元に戻す)

という三手一組の実装で動くアルゴリズムを、一般にバックトラックと呼ぶことがあります。ノード間の遷移を「差分」だけで実装しているので、一回一回コピーするよりも高速に動作します。

計算量

このような再帰関数の計算量を見積る方法を考えてみましょう。再帰関数では一般に、

分岐の回数 (つまり、下図の矢印の本数)

が、そのまま計算時間となります。本記事で扱うような再帰関数では、「異なるノードから同一のノードへの合流」がないため、

「分岐」 (下図の矢印) の本数
「ノード」 (下図の丸) の個数

は一致します (厳密には、ノード数は分岐数より 1 小さい)。よって、ありうるノードの個数を見積もれば、それがそのまま計算量となります！！！

たとえば、上のテンプレ再帰関数では、

各要素が $0, 1, \dots, M-1$ であるような
長さ $N$ の数列

を生成しました。このような数列は $M^{N}$ 通りあるので、計算量は $O(M^{N})$ となります。

3. 応用

上記のテンプレは、大抵の全探索 DFS を実現できてしまう程度には強いです！具体的な問題をいくつか解いてみましょう。

問題 1： AtCoder ABC 165 C - Many Requirements

$1 \le A_{1} \le A_{2} \le \dots \le A_{N} \le M$

という条件を満たす長さ $N$ の数列 $A_{1}, \dots, A_{N}$ を考える。そのうち、以下のようにして定まるスコアの最大値を求めよ。

スコアは、 $Q$ 個の条件のうち、満たすものについて加算されていく。

$i$ 個目の条件は、4 つの整数 $a_{i}, b_{i}, c_{i}, d_{i}$ で与えられる
数列 $A$ が、 $A_{b_{i}} - A_{a_{i}} = c_{i}$ を満たすならば、スコアに $d_{i}$ が加算される

制約

$N, M \le 10$
$Q \le 50$
$1 \le a_{i} \lt b_{i} \le M$

解法

条件を満たすような数列 $A$ を全探索することを考えてみましょう。 $A_{1}, \dots, A_{N}$ のとりうる値は $1, 2, \dots, M$ なので、上で示したテンプレにとてもよく似ています！！！！！

ただし、 $A_{1} \le A_{2} \le \dots \le A_{N}$ という条件を加味しなければなりません。でもこれは、次のコードのように、ちょっとした変更で実現することができます！！！

void dfs(vector<int> &A) {
    if (A.size() == N) {
        return;
    }

    int prev_last = (A.empty() ? 1 : A.back());
    for (int v = prev_last; v <= M; ++v) {
        A.push_back(v);
        dfs(A);
        A.pop_back();
    }
}

def dfs(A):
    if len(A) == N:
        print(A)
        return
    prev_last = A[-1] if len(A) > 0 else 1
    for v in range(prev_last, M+1):
        A.append(v)
        dfs(A)
        A.pop()

変わったのは for 文だけです。

v を $0$ から $M-1$ までの範囲で回す代わりに
v を (数列の前回の最後の値) から $M$ までの範囲で回す

という風に変更しています。このように、v を回す範囲を、「数列の前回の最後の値以上の範囲」に限ることで、「A が単調増加」という条件を上手に扱うことできています。

また注意点として、一番最初に関数 dfs を呼び出すときは、数列 A は空の状態です。このときだけは、A.back() (C++) や A[-1] (python) を呼び出してしまうと配列外参照になることに注意しましょう。

以上によって、条件を満たす数列 A を全て生成することができるので、それらに対してスコアを計算して、その最大値を出力すればよいです。

計算時間

なお、計算量が不安になるかもしれません。というのも、もし「数列 A が単調増加」という条件がなかったら、 $O(M^{N})$ となります。 $10^{10}$ は流石に間に合いません。

しかし、「単調増加」という条件によって、想像以上に選択肢が減ります。ものすごくざっくりとした感覚で言うと、

数列の長さが $2$ なら、選択肢の個数はざっくり $\frac{1}{2}$ になる
数列の長さが $3$ なら、選択肢の個数はざっくり $\frac{1}{6}$ になる
数列の長さが $4$ なら、選択肢の個数はざっくり $\frac{1}{24}$ になる
数列の長さが $5$ なら、選択肢の個数はざっくり $\frac{1}{120}$ になる
...
数列の長さが $N$ なら、選択肢の個数はざっくり $\frac{1}{N!}$ になる

というくらいに選択肢が減ります。今回は具体的には、92378 通りになります。ちゃんとした詳しい求め方はアルメリアさんの記事に書いてあります。

解答例 (C++)

ここでは、0-indexed で実装しました (数列の値範囲を 1〜M から 0〜M-1 とした)

また、今まで再帰関数 dfs の返り値は void 型で実装していたが、今回は、以下のように、「スコアの最大値」を返すようにしました。

dfs(A)：数列 A に要素を付け加えてできる数列すべてについてのスコアの最大値

少しわかりにくいかもしれません。たとえば $A = (1, 3)$ のときは、 $(1, 3, \dots)$ という形をした数列についてのスコアの最大値を求めることになります。これは具体的には、

$A = (1, 3, 3, \dots)$
$A = (1, 3, 4, \dots)$
$A = (1, 3, 5, \dots)$
...
$A = (1, 3, M-1, \dots)$

についての dfs(A) の値をすべて求めて、その最大値をとることで求められます。最終的には、空配列 A = () に対して dfs(A) の値が、求める最大値になります。

#include <bits/stdc++.h>
using namespace std;

// 入力
int N, M, Q;
vector<long long> a, b, c, d;

// 数列 A のスコアを計算
long long score(const vector<int> &A) {
    long long res = 0;
    for (int i = 0; i < Q; ++i) if (A[b[i]] - A[a[i]] == c[i]) res += d[i];
    return res;
}

// 数列 A に要素を付け加えて行って、最終的にできる数列のうちの
// スコアの最大値を返す
// 特に、最初の呼出しに対する返り値が答え
long long dfs(vector<int> &A) {
    if (A.size() == N) {
        return score(A);
    }
    long long res = 0;
    int prev_last = (A.empty() ? 0 : A.back());
    for (int add = prev_last; add < M; ++add) {
        A.push_back(add);
        res = max(res, dfs(A)); // 再帰呼出しながら、スコア最大値を更新
        A.pop_back();
    }
    return res;
}

int main() {
    cin >> N >> M >> Q;
    a.resize(Q); b.resize(Q); c.resize(Q); d.resize(Q);
    for (int q = 0; q < Q; ++q) {
        cin >> a[q] >> b[q] >> c[q] >> d[q];
        --a[q], --b[q];
    }
    vector<int> A;
    cout << dfs(A) << endl;
}

解答例 (Python)

Python なら、本当は itertools を使えば簡単に実現できます (maspyさんのコードなどを参照)。

しかしここでは C++ と同様の再帰関数で実装してみます。

# 入力
N, M, Q = map(int, input().split())
a = [0] * Q
b = [0] * Q
c = [0] * Q
d = [0] * Q
for i in range(Q):
    a[i], b[i], c[i], d[i] = map(int, input().split())
    a[i] -= 1
    b[i] -= 1

# スコア計算
def score(A):
    tmp = 0
    for ai, bi, ci, di in zip(a, b, c, d):
        if A[bi] - A[ai] == ci:
            tmp += di
    return tmp

# DFS
def dfs(A):
    if len(A) == N:
        return score(A) # 数列 A のスコアを返す
    res = 0
    prev_last = A[-1] if len(A) > 0 else 0
    for v in range(prev_last, M):
        A.append(v)
        res = max(res, dfs(A)) # 再帰呼出しながら、スコア最大値も更新
        A.pop()
    return res

# 求める
print(dfs([]))