けんちょんの競プロ精進記録

競プロの精進記録や小ネタを書いていきます

AtCoder Library Practice Contest G - SCC

AtCoder ACLpractice 強連結成分を考える 強連結成分分解 グラフ

まさに文字通り、強連結成分分解をしてください、という問題ですね。そしてこの問題は、Yosupo Judge の Strongly Connected Components が元になっているようです。

問題概要

N 頂点 M 辺の有向グラフが与えられる。

i 番目の辺は (a_{i}, b_{i}) である。このグラフは単純とは限らない。 ​ このグラフを強連結成分分解し、トポロジカルソートして出力してください。

制約

  • 1 \le N, M \le 5 \times 10^{5}

強連結成分分解 (SCC) とは

強連結成分分解 (Decomposition of Strongly Connected Components, SCC) とは、有向グラフにおいて 「お互いに行き来できる頂点を同じグループになるように頂点をグループ分けする」ことをいいます。    たとえば、次の有向グラフを見てみましょう。

  • 頂点 0, 2 は互いに行き来できます
    • 頂点 0 → 頂点 2：直接行けます
    • 頂点 2 → 頂点 0：頂点 3 を経由して行けます
  • 頂点 0, 4 は互いに行き来はできません
    • 頂点 0 から頂点 4 へは行けます
    • しかし、頂点 4 からは頂点 0 へ行けません

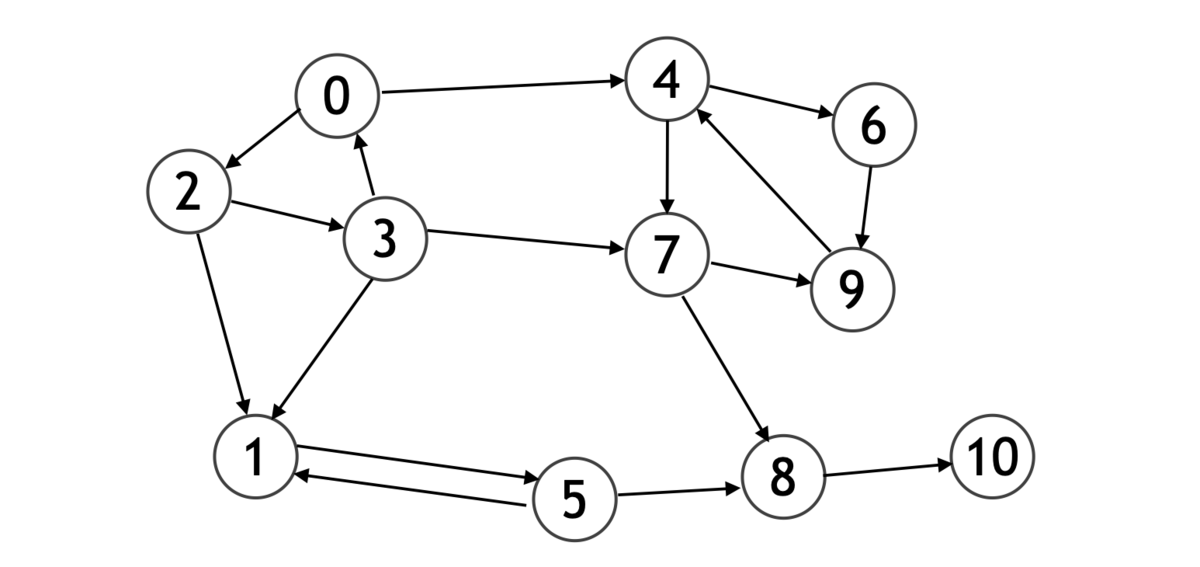
このグラフは、「互いに行き来できる関係」によってグループ分けすると、下図のようにグループ分けできます。

グループ A, B, C, D, E の内部の頂点たちは互いに行き来できます。しかし、異なるグループの頂点間は、一方から他方に行けることはあり得ますが、互いに行き来することはできません。

そして、各グループを新たな頂点とすることで、新たなグラフが作れます！　この新たなグラフでは、グループ間の辺を次のように張ります。

グループ P 内のある頂点から、グループ Q 内のある頂点に辺があるとき、グループ P からグループ Q へと辺を張ります。

このとき、仮にグループ P からグループ Q への辺が張られているときに、グループ Q からグループ P へと辺が張られることは絶対にあり得ないということに注意しましょう。なぜなら、もしそうなら、グループ P とグループ Q は自由に行き来できることとなり、本来は同じグループだということになってしまうためです。

ゆえに、新たに作られるグラフは DAG (Directed Acyclic Graph) となります。DAG とは「閉路のない有向グラフ」のことです。

　

ACL の強連結成分分解ライブラリ

さて、AtCoder の強連結成分分解ライブラリは、次のインターフェースになっています。

vector<vector<int>> graph.scc();

これは、次の条件を満たすような、「頂点のリスト」のリストを返します。

  • 各リストは強連結成分に対応します
  • 各リストは、強連結成分分解してできる DAG のトポロジカルソート順にソートされています

このライブラリは O(N+M) の計算量で動作します。アルゴリズムの詳細は、たとえば次の記事などを参照。

manabitimes.jp

また、ACL の SCC ライブラリの公式ドキュメントも参照:

https://atcoder.github.io/ac-library/production/document_ja/scc.html

　

AC コード

ACL の SCC ライブラリを使って AC しました。

#include <bits/stdc++.h>
#include <atcoder/scc>
using namespace std;
using namespace atcoder;

int main() {
    int N, M;
    cin >> N >> M;
    
    // SCC を適用するためのグラフを構築する
    scc_graph G(N);
    for (int i = 0; i < M; ++i) {
        int u, v;
        cin >> u >> v;
        G.add_edge(u, v);
    }
    
    // SCC
    auto scc = G.scc();
    
    // 出力
    cout << scc.size() << endl;
    for (auto list : scc) {
        cout << list.size();
        for (auto v : list) cout << " " << v;
        cout << endl;
    }
}

自前ライブラリでも AC

#include <bits/stdc++.h>
using namespace std;

struct SCC {
    using Edge = int;
    using SGraph = vector<vector<Edge>>;

    // input
    SGraph G, rG;

    // result
    vector<vector<int>> scc;
    vector<int> cmp;
    SGraph dag;

    // constructor
    SCC(int N) : G(N), rG(N) {}

    // add edge
    void addedge(int u, int v) {
        G[u].push_back(v);
        rG[v].push_back(u);
    }

    // decomp
    vector<bool> seen;
    vector<int> vs, rvs;
    void dfs(int v) {
        seen[v] = true;
        for (auto e : G[v]) if (!seen[e]) dfs(e);
        vs.push_back(v);
    }
    void rdfs(int v, int k) {
        seen[v] = true;
        cmp[v] = k;
        for (auto e : rG[v]) if (!seen[e]) rdfs(e, k);
        rvs.push_back(v);
    }

    // reconstruct
    set<pair<int,int>> newEdges;
    void reconstruct() {
        int N = (int)G.size();
        int dV = (int)scc.size();
        dag.assign(dV, vector<Edge>());
        newEdges.clear();
        for (int i = 0; i < N; ++i) {
            int u = cmp[i];
            for (auto e : G[i]) {
                int v = cmp[e];
                if (u == v) continue;
                if (!newEdges.count({u, v})) {
                    dag[u].push_back(v);
                    newEdges.insert({u, v});
                }
            }
        }
    }

    // main
    void solve() {
        // first dfs
        int N = (int)G.size();
        seen.assign(N, false);
        vs.clear();
        for (int v = 0; v < N; ++v) if (!seen[v]) dfs(v);

        // back dfs
        int k = 0;
        scc.clear();
        cmp.assign(N, -1);
        seen.assign(N, false);
        for (int i = N - 1; i >= 0; --i) {
            if (!seen[vs[i]]) {
                rvs.clear();
                rdfs(vs[i], k++);
                scc.push_back(rvs);
            }
        }

        // reconstruct
        reconstruct();
    }
};

int main() {
    int N, M;
    cin >> N >> M;
    
    // SCC を適用するためのグラフを構築する
    SCC scc(N);
    for (int i = 0; i < M; ++i) {
        int u, v;
        cin >> u >> v;
        scc.addedge(u, v);
    }
    scc.solve();
    
    // 出力
    cout << scc.scc.size() << endl;
    for (auto list : scc.scc) {
        cout << list.size();
        for (auto v : list) cout << " " << v;
        cout << endl;
    }
}