旧 ABC の C 問題の中でも、個人的に最難だと思う問題！
現代の ABC で出題されても水色 diff になると思う。

問題へのリンク

問題概要

英小文字のみからなる長さ $N$ の文字列 $S$ が与えられる。

$S$ の各文字を並べ替えてできる文字列 $T$ のうち、 $S_{i} \neq T_{i}$ となる $i$ が $K$ 個以下であるものを考える。

そのような文字列のうち、辞書順最小のものを求めよ。

制約

$0 \le K \le N \le 100$

考えたこと

「辞書順最小」と見たら、とにかく「先頭から順に、後先のことを考えず、極力小さい文字を持って来れないかを考える」という Greedy 解法が適用できる。

というわけなので、基本的には次のような疑似コードでこの問題が解けるはずである。なお、 $S_{i} \neq T_{i}$ となる $i$ の個数を「 $S$ と $T$ の距離」と呼ぶことにする。

string T = "";

// 先頭から順に 1 文字ずつ確定していく
for (int i = 0; i < N; ++i) {
    // まだ使える文字を小さい順に試す
    for (文字 c : まだ使える文字を小さい順に) {
        if (T の i 文字目を c にしたとき、T の残りを上手く並べれば S と T の距離を K 以下にできる) {
            T += c;
            break;
        }
    }
}

判定問題

上の疑似コードで、一つ大きな難関がある。

それは、 $T$ の $i$ 文字目を $c$ にしたとき、 $T$ の残りを上手く並べることで $S, T$ の距離を $K$ 以下にできるかどうかを判定することである。

整理すると、下図のように、

文字列 $S$ の末尾から $N-i-1$ 文字分に対して、
文字列 $S$ から、 $T$ の先頭から $i+1$ 文字に使用すると決めた文字を除外した文字たちを並び替えることで
末尾の $N-i-1$ 文字についての距離をある一定以下にできるかどうかを判定せよ

という問題になる。

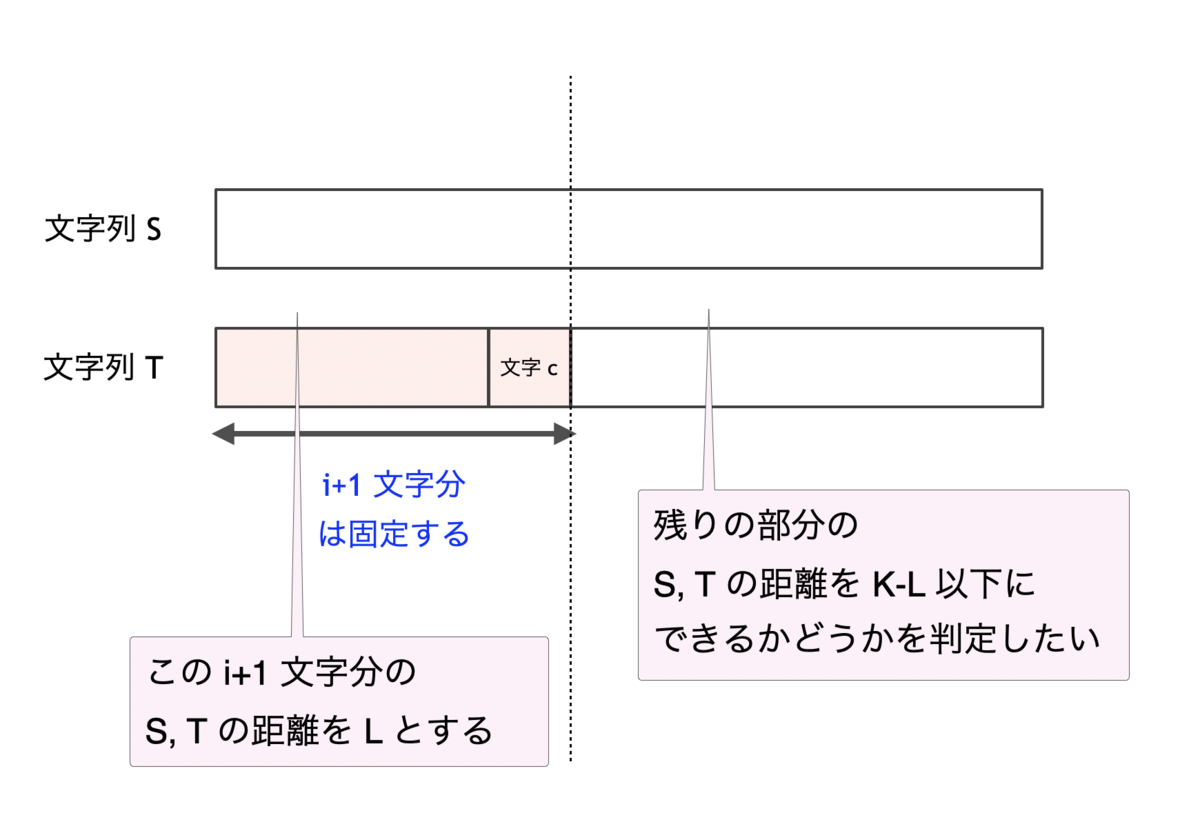
ここで、

文字列 $S$ の末尾から $N-i-1$ 文字分に含まれる文字 $c$ の個数を $s_{c}$ とする
文字列 $S$ から、 $T$ の先頭から $i+1$ 文字に使用すると決めた文字を除外して残る文字のうち、文字 $c$ の個数を $t_{c}$ とする

このとき、 $S_{i} = T_{i}$ となる $i$ を増やすためには

文字 'a' について、最大 $\min(s_{'a'}, t_{'a'})$ 個を一致させられる
文字 'b' について、最大 $\min(s_{'b'}, t_{'b'})$ 個を一致させられる
...
文字 'z' について、最大 $\min(s_{'z'}, t_{'z'})$ 個を一致させられる

というようになっている。これらは同時に実現できる。よって、末尾から $N-i-1$ 文字分についての最小コストは、

$N - i - 1 - \displaystyle \sum_{c = 'a'}^{'z'} \min(s_{'a'}, t_{'a'})$

と分かった。これが所望の値より小さければよい。

コード

以上のロジックを実装すればよい。 $N \le 100$ という制約から、計算量のことはあまり気にせず実装して大丈夫。

#include <bits/stdc++.h>
using namespace std;

int mincost(int n, map<char,int> Snum, map<char,int> Tnum) {
    int res = 0;
    for (char c = 'a'; c <= 'z'; ++c) res += min(Snum[c], Tnum[c]);
    return n - res;
}

int main() {
    int N, K;
    string S;
    cin >> N >> K >> S;
    
    map<char, int> Snum, Tnum;
    for (auto c : S) ++Snum[c], ++Tnum[c];
    
    string T = "";
    int L = 0;
    for (int i = 0; i < N; ++i) {
        --Snum[S[i]];
        for (auto [c, num] : Tnum) {
            if (num == 0) continue;
            --Tnum[c], L += (c != S[i]);
            if (mincost(N-i-1, Snum, Tnum) <= K - L) {
                T += c;
                break;
            }
            ++Tnum[c], L -= (c != S[i]);
        }
    }
    cout << T << endl;
}

けんちょんの競プロ精進記録

競プロの精進記録や小ネタを書いていきます

AtCoder ABC 009 C - 辞書式順序ふたたび (試験管青色)

問題概要

制約

考えたこと

判定問題

コード