こどふぉにありそうな雰囲気の問題かな

問題概要

$H$ × $W$ のグリッドの各マスをちょうど一回ずつ訪れたい。ただし

スタートとゴールは異なるマスでよい
毎回の移動は、上下左右斜めの 8 方向への移動は禁止 (飛車の移動も角の移動も禁止)

を満たすものが存在するか判定し、存在するならばそのような経路を 1 つ出力せよ。

制約

テストケース数 <= 100
$1 \le H, W \le 20$

考えたこと

頑張って場合分けしたけど、もっといい探索方法とかあるかもしれない。まず $H \le W$ として一般性を失わない。 $H$ > $W$ だった場合には、縦横 swap して解を求めて、最後にまた swap して出力すればよい。

H = 2 のとき

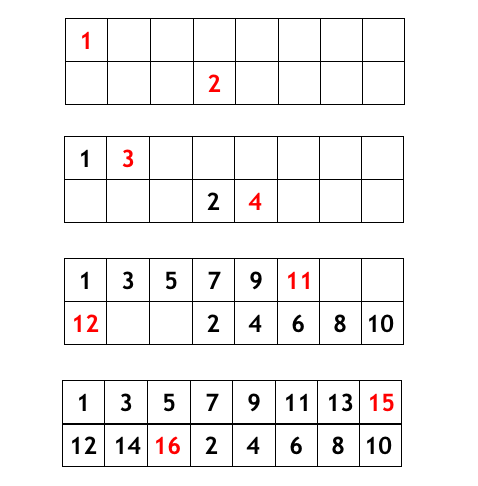
$W \le 4$ ではダメなことは書いてみればわかる。 $W \ge 5$ のときは下のように、

1 行目については順番に左から
2 行目については 1 行目から 3 マスずらして (右にはみ出すなら左に戻る)

順に埋めて行けばできる

H = 3 のとき

$W \le 3$ ではダメなことは書いてみればわかるし、そもそも $H = W = 3$ のときはマス $(2, 2)$ とつながっているマスがない。

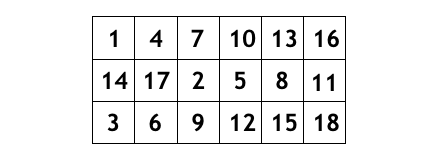
$W \ge 4$ のときは $H = 2$ のときと同様だが、

1 行目については順番に左から
2 行目については 1 行目から 2 マスずらして
3 行目については 1 行目と同じで

順に埋めていくことでできた。

H >= 4 のとき

$W \ge H$ を仮定していれば、必ずできる。基本的には

1 行目については順番に左から
2 行目については 1 行目から 2 マスずらして

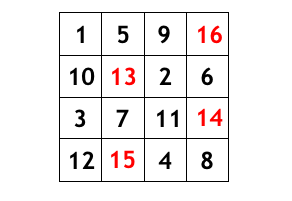
順に埋めていくことでできた。が、 $H = W$ かつ $H$ が偶数のときだけは例外で、最後だけ順序を入れ替えなければならなかった。例えば $H = W = 4$ のときはこんな感じ。16 のところに 13 を入れたいが、そうすると 12 と 13 がコンフリクトする。

#include <iostream>
#include <vector>
using namespace std;
using pint = pair<int,int>;

bool solve(int h, int w, vector<pint> &res) {
    if (h == 2) {
        if (w < 5) return false;
    }
    if (h == 3) {
        if (w < 4) return false;
    }
    if (h == 4) {
        if (w < 4) return false;
    }
    
    if (h == 2) {
        for (int j = 0; j < w; ++j) {
            for (int i = 0; i < h; ++i) {
                if (i % 2 == 0) res.push_back(pint(i, j));
                else res.push_back(pint(i, (j+3)%w));
            }
        }
        return true;
    }
    
    for (int j = 0; j < w; ++j) {
        for (int i = 0; i < h; ++i) {
            if (i % 2 == 0) res.push_back(pint(i, j));
            else res.push_back(pint(i, (j+2)%w));
        }
    }
    if (h % 2 == 0 && h == w) {
        auto p = res[h*w - h];
        res.erase(res.begin() + (h*w-h));
        res.push_back(p);
    }
    
    return true;
}

void solve() {
    int h, w; cin >> h >> w;
    bool swapped = false;
    if (h > w) swap(h, w), swapped = true;
    
    vector<pint> res;
    if (solve(h, w, res)) {
        cout << "POSSIBLE" << endl;
        for (auto p : res) {
            if (swapped) swap(p.first, p.second);
            cout << p.first + 1 << " " << p.second + 1 << endl;
        }
    }
    else cout << "IMPOSSIBLE" << endl;
}

int main() {
    int T; cin >> T;
    for (int _ = 0; _ < T; ++_) {
        cout << "Case #" << _+1 << ": ";
        solve();
    }
}