「予め盤面をいじることができる」という設定の問題にはある程度の定石があるように思う！

問題概要

$H \times W$ の盤面が与えられ、左上から右下まで行きたい。'#' マスは壁を表し、'.' マスは通路を表す。

予め盤面に以下の操作を行うことができる。最小回数の操作を行うことで、左上から右下まで、最短経路で (右か下への移動のみで) 到達できるようにせよ。

長方形区域を選んで、その中の通路と壁を反転する

制約

$2 \le H, W \le 100$

考えたこと

こういう「スタートする前に予め盤面をいじっておくことができる」というタイプの問題には一定の定石があるのだ。そういうタイプの類題としては、以下のような問題たちがある！

drken1215.hatenablog.com

こういうタイプの問題では、

まずは経路を一つ固定してみる
その経路が条件を満たすようにするための最小操作回数を求めてみる
それがわかれば、元の問題の解き方も自然とわかってくる

という流れが典型的だと思う。今回は、経路を固定してみると、下図のように、

経路中の連続する壁はまとめて破壊できる
経路中の飛び飛びの壁はまとめて破壊することはできない

ということがわかる。

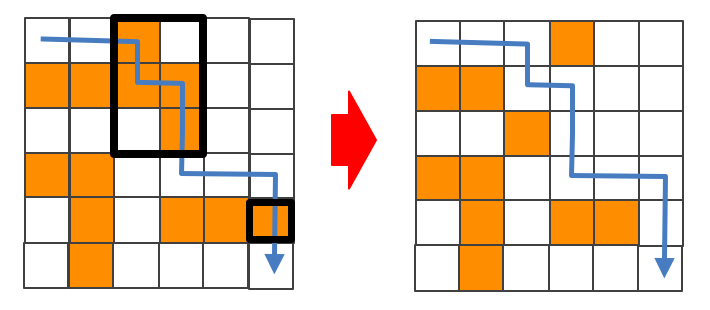
したがって元の問題は次のように言い換えることができるのだ。

以下のように左上から右下へ進みたい。その際に魔法を唱える回数をできるだけ減らしたい。魔法を唱える回数の最小値を求めよ。

魔法を唱えると壁の中に進むことができる
魔法が効いている間は壁の中をそのまま突き進むことができる
壁を抜けて通路に出ると、魔法の効果が切れる

(右か下にしか進めない)

ここまでわかれば、次のような DP を組むことができる。

dp[ x ][ y ] := マス (x, y) に到達するまでに魔法を唱える回数の最小値

初期値は

スタート地点が壁のとき： dp[ 0 ][ 0 ] = 1
スタート地点が通路のとき： dp[ 0 ][ 0 ] = 0

ということになる。そして、(x, y) から (nx, ny) への移動に関する DP 遷移は、

(nx, ny) が通路のとき： chmin(dp[ nx ][ ny ], dp[ x ][ y ])
(nx, ny) か壁で、(x, y) が通路のとき： chmin(dp[ nx ][ ny ], dp[ x ][ y ] + 1)
(nx, ny) が壁で、(x, y) も壁のとき： chmin(dp[ nx ][ ny ], dp[ x ][ y ])　(魔力が継続中)

として実現できる ( (nx, ny) = (x + 1, y) or (x, y + 1) )。

#include <bits/stdc++.h>
using namespace std;
template<class T> inline bool chmax(T& a, T b) { if (a < b) { a = b; return 1; } return 0; }
template<class T> inline bool chmin(T& a, T b) { if (a > b) { a = b; return 1; } return 0; }

const vector<int> dx = {1, 0};
const vector<int> dy = {0, 1};
const long long INF = 1LL<<60;
int H, W;
vector<string> fi;

long long solve() {
    vector<vector<long long>> dp(H, vector<long long>(W, INF));
    if (fi[0][0] == '#') dp[0][0] = 1;
    else dp[0][0] = 0;

    for (int i = 0; i < H; ++i) {
        for (int j = 0; j < W; ++j) {
            for (int dir = 0; dir < 2; ++dir) {
                int ni = i + dx[dir], nj = j + dy[dir];
                if (ni >= H || nj >= W) continue;
                int add = 0;
                if (fi[ni][nj] == '#' && fi[i][j] == '.') add = 1;
                chmin(dp[ni][nj], dp[i][j] + add);
            }
        }
    }
    return dp[H-1][W-1];
}

int main() {
    cin >> H >> W;
    fi.resize(H);
    for (int i = 0; i < H; ++i) cin >> fi[i];
    cout << solve() << endl;
}

けんちょんの競プロ精進記録

競プロの精進記録や小ネタを書いていきます

AtCoder AGC 043 A - Range Flip Find Route (緑色, 400 点)

問題概要

制約

考えたこと