問題概要

$N$ 人がいる。 $i$ 人目の人は、時刻 $S_{i}$ から時刻 $T_{i}$ の間で、毎分 $P_{i}$ リットルずつお湯を使う。

どの時刻においても、使用されているお湯の合計量が、毎分 $W$ リットル以内におさまるかどうかを判定せよ。

制約

$1 \le N \le 2 \times 10^{5}$
$0 \le S_{i} \lt T_{i} \le 2 \times 10^{5}$

考えたこと

大きさが $M = 2 \times 10^{5}$ の配列を考えて、初期状態は全マスの値が 0 としておく。

この配列に対して、 $N$ 個のクエリが飛んできて

マス $S_{i}, S_{i}+1, \dots, T_{i}-1$ の値を一様に $P_{i}$ だけ加算する

という処理をこなしていく。そして最後に、配列のすべてのマスの値が $W$ 以下になるかどうかを判定すればよい。

愚直にやると $O(N + MQ)$ の計算量を要してしまうので間に合わないが、いもす法を用いることで高速化できる！！

いもす法

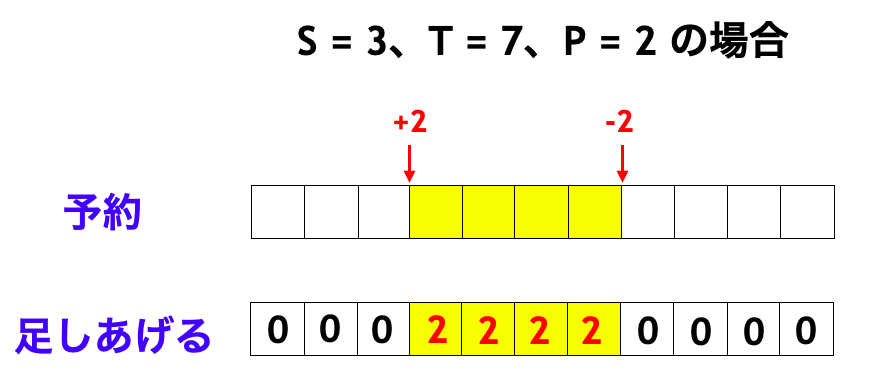
いもす法とは、 $N$ 個の区間を配列に足し上げた結果を高速に求める手法である。区間 $\lbrack S_{i}, T_{i})$ に値 $P_{i}$ を足すとは、下図のように

$S_{i}$ 番目の隙間に「+ $P_{i}$ 」という処理を予約しておく
$T_{i}$ 番目の隙間に「- $P_{i}$ 」という処理を予約しておく

という風にしておいて、最後に左から足しあげる (累積和をとる) ことで実現できる。

区間の個数が $N$ 個になっても同様にできる。 $N$ 個の区間それぞれに対して、「+ $P_{i}$ 」と「- $P_{i}$ 」をそれぞれ予約しておいて、最後にまとめて左から足しあげれば OK。このようにすると計算量は次のようになる。

予約パート：各区間に対して配列の 2 箇所にしか値を足し引きしないので、 $O(N)$
最後に足しあげるパート： $O(M)$

よって $O(N+M)$ でこの問題が解けることがわかった。

コード

#include <bits/stdc++.h>
using namespace std;

const int MAX = 210000;
int main() {
    long long N, W;
    cin >> N >> W;
    auto solve = [&]() {
        vector<long long> num(MAX+1, 0);
        for (int i = 0; i < N; ++i) {
            long long s, t, w;
            cin >> s >> t >> w;
            num[s] += w, num[t] -= w;
        }
        for (int v = 0; v < MAX; ++v) {
            num[v+1] += num[v];
            if (num[v] > W) return false;
        }
        return true;

    };
    cout << (solve() ? "Yes" : "No") << endl;
}