D 問題の MaxFlow に続いて、これまた、人生で一度は解くべき超典型問題ですね。そして、D 問題とは違うやり方で、二部グラフを作ることにも注目です！

問題へのリンク

問題概要

$N \times N$ のグリッドがあり、各マスには数値が書かれています。

これらのマスからいくつか選び、選んだ数値の総和が最大となるようにしてください。ただし、

どの行についても、その行に含まれる選んだマスの個数が $K$ 個以下
どの列についても、その列に含まれる選んだマスの個数が $K$ 個以下

となるようにします。また、総和が最大となる選び方を具体的に 1 つ示してください。

制約

$1 \le K \le N \le 50$
$0 \le A_{i, j} \le 10^{9}$

解法

「グリッドを見たら二部グラフを作る」という典型テクニックを使います。ただし、グリッドから二部グラフを作る方法としては、全く異なる 2 通りのものがあります。

行番号を左側ノード、列番号を右側ノードとした二部グラフ (今回)
グリッドを市松模様に塗り、黒色マスを左側ノード、白色マスを右側ノードとした二部グラフ (D 問題など)

今回は、1 の方法で二部グラフを作ります。下図のように、左側に行番号、右側に列番号を並べます。行 $i$ に対応する頂点と列 $j$ に対応する頂点とを結ぶ辺には、重さ $A_{i, j}$ を付します。

このとき、求める問題は「どの頂点についても、選ばれた辺の接続本数が $K$ 本以下となるように辺を選び、選んだ辺の重みを最大にする問題」となります。

なお、 $K = 1$ であれば、いわゆる最大重み二部マッチング問題ということになります。今回は、同じ頂点に $K$ 本までは接続が許されるので、マッチングを拡張したものと言えるでしょう。

最小費用流問題に帰着する

最大重み二部マッチング問題 ( $K = 1$ の場合) が最小費用流問題へと帰着できることはよく知られています。詳しくは次の記事を読んでみてください。また、最小費用流問題とは何かを知らない方も、この記事を読んでみてください。

qiita.com

今回も同様に、最小費用流問題へと帰着することができます。超頂点 $S, T$ を用意します。

そして、次のように辺を張って、フローネットワークを作ると良さそうです (実際はダメです)。問題の制約に対応するところは赤色にしています。

行 $i$ に対応する左側頂点から列 $j$ に対応する右側頂点へは、容量 $1$ 、コスト $-A_{i, j}$ の辺
$S$ から左側頂点へは、容量 $K$ 、コスト $0$ の辺
右側頂点から $T$ へは、容量 $K$ 、コスト $0$ の辺

最初のところで、コストを $-A_{i, j}$ というように、マイナスをつけているのは、「最大化問題」を「最小化問題」に変換するためです。

さて、こうして作ったフローネットワーク上で最小費用流を求めればよさそうです。しかし、最小費用流を流すときには、通常、流量を指定します。一見すると、流量 $NK$ の最小費用流を求めればいいように思われるかもしれません。しかし、入力例 2 にあるように、あえて選ぶマス数が $NK$ 個未満になるようにした方が最適になる場合があるのです！

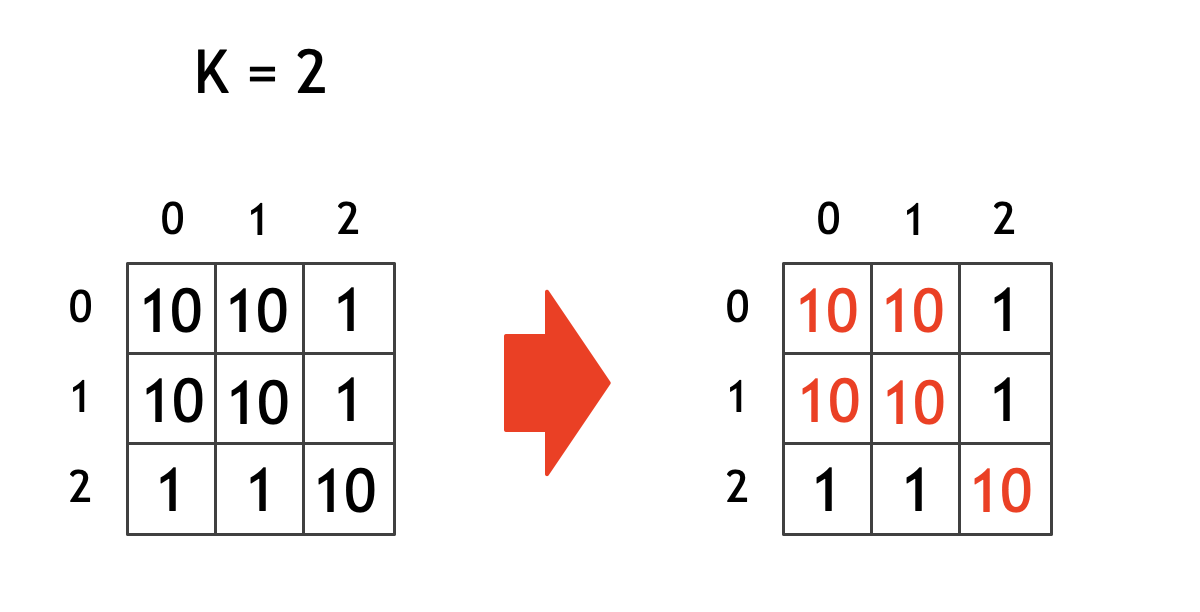
下図が実際の例です。各行各列ともに $K = 2$ 個まで選ぶことができるのですが、行 2 と列 2 については、1 個選ぶような方法が最適となっているのです。

工夫 1： $S$ から $T$ へとバイパスを作る

このような場合に対処する定石があります。それは、次のようなバイパス辺を新たに張ることです。

行 $i$ に対応する左側頂点から列 $j$ に対応する右側頂点へは、容量 $1$ 、コスト $-A_{i, j}$ の辺
$S$ から左側頂点へは、容量 $K$ 、コスト $0$ の辺
右側頂点から $T$ へは、容量 $K$ 、コスト $0$ の辺
頂点 $S$ から頂点 $T$ へ、容量 $\infty$ 、コスト $0$ の辺を張る

このグラフで改めて、流量 $NK$ の最小費用流を流せばよいでしょう。余分なフローはバイパスに流れてくれます。

工夫 2：負値をなくす

しかし、まだ問題があります。ACL のドキュメントによると、追加する辺のコストは負値であってはいけないようです。

そこで、二部グラフの左右を結ぶ辺とバイパス辺に対して、一律に十分大きい定数値 $B$ を足すことで、コストが負値になるようにします。このとき、流量 $NK$ のフローを流せば、フローのコスト値は一律に $BNK$ だけ増加することに注意します。

最終的に、最小費用流の値が res であったとき、選んだ数値の総和の最大値は B * N * K - res によって求められます。

最終形

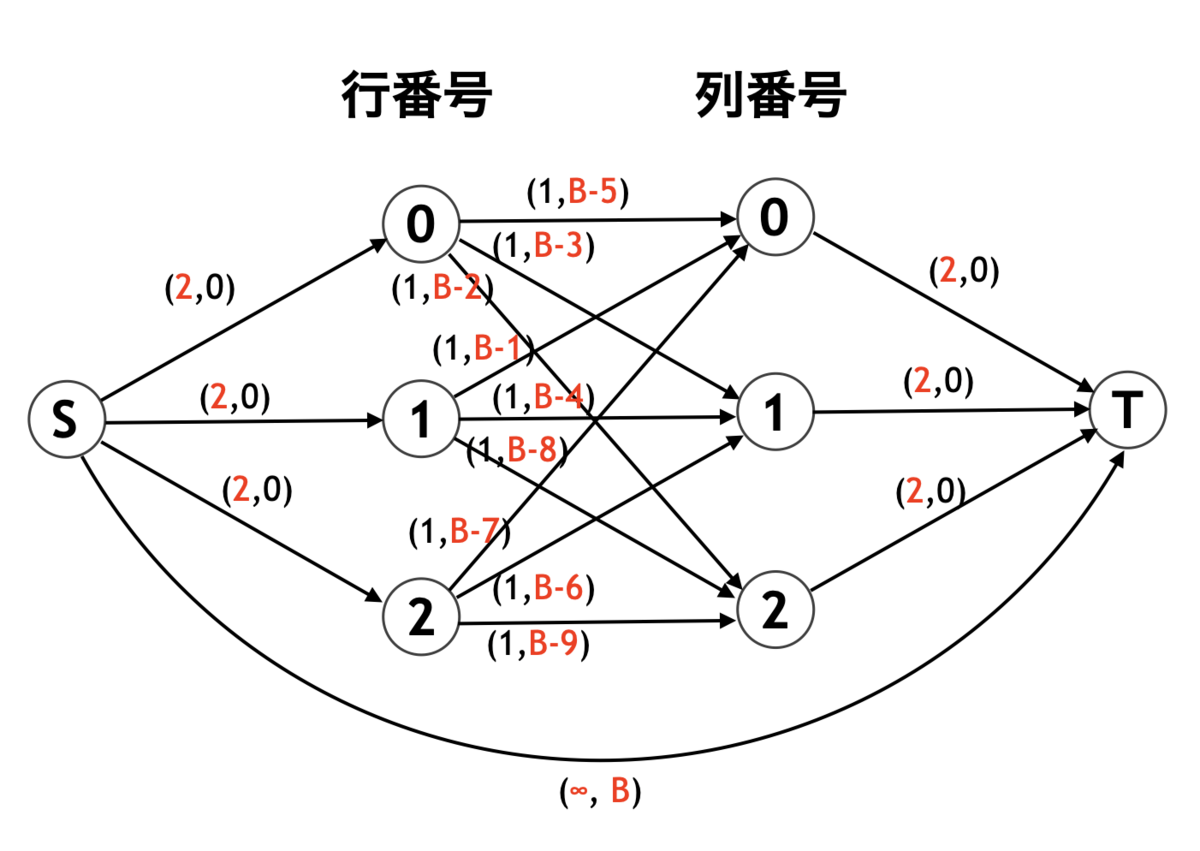
次のネットワークを作り、流量 $NK$ の最小費用流を求めます。

行 $i$ に対応する左側頂点から列 $j$ に対応する右側頂点へは、容量 $1$ 、コスト $B -A_{i, j}$ の辺
$S$ から左側頂点へは、容量 $K$ 、コスト $0$ の辺
右側頂点から $T$ へは、容量 $K$ 、コスト $0$ の辺
頂点 $S$ から頂点 $T$ へ、容量 $\infty$ 、コスト $B$ の辺を張る

コード

最小費用流問題を解くアルゴリズムについては、解説を他資料や他記事に譲ります。たとえば、蟻本に解説があります。

ここでは、ACL の提供している最小費用流アルゴリズムを活用します。ACL の提供するネットワークフロークラス mcf_graph<Cap, Cost> (Cap は容量や流量を表す型、Cost はコストを表す型) には、次のメソッドが用意されています。

int add_edge(int from, int to, Cap cap, Cost cost)：頂点 from から頂点 to へ、容量 cap、コスト cost の辺を張る (返り値は辺番号)
pair<Cap, Cost> graph.flow(int s, int t, Cap flow_limit)：頂点 s から頂点 t へ、流量が flow_limit を超えない範囲で、流せるだけ流す (返り値は {流せた流量, 最小費用流値})
vector<mf_graph<Cap, Cost>::edge> graph.edges()：辺集合を返す

なお、各辺を表す型 mf_graph::edge は、次のようになっています。

struct edge<Cap, Cost> {
    int from, to;
    Cap cap, flow;
    Cost cost;
};

これらの仕様を元にして、グラフネットワークを構築して、最小費用流を流し、フローの流れた辺を特定して、選ぶマスを復元しましょう。

次のように実装できます。

ACL を用いた実装

#include <bits/stdc++.h>
#include <atcoder/mincostflow>
using namespace std;
using namespace atcoder;

void ACL_practice_E() {
    // 十分大きな値
    const long long B = 1LL<<40;
    
    // 入力
    int N, K;
    cin >> N >> K;
    vector<vector<long long>> A(N, vector<long long>(N));
    for (int i = 0; i < N; ++i) for (int j = 0; j < N; ++j) cin >> A[i][j];
    
    // フローネットワークを作る
    // 行番号に対応する頂点を 0, 1, ..., N-1、列番号に対応する頂点を N, N+1, ..., 2N-1 とする
    // 超頂点の番号を S = 2N, T = 2N+1 とする
    mcf_graph<int, long long> G(N * 2 + 2);
    int S = N * 2, T = N * 2 + 1;
    
    // 行と列を結ぶ
    for (int i = 0; i < N; ++i) {
        for (int j = 0; j < N; ++j) {
            // 容量 1、コスト B - A[i][j]
            G.add_edge(i, j + N, 1, B - A[i][j]);
        }
    }
    
    // 超頂点
    for (int i = 0; i < N; ++i) {
        G.add_edge(S, i, K, 0);  // 容量 K, コスト 0
        G.add_edge(i + N, T, K, 0);  // 容量 K, コスト 0
    }
    
    // バイパス
    G.add_edge(S, T, N * K, B);
    
    // 流量 N * K の最小費用流を流す (最大流量も受け取るが N * K になることは分かっている)
    auto [max_flow, min_cost] = G.flow(S, T, N * K);
    
    // 復元する
    vector<string> grid(N, string(N, '.'));
    const auto &edges = G.edges();
    for (const auto &e : edges) {
        // 超頂点が絡む辺や、フローの流れなかった辺はスキップ
        if (e.from == S || e.to == T || e.flow == 0) continue;
        
        // 行 e.from、列 e.to - N が選ばれる
        grid[e.from][e.to - N] = 'X';
    }
    
    // 出力
    cout << B * N * K - min_cost << endl;
    for (int i = 0; i < N; ++i) cout << grid[i] << endl;
}

int main() {
    ACL_practice_E();
}

自前ライブラリでも AC

自分用に整備した最小費用流ライブラリでも AC した。

#include <bits/stdc++.h>
using namespace std;

// edge class (for network-flow)
template<class FLOWTYPE, class COSTTYPE> struct FlowCostEdge {
    // core members
    int rev, from, to;
    FLOWTYPE cap, icap, flow;
    COSTTYPE cost;
    
    // constructor
    FlowCostEdge(int rev, int from, int to, FLOWTYPE cap, COSTTYPE cost)
    : rev(rev), from(from), to(to), cap(cap), icap(cap), flow(0), cost(cost) {}
    void reset() { cap = icap, flow = 0; }
    
    // debug
    friend ostream& operator << (ostream& s, const FlowCostEdge& e) {
        return s << e.from << " -> " << e.to
        << " (" << e.flow << "/" << e.icap << ", " << e.cost << ")";
    }
};

// graph class (for network-flow)
template<class FLOWTYPE, class COSTTYPE> struct FlowCostGraph {
    // core members
    vector<vector<FlowCostEdge<FLOWTYPE, COSTTYPE>>> list;
    vector<pair<int,int>> pos;  // pos[i] := {vertex, order of list[vertex]} of i-th edge
    
    // constructor
    FlowCostGraph(int n = 0) : list(n) { }
    void init(int n = 0) {
        list.assign(n, FlowCostEdge<FLOWTYPE, COSTTYPE>());
        pos.clear();
    }
    
    // getter
    vector<FlowCostEdge<FLOWTYPE, COSTTYPE>> &operator [] (int i) {
        return list[i];
    }
    const vector<FlowCostEdge<FLOWTYPE, COSTTYPE>> &operator [] (int i) const {
        return list[i];
    }
    size_t size() const {
        return list.size();
    }
    FlowCostEdge<FLOWTYPE, COSTTYPE> &get_rev_edge
    (const FlowCostEdge<FLOWTYPE, COSTTYPE> &e) {
        if (e.from != e.to) return list[e.to][e.rev];
        else return list[e.to][e.rev + 1];
    }
    FlowCostEdge<FLOWTYPE, COSTTYPE> &get_edge(int i) {
        return list[pos[i].first][pos[i].second];
    }
    const FlowCostEdge<FLOWTYPE, COSTTYPE> &get_edge(int i) const {
        return list[pos[i].first][pos[i].second];
    }
    vector<FlowCostEdge<FLOWTYPE, COSTTYPE>> get_edges() const {
        vector<FlowCostEdge<FLOWTYPE, COSTTYPE>> edges;
        for (int i = 0; i < (int)pos.size(); ++i) {
            edges.push_back(get_edge(i));
        }
        return edges;
    }
    
    // change edges
    void reset() {
        for (int i = 0; i < (int)list.size(); ++i) {
            for (FlowCostEdge<FLOWTYPE, COSTTYPE> &e : list[i]) e.reset();
        }
    }
    
    // add_edge
    void add_edge(int from, int to, FLOWTYPE cap, COSTTYPE cost) {
        pos.emplace_back(from, (int)list[from].size());
        list[from].push_back(FlowCostEdge<FLOWTYPE, COSTTYPE>
                             ((int)list[to].size(), from, to, cap, cost));
        list[to].push_back(FlowCostEdge<FLOWTYPE, COSTTYPE>
                           ((int)list[from].size() - 1, to, from, 0, -cost));
    }

    // debug
    friend ostream& operator << (ostream& s, const FlowCostGraph &G) {
        const auto &edges = G.get_edges();
        for (const auto &e : edges) s << e << endl;
        return s;
    }
};

// min-cost max-flow (<= limit_flow), slope ver.
template<class FLOWTYPE, class COSTTYPE> vector<pair<FLOWTYPE, COSTTYPE>>
MinCostFlowSlope(FlowCostGraph<FLOWTYPE, COSTTYPE> &G, int S, int T, FLOWTYPE limit_flow)
{
    // result values
    FLOWTYPE cur_flow = 0;
    COSTTYPE cur_cost = 0, pre_cost = -1;
    vector<pair<FLOWTYPE, COSTTYPE>> res;
    res.emplace_back(cur_flow, cur_cost);
    
    // intermediate values
    vector<COSTTYPE> dual((int)G.size(), 0), dist((int)G.size());
    vector<int> prevv((int)G.size(), -1), preve((int)G.size(), -1);
    
    // dual
    auto dual_step = [&]() -> bool {
        priority_queue<pair<COSTTYPE,int>, vector<pair<COSTTYPE,int>>, greater<pair<COSTTYPE,int>>> que;
        que.push({0, S});
        dist.assign((int)G.size(), numeric_limits<COSTTYPE>::max());
        dist[S] = 0;
        while (!que.empty()) {
            auto [cur_cost, v] = que.top();
            que.pop();
            if (dist[v] < cur_cost) continue;
            for (int i = 0; i < (int)G[v].size(); ++i) {
                const auto &e = G[v][i];
                COSTTYPE new_cost = e.cost + dual[v] - dual[e.to];
                if (e.cap > 0 && dist[e.to] > dist[v] + new_cost) {
                    dist[e.to] = dist[v] + new_cost;
                    prevv[e.to] = v;
                    preve[e.to] = i;
                    que.push({dist[e.to], e.to});
                }
            }
        }
        if (dist[T] == numeric_limits<COSTTYPE>::max()) return false;
        for (int v = 0; v < (int)G.size(); ++v) {
            if (dist[T] == numeric_limits<COSTTYPE>::max()) continue;
            dual[v] -= dist[T] - dist[v];
        }
        return true;
    };
    
    // primal
    auto primal_step = [&]() -> void {
        FLOWTYPE flow = limit_flow - cur_flow;
        COSTTYPE cost = -dual[S];
        for (int v = T; v != S; v = prevv[v]) {
            flow = min(flow, G[prevv[v]][preve[v]].cap);
        }
        for (int v = T; v != S; v = prevv[v]) {
            FlowCostEdge<FLOWTYPE, COSTTYPE> &e = G[prevv[v]][preve[v]];
            FlowCostEdge<FLOWTYPE, COSTTYPE> &re = G.get_rev_edge(e);
            e.cap -= flow, e.flow += flow;
            re.cap += flow, re.flow -= flow;
        }
        cur_flow += flow;
        cur_cost += flow * cost;
        if (pre_cost == cost) res.pop_back();
        res.emplace_back(cur_flow, cur_cost);
        pre_cost = cur_cost;
    };
    
    // primal-dual
    while (cur_flow < limit_flow) {
        if (!dual_step()) break;
        primal_step();
    }
    return res;
}

// min-cost max-flow, slope ver.
template<class FLOWTYPE, class COSTTYPE> vector<pair<FLOWTYPE, COSTTYPE>>
MinCostFlowSlope(FlowCostGraph<FLOWTYPE, COSTTYPE> &G, int S, int T)
{
    return MinCostFlowSlope(G, S, T, numeric_limits<FLOWTYPE>::max());
}

// min-cost max-flow (<= limit_flow)
template<class FLOWTYPE, class COSTTYPE> pair<FLOWTYPE, COSTTYPE>
MinCostFlow(FlowCostGraph<FLOWTYPE, COSTTYPE> &G, int S, int T, FLOWTYPE limit_flow)
{
    return MinCostFlowSlope(G, S, T, limit_flow).back();
}

// min-cost max-flow (<= limit_flow)
template<class FLOWTYPE, class COSTTYPE> pair<FLOWTYPE, COSTTYPE>
MinCostFlow(FlowCostGraph<FLOWTYPE, COSTTYPE> &G, int S, int T)
{
    return MinCostFlow(G, S, T, numeric_limits<FLOWTYPE>::max());
}


void ACL_practice_E() {
    // 十分大きな値
    const long long B = 1LL<<40;
    
    // 入力
    int N, K;
    cin >> N >> K;
    vector<vector<long long>> A(N, vector<long long>(N));
    for (int i = 0; i < N; ++i) for (int j = 0; j < N; ++j) cin >> A[i][j];
    
    // フローネットワークを作る
    // 行番号に対応する頂点を 0, 1, ..., N-1、列番号に対応する頂点を N, N+1, ..., 2N-1 とする
    // 超頂点の番号を S = 2N, T = 2N+1 とする
    FlowCostGraph<int, long long> G(N * 2 + 2);
    int S = N * 2, T = N * 2 + 1;
    
    // 行と列を結ぶ
    for (int i = 0; i < N; ++i) {
        for (int j = 0; j < N; ++j) {
            // 容量 1、コスト B - A[i][j]
            G.add_edge(i, j + N, 1, B - A[i][j]);
        }
    }
    
    // 超頂点
    for (int i = 0; i < N; ++i) {
        G.add_edge(S, i, K, 0);  // 容量 K, コスト 0
        G.add_edge(i + N, T, K, 0);  // 容量 K, コスト 0
    }
    
    // バイパス
    G.add_edge(S, T, N * K, B);
    
    // 流量 N * K の最小費用流を流す (最大流量も受け取るが N * K になることは分かっている)
    auto [max_flow, min_cost] = MinCostFlow(G, S, T, N * K);
    
    // 復元する
    vector<string> grid(N, string(N, '.'));
    const auto &edges = G.get_edges();
    for (const auto &e : edges) {
        // 超頂点が絡む辺や、フローの流れなかった辺はスキップ
        if (e.from == S || e.to == T || e.flow == 0) continue;
        
        // 行 e.from、列 e.to - N が選ばれる
        grid[e.from][e.to - N] = 'X';
    }
    
    // 出力
    cout << B * N * K - min_cost << endl;
    for (int i = 0; i < N; ++i) cout << grid[i] << endl;
}

int main() {
    ACL_practice_E();
}

けんちょんの競プロ精進記録

競プロの精進記録や小ネタを書いていきます

AtCoder Library Practice Contest E - MinCostFlow

問題概要

制約

解法

最小費用流問題に帰着する

工夫 1： $S$ から $T$ へとバイパスを作る

工夫 2：負値をなくす

最終形

コード

ACL を用いた実装

自前ライブラリでも AC

問題概要

制約

解法

最小費用流問題に帰着する

工夫 1： から へとバイパスを作る

工夫 2：負値をなくす

最終形

コード

ACL を用いた実装

自前ライブラリでも AC

工夫 1： $S$ から $T$ へとバイパスを作る