2024-03-31

AtCoder ABC 347 F - Non-overlapping Squares (黄色, 525 点)

AtCoder AtCoder525点 ABC-F 黄色diff 二次元グリッド二次元セグメント木セグメント木長方形を3枚並べるときの切れ目に着目するテク:reverse/rotateしてもう一回やる最適化問題最大スコア最大安定集合問題二次元累積和累積max DP 典型要素を詰め合わせた教育的問題差分更新累積和テク:左右両端からの累積和や累積結果を前処理コーナーケース鳩の巣原理

面白かった。JOI でもありそうな問題。長方形を 3 枚並べるのは典型らしい。

問題へのリンク

問題概要

$N \times N$ のグリッドがあって、各マス $(i, j)$ には数値 $A_{i, j}$ が描かれている。

このグリッド上で $M \times M$ の正方形を重ならないように 3 枚並べるとき、これらの正方形に覆われたマスの数値の最大値を求めよ。

制約

$2 \le N \le 1000$
$1 \le M \le \frac{N}{2}$
$0 \le A_{i, j} \le 10^{9}$

考えたこと：正方形の配置のパターン

2 枚の正方形を並べるとき、それらの正方形は

縦方向に切れ目のラインを入れることができる
横方向に切れ目のラインを入れることができる

のいずれかの条件を満たすことに着目しよう (両方を満たすこともある)。

このことから、3 枚の正方形を並べるとき、

縦に切れ目を引いて、「左に 2 枚」と「右の 1 枚」という配置にできる
縦に切れ目を引いて、「左に 1 枚」と「右の 2 枚」という配置にできる
横に切れ目を引いて、「上に 2 枚」と「下の 1 枚」という配置にできる
横に切れ目を引いて、「上に 1 枚」と「下の 2 枚」という配置にできる

という 4 つのパターンのいずれかを満たすことが分かる。さらに「左に 2 枚」なども「上下に 2 枚」と「左右に 2 枚」とに分かれる。このことも考慮すると、公式解説にあるように、結局、以下の 6 パターンを考慮すればよいことが分かる。

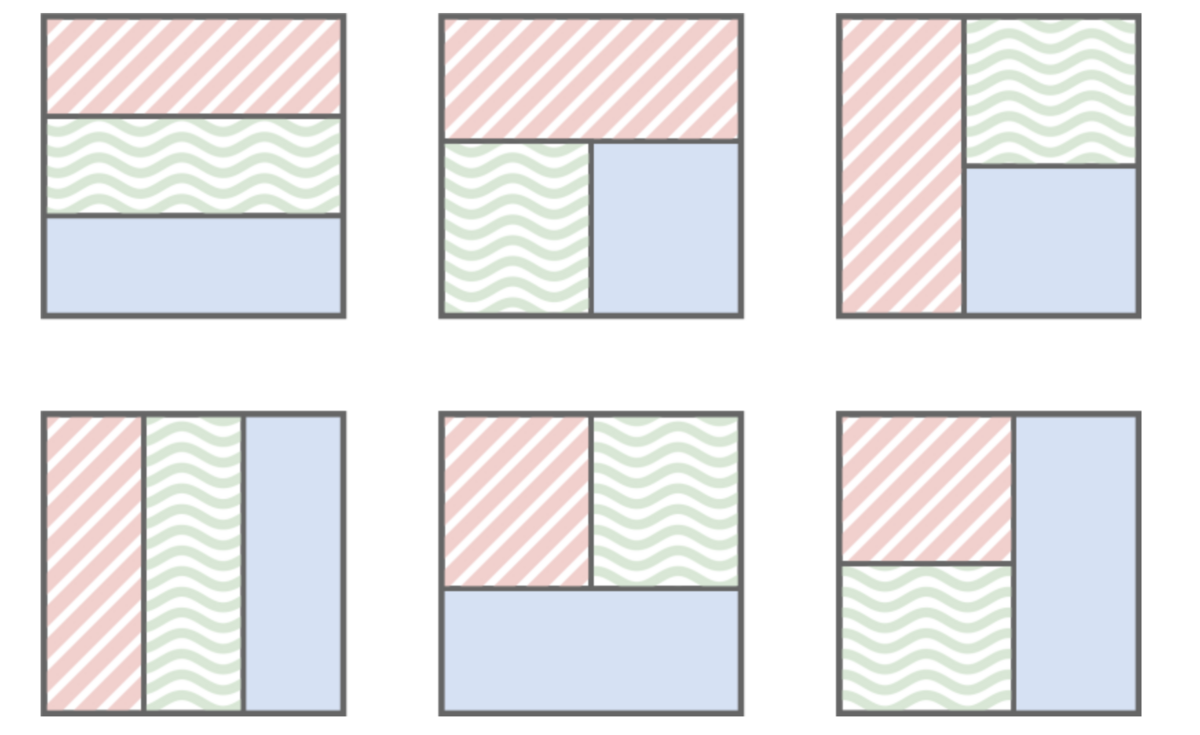
$h \times W$ に横に 2 枚並べる場合

ここまでパターン分解ができれば、あとは本質的には

$1 \times W$ , $2 \times W$ , $\dots$ の領域において、左右に 2 枚並べる場合の最適スコア

が求められればよいことがわかる (適切に盤面を回転するなどして)。ここでは次のような考え方で解いた。

$x \times W$ の長方形について考えるとき、各 $y = 0, 1, \dots, W-1$ について、左側の正方形の左辺が列 $y$ にある場合の最適スコアを求める。

これは、二次元セグメント木があれば、各 $(x, y)$ について $O(\log H + \log W)$ の計算量で求められる。

総じて、全体を通して $O(HW(\log H + \log W))$ の計算量で求められる。

コード

#include <bits/stdc++.h>
using namespace std;


// Segment Tree 2D
template<class Monoid> struct SegmentTree2D {
    using Func = function<Monoid(Monoid, Monoid)>;
    
    // core member
    int H, W;
    Func OP;
    Monoid IDENTITY;
    
    // inner data
    int log_H, offset_H, log_W, offset_W;
    vector<Monoid> dat;
    
    // constructor
    SegmentTree2D() {}
    SegmentTree2D(int h, int w, const Func &op, const Monoid &identity) {
        init(h, w, op, identity);
    }
    SegmentTree2D(const vector<vector<Monoid>> &v, const Func &op, const Monoid &identity) {
        init(v, op, identity);
    }
    void init(int h, int w, const Func &op, const Monoid &identity) {
        H = h, W = w;
        OP = op;
        IDENTITY = identity;
        log_H = 0, offset_H = 1, log_W = 0, offset_W = 1;
        while (offset_H < H) ++log_H, offset_H <<= 1;
        while (offset_W < W) ++log_W, offset_W <<= 1;
        dat.assign(offset_H * offset_W * 4, IDENTITY);
    }
    void init(const vector<vector<Monoid>> &v, const Func &op, const Monoid &identity) {
        init((int)v.size(), (int)v[0].size(), op, identity);
        build(v);
    }
    int id(int x, int y) const {
        return x * 2 * offset_W + y;
    }
    void build(const vector<vector<Monoid>> &v) {
        assert(H == (int)v.size()), assert(W == (int)v[0].size());
        for (int x = 0; x < H; ++x) {
            for (int y = 0; y < W; ++y) {
                dat[id(x + offset_H, y + offset_W)] = v[x][y];
            }
        }
        for (int y = offset_W; y < offset_W * 2; ++y) {
            for (int x = offset_H - 1; x; --x) {
                dat[id(x, y)] = OP(dat[id(x * 2, y)], dat[id(x * 2 + 1, y)]);
            }
        }
        for (int x = 0; x < offset_H * 2; ++x) {
            for (int y = offset_W - 1; y; --y) {
                dat[id(x, y)] = OP(dat[id(x, y * 2)], dat[id(x, y * 2 + 1)]);
            }
        }
    }
    Monoid operator () (int x, int y) const {
        return dat[id(x + offset_H, y + offset_W)];
    }
    
    // update
    void set(int x, int y, const Monoid &v) {
        assert(x >= 0 && x < H && y >= 0 && y < W);
        x += offset_H, y += offset_W;
        dat[id(x, y)] = v;
        for (int i = x >> 1; i; i >>= 1) {
            dat[id(i, y)] = OP(dat[id(i * 2, y)], dat[id(i * 2 + 1, y)]);
        }
        for (; x; x >>= 1) {
            for (int j = y >> 1; j; j >>= 1) {
                dat[id(x, j)] = OP(dat[id(x, j * 2)], dat[id(x, j * 2 + 1)]);
            }
        }
    }
    
    // prod
    Monoid inner_prod(int x, int yl, int yr) {
        Monoid res = IDENTITY;
        for (; yl < yr; yl >>= 1, yr >>= 1) {
            if (yl & 1) res = OP(res, dat[id(x, yl++)]);
            if (yr & 1) res = OP(dat[id(x, --yr)], res);
        }
        return res;
    }
    Monoid prod(int xl, int xr, int yl, int yr) {
        assert(0 <= xl && xl <= xr && xr <= H);
        assert(0 <= yl && yl <= yr && yr <= W);
        Monoid res = IDENTITY;
        xl += offset_H, xr += offset_H, yl += offset_W, yr += offset_W;
        for (; xl < xr; xl >>= 1, xr >>= 1) {
            if (xl & 1) res = OP(res, inner_prod(xl++, yl, yr));
            if (xr & 1) res = OP(inner_prod(--xr, yl, yr), res);
        }
        return res;
    }
    
    // debug
    friend ostream& operator << (ostream &s, const SegmentTree2D &seg) {
        for (int x = 0; x < seg.H; ++x) {
            for (int y = 0; y < seg.W; ++y) {
                s << seg(x, y) << " ";
            }
            s << endl;
        }
        return s;
    }
};



//------------------------------//
// Examples
//------------------------------//

// ABC 347 F - Non-overlapping Squares
void ABC_347_F() {
    const long long INF = 1LL<<55;
    long long res = 0;
    int N, M;
    cin >> N >> M;
    vector A(N, vector(N, 0LL)), S(N+1, vector(N+1, 0LL)), v(N-M+1, vector(N-M+1, -INF));
    for (int i = 0; i < N; ++i) {
        for (int j = 0; j < N; ++j) {
            cin >> A[i][j];
            S[i+1][j+1] = S[i+1][j] + S[i][j+1] - S[i][j] + A[i][j];
        }
    }
    for (int i = 0; i < N; ++i) {
        for (int j = 0; j < N; ++j) {
            if (i+M <= N && j+M <= N) {
                v[i][j] = S[i+M][j+M] - S[i+M][j] - S[i][j+M] + S[i][j];
            }
        }
    }
    auto v2 = v;
    int HW = (int)v.size();
    
    auto op = [](long long a, long long b) {return max(a, b);};
    {
        SegmentTree2D<long long> seg(v, op, -INF);
        for (int i = 0; i < HW; ++i) {
            for (int j = i+M; j+M < HW; ++j) {
                res = max(res, seg.prod(0, HW, i, i+1) + seg.prod(0, HW, j, j+1)
                          + seg.prod(0, HW, j+M, HW));
            }
        }
        for (int i = 0; i < HW; ++i) {
            for (int j = i+M; j+M < HW; ++j) {
                res = max(res, seg.prod(i, i+1, 0, HW) + seg.prod(j, j+1, 0, HW)
                          + seg.prod(j+M, HW, 0, HW));
            }
        }
    }

    auto calc = [&]() {
        SegmentTree2D<long long> seg(v, op, -INF);
        long long top = 0;
        for (int x = 1; x <= HW; ++x) {
            for (int y = 0; y+M < HW; ++y) {
                top = max(top, seg.prod(0, x, y, y+1) + seg.prod(0, x, y+M, HW));
            }
            if (x+M-1 < HW) res = max(res, top + seg.prod(x+M-1, HW, 0, HW));
        }
    };
    
    calc();
    reverse(v.begin(), v.end());
    calc();
    for (int i = 0; i < HW; ++i) for (int j = 0; j < HW; ++j) v[i][j] = v2[j][i];
    calc();
    reverse(v.begin(), v.end());
    calc();

    cout << res << endl;
}

int main() {
    ABC_347_F();
}