この時代多く見られた「グルーピング」の問題！

問題概要

S 型ピース 1 個と c 型ピース 2 個を使って、下図のように Scc を 1 個作ることができる。

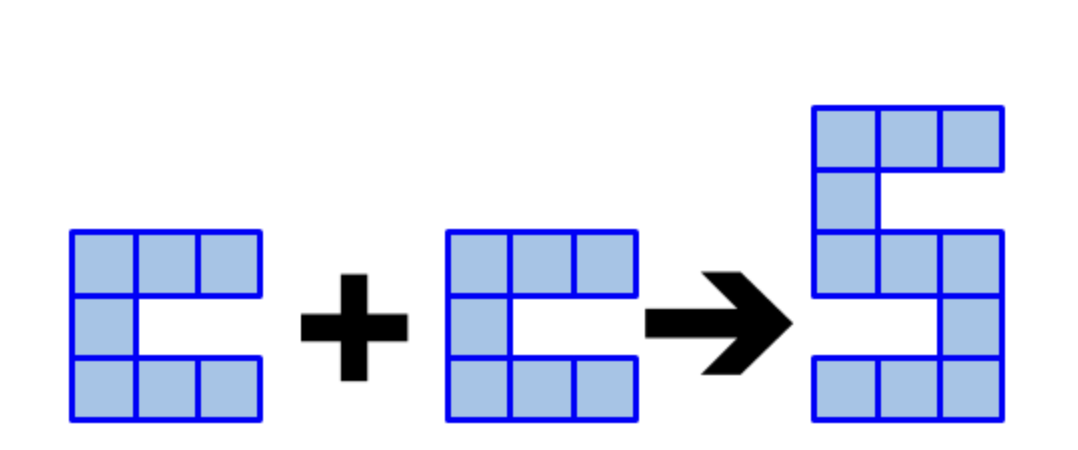
また、c 型ピース 2 個を使って S 型ピース 1 個を作ることもできる。

今、S 型ピースが $N$ 個、c 型ピースが $M$ 個ある。このとき、Scc を最大で何個作れるか？

制約

Scc を作るためには、S と c の両方が必要となる。よって、S が多すぎるときと、S が小さすぎるときとで状況が異なる。具体的には

というように区別できる。（が、最終的には閾値の考察は不要になる）

S を解体して c にすることはできない。よって、c の個数がネックとなる。c を限界まで使うと、Scc を

M / 2 個

作ることができる。

この場合は、c を組み合わせて S にすることができるので、c を目一杯使い切ることができる。よって、S や Scc も、c の個数に換算して考えればよい。次のように考えよう。

つまり、c が合計で $2N + M$ 個あると考えて良い。4 個の c で Scc を作れることから、求める Scc の個数は

(N * 2 + M) / 4 個

となる。

上記の 2 つの場合のうち、小さい方が答えだと考えられる。つまり、答えは

min(M / 2, (N * 2 + M) / 4) 個

である。

#include <bits/stdc++.h>
using namespace std;

int main() {
    long long N, M;
    cin >> N >> M;
    cout << min(M/2, (N*2+M)/4) << endl;
}