2024-12-29

AOJ 1458 Tree Generators (ICPC アジア 2024 D) (4D)

AOJ AOJ-ICPC ICPCアジア構文解析 stack 数え上げ問題数え上げ:積の法則各地点について自由度を掛け算していく考察：操作・条件・目的関数を言い換える構文解析木を構築するカッコ列操作操作:2つのものを1つにマージ

すごく悩んだけど、なんとか解けた！

問題へのリンク（仮）

問題概要

次の図のように、木を、文字 (、)、1 からなる文字列で表す（異なる木が同じ文字列になることもある）。文字列の生成規則は次のように表される。

E ::= ‘1’ | ‘(’ E E ‘)’

詳細は問題文を参照。

例：((1(11))1)

2 つの文字列 $S, T$ が与えられる。木であって、 $S$ からも $T$ からも生成され得るものの個数を 998244353 で割った余りを求めよ。

制約

$1 \le |S| = |T| \le 7 \times 10^{5}$

考えたこと

まずは、1 つの文字列から作られ得る木の個数を数えることにした。たとえば、Sample Input 3 の (((11)(11))((11)1)) を考える。これは 7 個の頂点からなる木である。上の文字列は、

頂点 1 からなる木と、頂点 2 からなる木が合体する（ここは 1 通り）
頂点 3 からなる木と、頂点 4 からなる木が合体する（ここは 1 通り）
頂点「1, 2」からなる木と、頂点「3, 4」からなる木が合体する（ここは 2 × 2 = 4 通り）
頂点 5 からなる木と、頂点 6 からなる木が合体する（ここは 1 通り）
頂点「5, 6」からなる木と、頂点 7 からなる木が合体する（ここは 2 × 1 = 2 通り）
頂点「1, 2, 3, 4」からなる木と、頂点「5, 6, 7」からなる木が合体する（ここは 4 × 3 = 12 通り）

と表せるので、木は全部で

1 × 1 × 4 × 1 × 2 × 12 = 96 通り

ある。

このような合体の過程は、「区間と区間の合体」ととらえることもできて、次のように再解釈できる。

区間 [1, 2) に含まれる頂点と、区間 [2, 3) に含まれる頂点を 1 つずつ選んで結ぶ（1 通り）
区間 [3, 4) に含まれる頂点と、区間 [4, 5) に含まれる頂点を 1 つずつ選んで結ぶ（1 通り）
区間 [1, 3) に含まれる頂点と、区間 [3, 5) に含まれる頂点を 1 つずつ選んで結ぶ（4 通り）
区間 [5, 6) に含まれる頂点と、区間 [6, 7) に含まれる頂点を 1 つずつ選んで結ぶ（1 通り）
区間 [5, 7) に含まれる頂点と、区間 [7, 8) に含まれる頂点を 1 つずつ選んで結ぶ（2 通り）
区間 [1, 5) に含まれる頂点と、区間 [5, 8) に含まれる頂点を 1 つずつ選んで結ぶ（12 通り）

さて、2 つの文字列 $S, T$ について、このように「区間と区間の合体」として捉えたときに、2 つの条件から生成される合体条件を混ぜこぜに考えるのは難しそうに思えた。何か分かりやすい特徴付けを見出そうと考えた。

まず、実は区間を合体する順序は関係ないのでは......と考えた。つまり、上の 6 回の辺を結ぶ順序は適当に入れ替えても良さそうだ。考えやすい順序として、合体する区間の境界（たとえば区間 [5, 7) と区間 [7, 8) の合体であれば、境界は 7）に着目すると、下図のように整理できる。

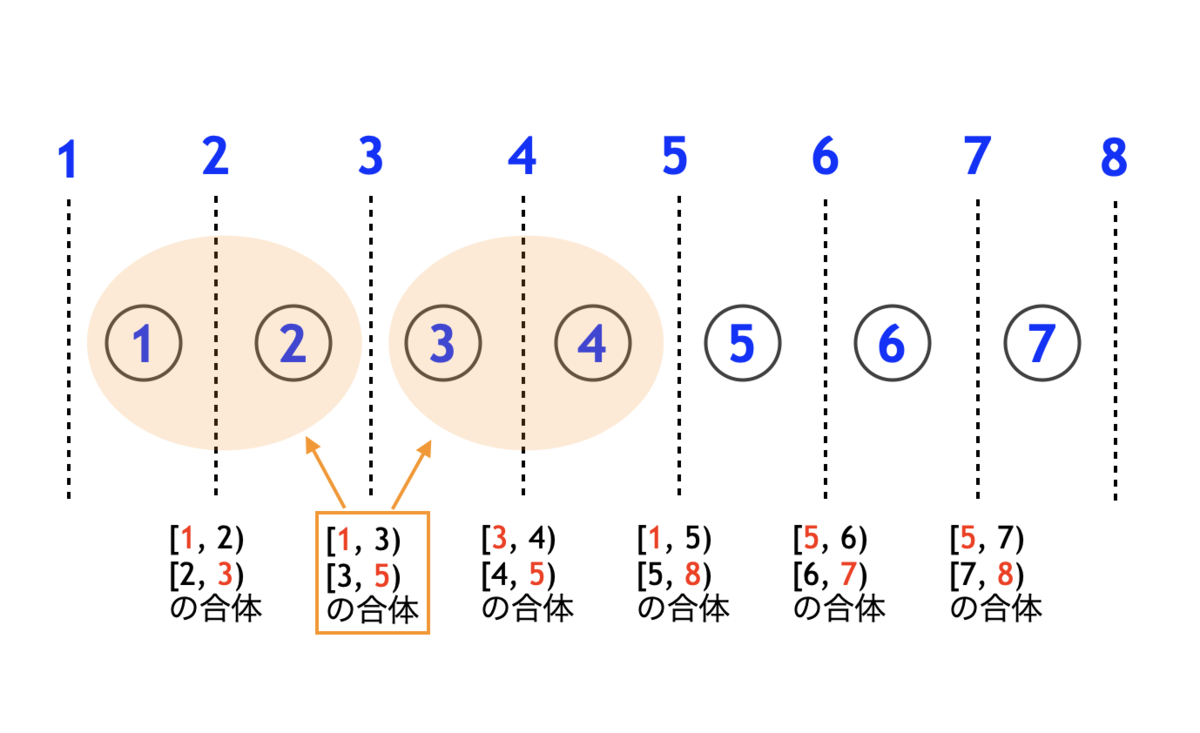
つまり、区間 [1, 2) と区間 [2, 3) から頂点を 1 個ずつ選んで辺を結び、区間 [1, 3) と区間 [3, 5) から頂点を 1 個ずつ選んで辺を結び......という順序で辺を結んでいっても良さそうだということだ。

ここで不安なのは「木でないものも生成されてしまうかもしれない」という点だった。しかしながら、それぞれの隙間に対して、その隙間をまたぐ辺は 1 本しか存在しないので、閉路が形成されることはないとわかった。

2 つの文字列を考慮

ここまで 1 つの文字列から作られる木について考えてきたが、ここから 2 つの文字列 $S, T$ から作られる木を考える。

とりあえず次の手続きで作られる木が条件を満たすことは簡単に言える。

【2 つの文字列から木を作る手続き】

各「頂点と頂点の隙間」に対して、
隙間の左側について、 $S$ 側についての区間と、 $T$ 側についての区間の共通区間に含まれる頂点を 1 個選ぶ
隙間の右側について、 $S$ 側についての区間と、 $T$ 側についての区間の共通区間に含まれる頂点を 1 個選ぶ
これらの 2 頂点を辺で結ぶ

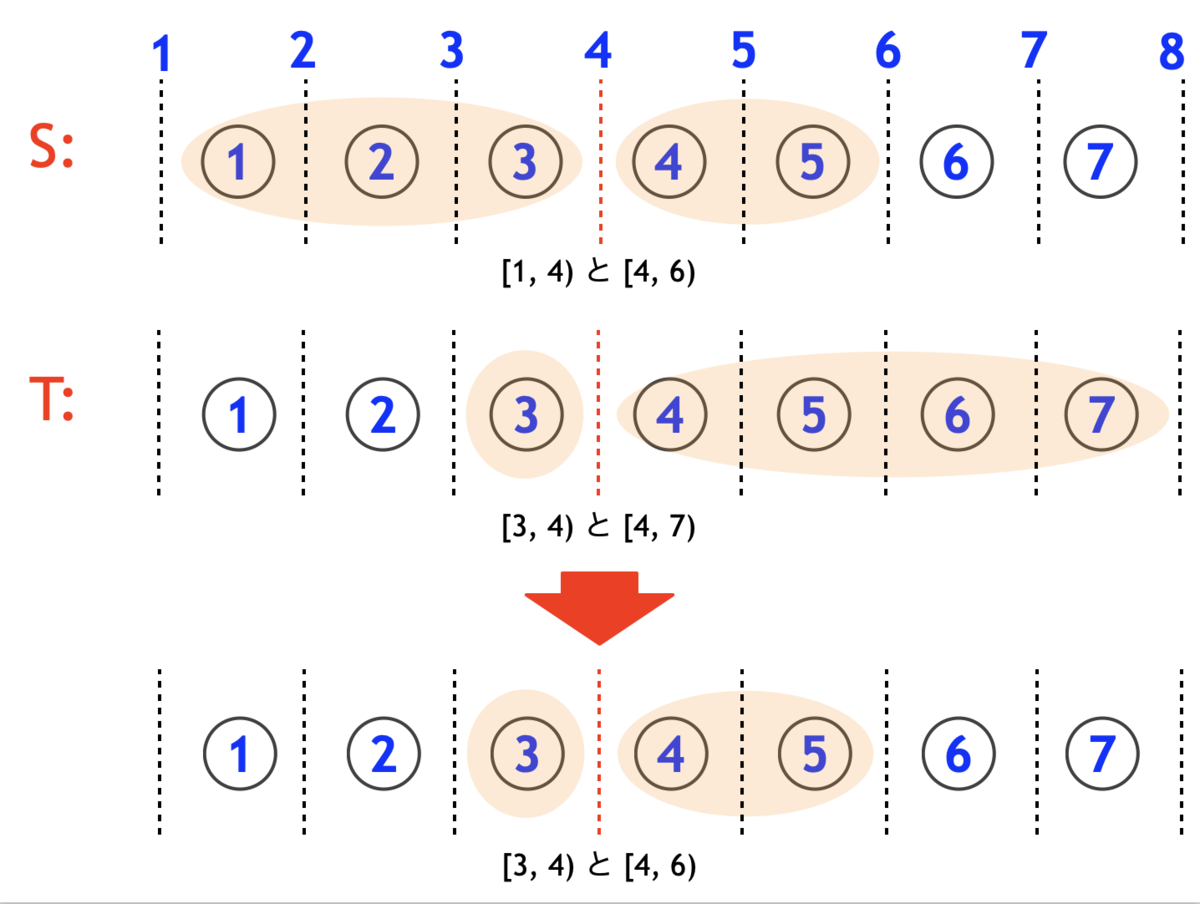
たとえば、上図のように、隙間 4 に対して、 $S$ 側の左側区間が [1, 4) で右側区間が [4, 6) であり、 $T$ 側の左側区間が [3, 4) で右側区間が [4, 8) であるとき、左右それぞれについて $S, T$ 両側で共通部分をとり、

「左側区間 [3, 4) から頂点を 1 つ選び、右側区間 [4, 6) から頂点を 1 つ選んで、これら 2 頂点を結ぶ」

とすればよい。

不安なのは、同じ隙間に対して $S, T$ 側で異なる頂点対を結ぶようなことがあったとしても、最終的に条件を満たす木になり得るのではないか......ということだった。しかし、これはありえない。なぜならば、すでに考察したように「同じ隙間をまたぐ辺は 1 本だけ」ということがわかっているからだ。

よって、上述の【2 つの文字列から木を作る手続き】によって作られる木の個数を数えれば良いことがわかった。

コード

文字列 $S$ が与えられたときに、各「頂点と頂点の隙間」に対して、左側の区間と右側の区間を求める部分は、スタックを用いて $O(|S|)$ の計算量で求められる。

よって、全体として $O(|S|)$ の計算量で答えが求められる。

#include <bits/stdc++.h>
using namespace std;
const int MOD = 998244353;

// 各隙間の左側区間の左端と、右側区間の右端を求めていく
pair<vector<long long>, vector<long long>> parse(const string &S) {
    vector<int> oneids;
    for (int i = 0; i < S.size(); i++) if (S[i] == '1') oneids.emplace_back(i);
    vector<long long> left(oneids.size(), -1), right(oneids.size(), -1);

    vector<pair<int,int>> stk;  // 頂点区間を格納するスタック
    for (int i = 0; i < S.size(); i++) {
        if (S[i] == '1') {
            int id = lower_bound(oneids.begin(), oneids.end(), i) - oneids.begin();
            stk.emplace_back(id, id + 1);  // 単独の頂点からなる区間をスタックに挿入
        } else if (S[i] == ')') {
            auto [m, r] = stk.back();  // 隙間 m の、左側区間
            stk.pop_back();
            auto [l, m2] = stk.back();  // 隙間 m の、右側の区間（m = m2 である）
            stk.pop_back();
            stk.emplace_back(l, r);
            left[m] = l, right[m] = r;  // 隙間 m の左側区間の左端は l、右側区間の右端は r
        }
    }
    return make_pair(left, right);
}

int main() {
    string S, T;
    cin >> S >> T;

    auto [ls, rs] = parse(S);
    auto [lt, rt] = parse(T);
    long long res = 1;
    for (long long i = 1; i < ls.size(); i++) {
        long long lnum = i - max(ls[i], lt[i]), rnum = min(rs[i], rt[i]) - i;
        long long mul = lnum * rnum % MOD;
        res = res * mul % MOD;
    }
    cout << res << endl;
}