AtCoder ARC 102 F - Revenge of BBuBBBlesort! (銅色, 1200 点)

メッチャ楽しい問題！！！

問題へのリンク

問題概要 (ARC 102 F)

1 〜 N の順列が与えられる。

• 連続する三要素が単調減少のとき、それをひっくり返す

という操作を好きなだけ行って、恒等順列にできるかどうか判定せよ。

制約

• 1 <= N <= 3 × 10⁵

解法 (全然わからなかった...)

(1, 2, ..., N) に「単調増加な連続三要素のひっくり返し」を繰り返して P を作れるかを判定する問題と考えてよい。

(i-1, i, i+1) に関する操作は swap(P[i-1], P[i+1]) である。これを「i を pivot とした swap」と呼ぶことにする。

まず、

• 隣接する二要素を pivot とした swap はできない

という重要な性質がある。証明は解説を参照に。そうすると、以下のように区間に分けることができる (公式解説放送より):

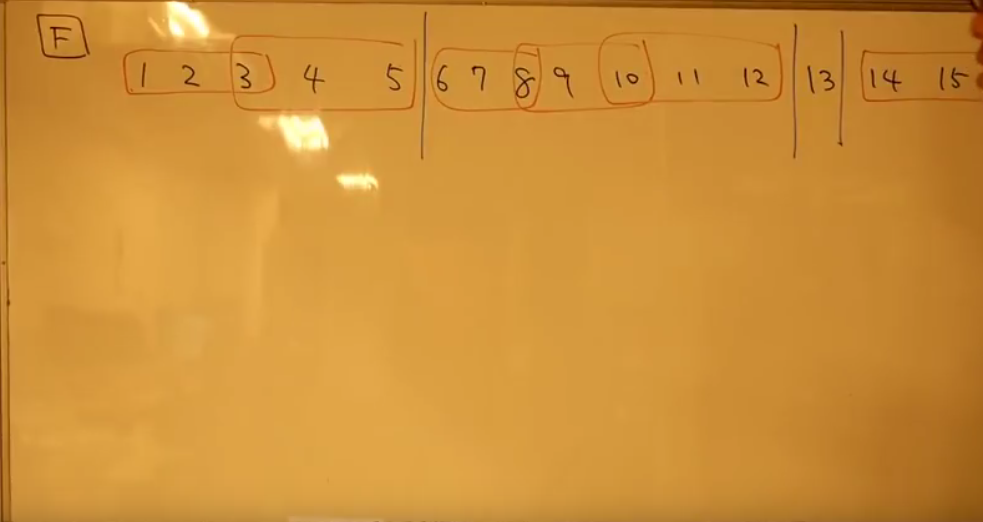
区間の区切れ目は

• P[i] = i が二回以上連続する箇所
• P[i] != i が二回以上連続する箇所

で区切って行けばいい。各区間ごとについて

• 初期状態から見て右に行く数字同士では相対的な位置関係が変わらない
• 初期状態から見て左に行く数字同士では相対的な位置関係が変わらない

という風になっている。逆に相対的な位置関係が変わらないなら、順列 P を実現できることを示せる。これを元に実装する。

#include <iostream>
#include <vector>
using namespace std;

int N;
vector<int> P;

bool solve() {
    vector<int> maxLeftP(N+1, 0), minRightP(N+1, N-1); // 左累積max、右累積min
    for (int i = 0; i < N; ++i) maxLeftP[i+1] = max(maxLeftP[i], P[i]);
    for (int i = N; i >= 1; --i) minRightP[i-1] = min(minRightP[i], P[i-1]);
    
    // 区間ごとに区切った時に、区間の外へと数字が逃げていかない条件
    // maxLeftP[i+1] = i は (1, 2, ..., i) の部分が最終的にその並び替えになっていることを意味する
    for (int i = 0; i < N-1; ++i) {
        // 連続して固定値のときはそこで途切れているはず
        if (P[i] == i && P[i+1] == i+1) { if (maxLeftP[i+1] != i) return false; }
        
        // 連続して固定値でないときは、i: 左へ行っているはず、i+1: 右へ行っているはず (つまり区切れる)
        if (P[i] != i && P[i+1] != i+1) { if (maxLeftP[i+1] != i) return false; }
    }
    
    for (int i = 1; i+1 < N; ++i) {
        // 増加している i は最後には右隣を pivot としているはずで、その場合はより大きい値が左には来れない
        if (P[i] > i) { if (maxLeftP[i] > P[i]) return false; }
        
        // 減少している i は最後には左隣を pivot としているはずで、その場合はより小さい値が右には来れない
        else if (P[i] < i) { if (minRightP[i] < P[i]) return false; }
    }

    return true;
}

int main() {
    cin >> N;
    P.resize(N);
    for (int i = 0; i < N; ++i) cin >> P[i], --P[i];
    if (solve()) cout << "Yes" << endl;
    else cout << "No" << endl;
}