2022-12-29

AtCoder ABC 282 E - Choose Two and Eat One (青色, 500 点)

これをグラフの問題だと思えるかどうか！

問題へのリンク

問題概要

箱の中に $N$ 個のボールが入っており、各ボールには $1$ 以上 $M−1$ 以下の整数が書かれている。 $i$ 番目のボールに書かれた整数は $A_{i}$ である。

箱の中に 2 個以上のボールが残っている限り、下記の行動を繰り返す。

箱の中から 2 つのボールを選んで取り出す
取り出した 2 つのボールに書かれた整数をそれぞれ $x,y$ としたとき、 $x^{y} + y^{x} \bmod M$ を得点として獲得する
その後、取り出した 2 つのボールのうち、片方を削除して、もう片方を箱に戻す

合計得点としてあり得る最大値を求めよ。

制約

$2 \le N \le 500$
$2 \le M \le 10^{9}$
$1 \le A_{i} \le M - 1$

考えたこと

まず最初に考えたことは「 $x^{y} + y^{x} \bmod M$ などという設定」はほとんど意味がないであろうということだった。本当は $N \times N$ の行列を与えて、ボール $x, y$ に対して操作する得点は $A_{x, y}$ であるというようにしてもいいくらいの感じだろうと思った。それだと入力が多くなるので、乱数っぽいものを用意したのだろうと。

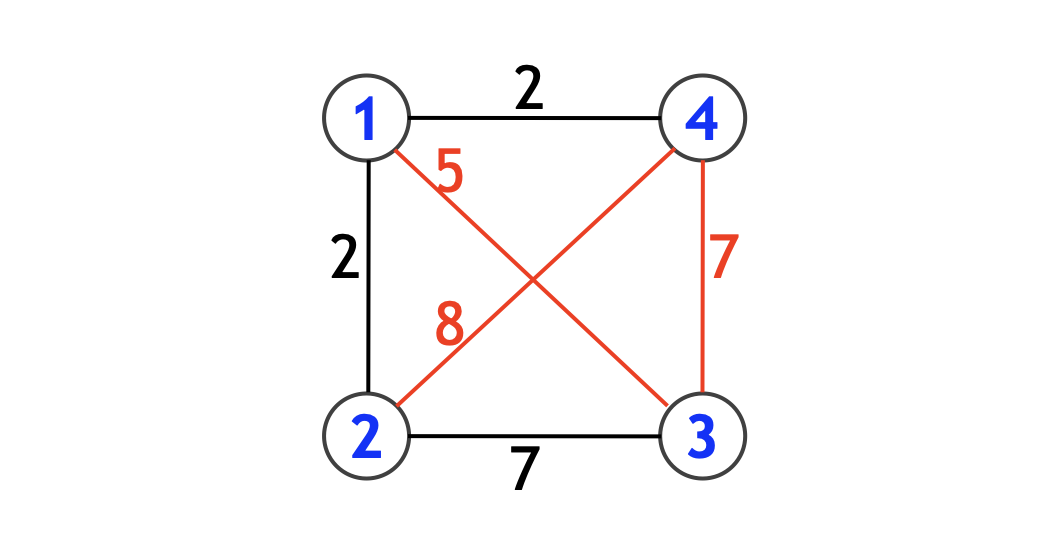
というわけで、サンプル 1 について、 $N \times N$ の表にしてみる。

	ボール 1	ボール 2	ボール 3	ボール 4
ボール 1	x	2	5	2
ボール 2	2	x	7	8
ボール 3	5	7	x	7
ボール 4	2	8	7	x

元の問題は、この表から $3$ 個の整数を選んだ総和が最大にするということになる。ただし、本当に大きい順に 3 つ選ぶことはできない。

この表の場合の最適解は (1, 3)、(2, 4)、(3, 4) である (ボール $x, y$ を選ぶことを $(x, y)$ と表記している)。

たとえば、(2, 3)、(2, 4)、(3, 4) とすれば、7 + 8 + 7 = 22 と大きくなるのに、それができないのはなぜだろうか？？　まず気づくのはボール 1 が登場していないこと。そして、下図のように、ボール 2, 3, 4 がループしてしまっていることだ。

ループしているとダメみたい。たとえば、ボール 2, 3 を選んでボール 3 を消したとする。次にボール 2, 4 を選んでボール 3 を消したとする。そしたら、ボール 4 だけが残るので、最後にボール 3, 4 を選ぶことはできない。

ボールを選ぶ順序や、消すボールをどっちにするかを、どのように選んでもダメだ。

グラフで考える

ここから先はグラフでちゃんと考えることにする。頂点数 $N$ の完全グラフだ。このグラフから $N-1$ 本の辺を選ぶ問題と言える (選んだ辺は「操作のために選ぶ 2 つのボールの組」に相当する)。

先ほどの観察から「選ぶ辺の集合によってループが形成されてはいけない」ということが言えそうだ。

実際これは容易に証明できる。もし $t$ 辺からなるループができたとする。このとき、どの順序で辺を選んだとしても、 $t-1$ 回目の作業を終えた時点で、 $t$ 個あったボールは残り 1 個になってしまう。最後の $t$ 回目の作業ができないのだ。

以上から、選ぶ辺集合がループを形成しないことが必要条件だと言えた。つまり、全域木になることが必要だということだ。

全域木ならすべて作れる

逆に、任意の全域木は、上手に「2 つのボールを選ぶ順序」と「どちらのボールを消すか」を設定することで実現できる。

具体的には、以下のことを繰り返せば良い。このように「葉から順に処理していく」という考え方はよく見かける。

まだ残っているボール (に対応する頂点) のうち、葉を 1 つ選ぶ
その葉に接続している辺の両端に対応する 2 つのボールを取り出す
葉に対応する側のボールを食べる

これを繰り返すことで、「取り出した 2 つのボールに対応する辺の集合」が所望の全域木になるようにすることができる。

最大全域木問題

以上より、この問題は「最大全域木問題」に帰着された。最小全域木問題は有名。それと同じ方法で最大全域木問題も解ける。つまり、Kruskal 法を辺が重い順に適用していけばよい。

Kruskal 法はたとえばけんちょん本では 15 章に書いた。

計算量は $O(N^{2} \log {N})$ となる。なお余談だが、Prim 法を priority_queue を用いずに書く方法で $O(N^{2})$ にすることもできる。

コード

#include <bits/stdc++.h>
using namespace std;
using pint = pair<int, int>;

// a^n mod m
long long modpow(long long a, long long n, long long mod) {
    long long res = 1;
    while (n > 0) {
        if (n & 1) res = res * a % mod;
        a = a * a % mod;
        n >>= 1;
    }
    return res;
}

// Union-Find
struct UnionFind {
    vector<int> par;

    UnionFind() { }
    UnionFind(int n) : par(n, -1) { }
    void init(int n) { par.assign(n, -1); }
    
    int root(int x) {
        if (par[x] < 0) return x;
        else return par[x] = root(par[x]);
    }
    
    bool issame(int x, int y) {
        return root(x) == root(y);
    }
    
    bool merge(int x, int y) {
        x = root(x); y = root(y);
        if (x == y) return false;
        if (par[x] > par[y]) swap(x, y); // merge technique
        par[x] += par[y];
        par[y] = x;
        return true;
    }
    
    int size(int x) {
        return -par[root(x)];
    }
};

using pint = pair<int,int>;  // 頂点対
using Edge = pair<long long, pint>;  // 重み付き辺

int main() {
    // 入力
    long long N, M;
    cin >> N >> M;
    vector<long long> A(N);
    for (int i = 0; i < N; ++i) cin >> A[i];

    // すべての辺を求めて、重い順にソート
    vector<Edge> edges;
    for (int i = 0; i < N; ++i) {
        for (int j = i+1; j < N; ++j) {
            long long cost = (modpow(A[i], A[j], M) + modpow(A[j], A[i], M)) % M;
            edges.push_back(Edge(cost, pint(i, j)));
        }
    }
    sort(edges.begin(), edges.end(), greater<Edge>());

    // Kruskal 法の適用
    long long res = 0;
    UnionFind uf(N);
    for (auto e : edges) {
        long long add = e.first;
        int u = e.second.first, v = e.second.second;
        if (uf.issame(u, v)) continue;
        res += add;
        uf.merge(u, v);
    }
    cout << res << endl;
}

けんちょんの競プロ精進記録

競プロの精進記録や小ネタを書いていきます