けんちょんの競プロ精進記録

競プロの精進記録や小ネタを書いていきます

Union-Find の中身のグループ分けを知る関数 groups() を実装する！

テーマ解説記事 Union-Find データ構造

多くの競プロerにとって、標準ライブラリ以外で自分の手で初めて実装するデータ構造は Union-Find でしょう。

自分でデータ構造を実装するとき、その中身がどうなっているかをきちんと把握できないと不安を感じてしまうこともあるでしょう。そこで本記事では、Union-Find のグループ構造がどうなっているかを詳しく知るための関数 groups() を実装してみます。

たとえば、下図のようなグループに対して、2 次元配列 {{0, 2, 4, 7}, {3, 5}, {6}} を返すようにします。

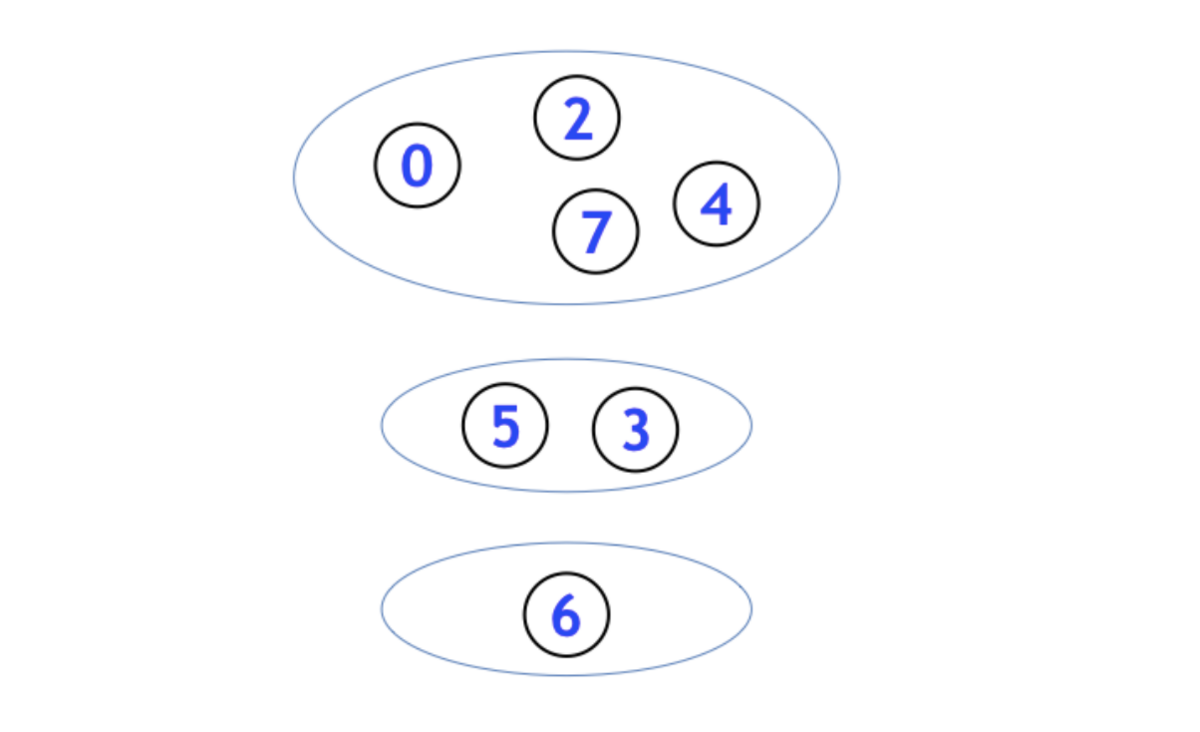
なお、ACL の Union-Find (dsu と呼ばれています) にも、グループ構造を知ることのできる groups() という関数があります。これを自分の手でも実装できるようにします。

　

目次

　

1. Union-Find の復習

Union-Find は、グループ分けを管理するデータ構造です。グループを併合したり、2 要素が同じグループに属するかどうかを判定したりできます。

Union-Find の関数 処理
unite(x, y) 要素 x を含むグループと要素 y を含むグループを併合する
same(x, y) 要素 x と要素 y が同じグループに含まれるかどうかを返す (true / false)

たとえば、下図のように、「0, 2, 4, 7」「3, 5」「6」という 3 つのグループがあるときに、unite(2, 3) を呼ぶと、要素 2 を含むグループ「0, 2, 4, 7」と要素 3 を含むグループ「3, 5」が併合されて、「0, 2, 3, 4, 5, 7」というグループになります。

　

　

Union-Find の仕組みの解説については他資料に譲りますが、一つだけ重要な補足として、各グループにはリーダーがいます。

Union-Find の各グループは「根付き木」で管理されています。この根頂点を、グループのリーダーとみなすことができるというわけです。グループを併合するときには、下図のように、どちらか一方のグループのリーダーが新グループのリーダーとなります。他方のグループのリーダーは、新たなリーダーの下につきます。

　

　

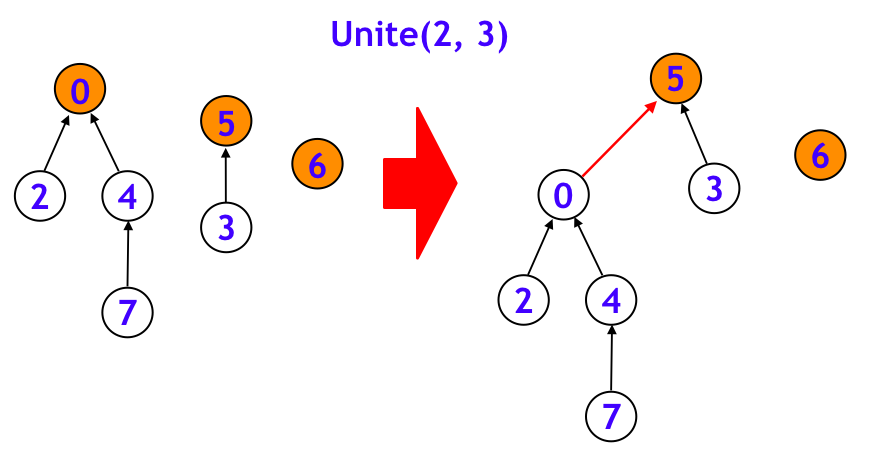
本記事では、要素 x のリーダーを取得する関数を root(x) とします。なお、ACL の Union-Find では根頂点を取得する関数 dsu::leader(v) が定義されています。

　

Union-Find の実装例の確認

ここで一度、Union-Find の実装を示します。関数

  • root(x)：要素 x のリーダー (根) を返す
  • unite(x, y)：要素 x, y を含むグループを併合する
  • same(x, y)：要素 x, y が同じグループに属するかを返す

をサポートしています。なお、このコードは Yosupo Judge - UnionFind に提出して AC になるものとなっています。

#include<bits/stdc++.h>
using namespace std;

// Union-Find
struct UnionFind {
    // core member
    vector<int> par;

    // constructor
    UnionFind() { }
    UnionFind(int n) : par(n, -1) { }
    void init(int n) { par.assign(n, -1); }
    
    // core methods
    int root(int x) {
        if (par[x] < 0) return x;
        else return par[x] = root(par[x]);
    }
    
    bool same(int x, int y) {
        return root(x) == root(y);
    }
    
    bool unite(int x, int y) {
        x = root(x), y = root(y);
        if (x == y) return false;
        if (par[x] > par[y]) swap(x, y); // merge technique
        par[x] += par[y];
        par[y] = x;
        return true;
    }
    
    int size(int x) {
        return -par[root(x)];
    }
};

int main() {
    int N, Q;
    cin >> N >> Q;
    UnionFind uf(N);
    for (int q = 0; q < Q; ++q) {
        int type, x, y;
        cin >> type >> x >> y;
        if (type == 0) uf.unite(x, y);
        else {
            if (uf.same(x, y)) cout << 1 << endl;
            else cout << 0 << endl;
        }
    }
}

　

2. Union-Find の関数 groups() の仕組み

それでは、いよいよ、Union-Find のグループ構造を取得する関数 groups() を実装します。前節で登場したリーダーの考え方を活用します。次の配列 member を用意しましょう。

vector<vector<int>> member：member[v] は要素 v をリーダーとするグループのメンバーを表す

この配列 member は次のように、各要素 v のリーダーを順に見ていくことで求められます ( N を要素数とします)。

vector<vector<int>> member(N);
for (int v = 0; v < N; ++v) {
    member[root(v)].push_back(v);
}

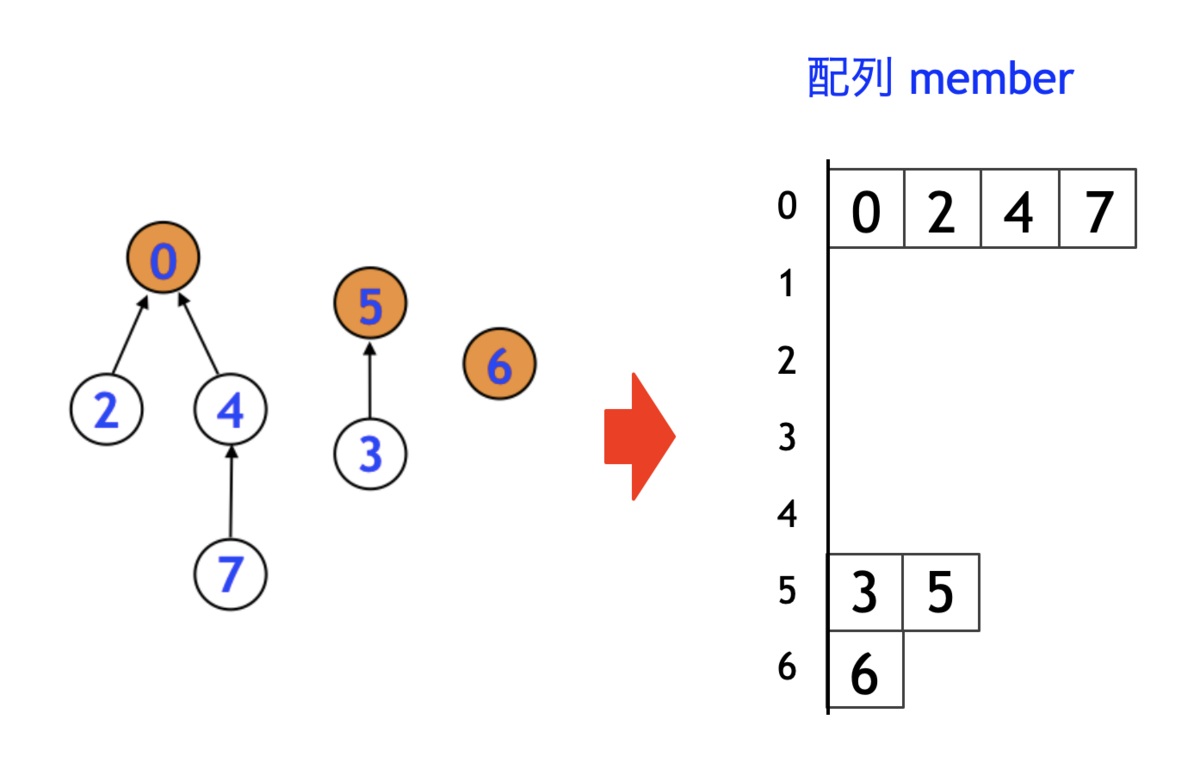
たとえば、上図の左側の Union-Find に対して配列 member を求めると右図のようになります。実は、すでにグループ分けができてることが見て取れます。残りは、配列の空の部分を削除するだけでグループ構造が取得できます。

この処理 groups() に要する計算量は O(N) となります。

一見、全要素の root を求めているので O(Nα(N)) の計算量となりそうです。しかし、経路圧縮の処理は、いわばメモ化再帰しているようなものですので、全要素の root を求める作業は O(N) の計算量と解析できます。

　

3. Union-Find の関数 groups() の実装

ここまでの話をまとめると、Union-Find のグループ分けの詳細を取得する関数 groups() は、次のコードのように実装できます。上のコード に対して、追加で関数 groups() を UnionFind のメンバ関数として実装しています。

#include<bits/stdc++.h>
using namespace std;

// Union-Find
struct UnionFind {
    // core member
    vector<int> par;

    // constructor
    UnionFind() { }
    UnionFind(int n) : par(n, -1) { }
    void init(int n) { par.assign(n, -1); }
    
    // core methods
    int root(int x) {
        if (par[x] < 0) return x;
        else return par[x] = root(par[x]);
    }
    
    bool same(int x, int y) {
        return root(x) == root(y);
    }
    
    bool unite(int x, int y) {
        x = root(x), y = root(y);
        if (x == y) return false;
        if (par[x] > par[y]) swap(x, y); // merge technique
        par[x] += par[y];
        par[y] = x;
        return true;
    }
    
    int size(int x) {
        return -par[root(x)];
    }
    
    // グループ構造の詳細を取得する関数
    vector<vector<int>> groups() {
        // member[v] := 要素 v をリーダーとするグループ
        vector<vector<int>> member(par.size());
        for (int v = 0; v < (int)par.size(); ++v) {
            member[root(v)].push_back(v);
        }
        
        // 配列 member の空の部分を削除したものを作る
        vector<vector<int>> res;
        for (int v = 0; v < (int)par.size(); ++v) {
            if (!member[v].empty()) res.push_back(member[v]);
        }
        return res;
    }
};

int main() {
    // グループ {{0, 2, 4, 7}, {1, 6}, {3, 5}} を作ってみる
    UnionFind uf(8);
    uf.unite(0, 2);
    uf.unite(2, 4);
    uf.unite(4, 7);
    uf.unite(3, 5);
    uf.unite(1, 6);
    
    // グループの詳細を取得
    vector<vector<int>> groups = uf.groups();
    
    // グループの詳細を出力
    for (vector<int> group : groups) {
        cout << "{";
        for (auto v : group) cout << v << " ";
        cout << "}" << endl;
    }
}

実行結果は次のようになります。確かにグループ構造を取得できました！！

{0 2 4 7 }
{1 6 }
{3 5 }

なお、ACL の Union-Find では、高速化のために「各グループのサイズを予め把握した上で、そのサイズの分だけ reserve() しておくことで、std::vector のメモリ再確保をしなくて済むようにする」などの工夫が行われています。とても見所満載なので、関心のある方は見てみるとよいでしょう！

　

4. おわりに

これで、Union-Find を使っていてバグったときなど、格段にデバッグしやすくなると思います！　これからもよき Union-Find ライフを！