「実は各点から左右に見て最も近い点だけ見れば良い」という点気考察をする！

問題へのリンク

問題概要

数直線上に $N$ 個の絵がある。 $i$ 番目の絵のある位置の座標は $A_{i}$ であり、'J', 'O', 'I', 'G' のいずれかの文字 $C_{i}$ が書かれている。

これらの絵に対して、以下の $Q$ 回のクエリに答えよ。

【クエリ】
2 つの座標 $s, t$ が与えられるので、以下の条件を満たす経路の移動距離の最小値を求めよ。

座標が $s$ である地点から、文字が 'J' であるいずれかの絵の位置に行く
その位置から、文字が 'O' であるいずれかの絵の位置に行く
その位置から、文字が 'I' であるいずれかの絵の位置に行く
その位置から、文字が 'G' であるいずれかの絵の位置に行く
その位置から、座標が $t$ である地点へ行く

制約

$4 \le N \le 10^{5}$
$1 \le Q \le 10^{5}$
各絵の座標や各クエリの $s, t$ の座標は 1 以上 $10^{15}$ 以下

考えたこと

経路を最適化する問題では、経路を単純化してもよいということがいえるかを考えるということが、とても有益だ。

今回の問題では、考えられる経路としてはまず、出発地点 $s$ から見て、 $s$ から到達できる J をすべて考えるのが確実だが、実は全てを考える必要はない。

たとえば、下図のように、 $s$ の左側に 2 個の J、右側に 2 個の J があるとしたとき、遠くの J は考える必要がない（考えてはいけないわけではない）。なぜなら、たとえ遠くの J に行くような経路が最適解であったとしても、「より近くの J を素通りするのではなく、一度その J を獲得してから、遠くの J を素通りすることにする」と考えても変わらないからだ。

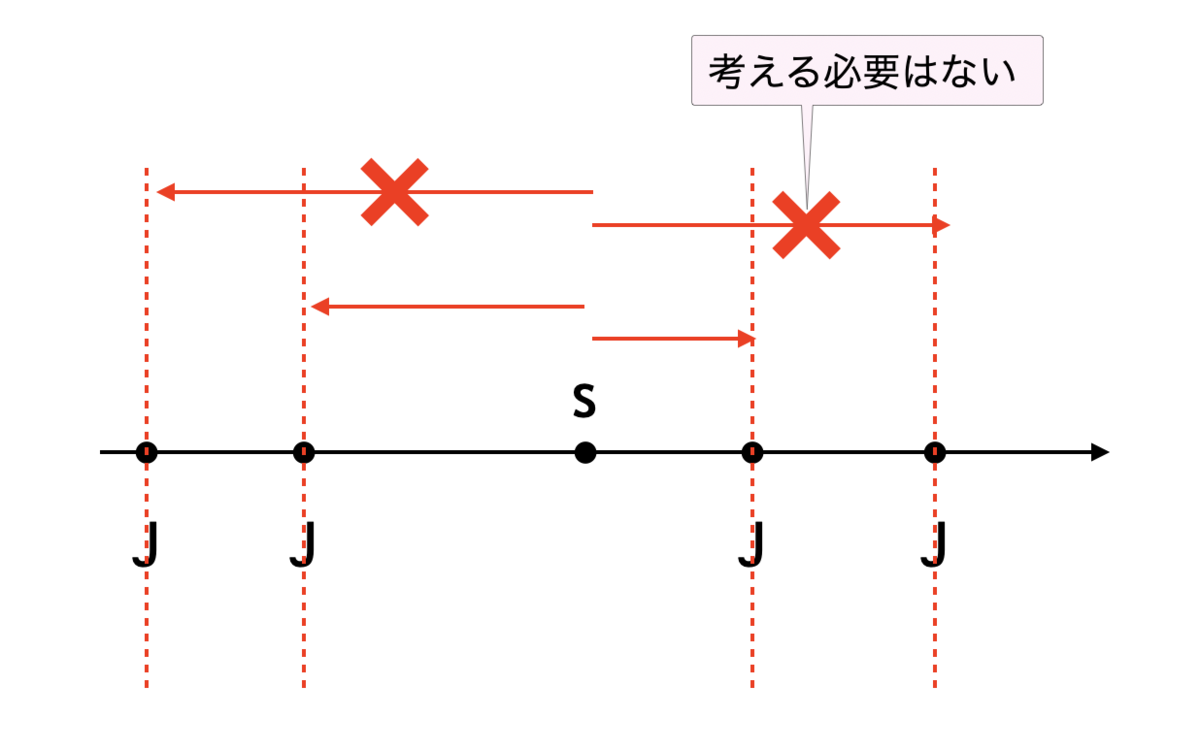
よって、調べるべき経路は、次の 16 通りに限られる（左右どちらかに存在しない場合はもっと減る）。

$s$ から、左側に最も近い J と、右側に最も近い J を調べる（2 通り）
その位置から、左側に最も近い O と、右側に最も近い O を調べる（2 通り）
その位置から、左側に最も近い I と、右側に最も近い I を調べる（2 通り）
その位置から、左側に最も近い G と、右側に最も近い G を調べる（2 通り）
その位置から、 $t$ へまっすぐ向かう

これら 16 通りの移動距離を求めて、その最小値を答えれば良い。

なお、「左側に最も近い J」や「右側に最も近い J」といったものは二分探索（C++ ならば関数 lower_bound()）を用いることで、 $O(\log N)$ の計算量で求められる。よって、1 回のクエリに答えるための計算量は $O(\log N)$ である（16 は定数であるため）。

以上より、全体の計算量は $O(N + Q \log N)$ となる。

コード

#include <bits/stdc++.h>
using namespace std;
const long long INF = 1LL<<55;

int main() {
    int N, Q;
    cin >> N;

    vector<vector<long long>> joig(4);
    for (int i = 0; i < N; i++) {
        long long x;
        char c;
        cin >> x >> c;
        if (c == 'J') joig[0].push_back(x);
        else if (c == 'O') joig[1].push_back(x);
        else if (c == 'I') joig[2].push_back(x);
        else joig[3].push_back(x);
    }
    for (int i = 0; i < 4; i++) {
        joig[i].push_back(-INF), joig[i].push_back(INF);
        sort(joig[i].begin(), joig[i].end());
    }

    cin >> Q;
    while (Q--) {
        long long s, t;
        cin >> s >> t;
        long long res = INF;
        for (int bit = 0; bit < (1 << 4); ++bit) {
            long long tmp = 0, cur = s;
            for (int i = 0; i < 4; ++i) {
                int it = lower_bound(joig[i].begin(), joig[i].end(), cur) - joig[i].begin();
                if (bit & (1 << i)) {
                    // left
                    tmp += abs(cur - joig[i][it - 1]);
                    cur = joig[i][it - 1];
                } else {
                    // right
                    tmp += abs(cur - joig[i][it]);
                    cur = joig[i][it];
                }
            }
            tmp += abs(cur - t);
            res = min(res, tmp);
        }
        cout << res << '\n';
    }
}

けんちょんの競プロ精進記録

競プロの精進記録や小ネタを書いていきます

JOIG 春合宿 2022 day1-2 JOIG ツアー (1Q, 難易度 7)

問題概要

制約

考えたこと

コード