キーエンス プログラミング コンテスト 2019 D - Double Landscape (青色, 500 点)

これ好き！！！本番中に通せれば

問題へのリンク

問題概要

のマス目に から までの数値を 個ずつ書きたい。 つの数列 と が与えられて

• 行目の最大値が
• 列目の最大値が

という性質を満たすものが何通りあるか、1000000007 で割ったあまりで求めよ。

制約

• 

考えたこと

とりあえず、数列 と は大きい順にソートしてしまって構わない。大きい方から考えた方が順々に決まって行きそうなので大きい方からソートする。

こういうのは手を動かして感触をつかむのが良さそう。手を動かして考えてみていると

• まずは の入る場所を考える。とりあえず でなきゃダメでそれ以外だとアウト。 のとき、(0, 0) マスが になる。

• 次に の入る場所を考える。 と のうちのどちらかが でなければアウト。

• ここで、下左図みたいに、 も も だと、(1, 1) が で確定する。

• 下右図みたいに、 が で が だと、(1, 0) が で確定して、 は黄色マスのうちのどちらかに入ることになる。

といったことが感じ取れる。さてとりあえず、こういう系の問題で思うこととして

• 各マスに何が入りうるのかを考える
• 各数字がどこのマスに入りうるのかを考える

という 2 つの方向性があるように思える (数独とかもそう) けど、今回は後者の視点が良さそうな気がしてくる。そこで状況をもう少し一般化して考えてみる。

はすでにどこかに入っているとして、 が入りそうなところを考える。また、A と B の より大きい値に関する条件はすでにすべてきちんと満たしていると仮定して考える。

A 側にも B 側にも x が登場するとき

下図のように、x が入る場所は一意に決まる。なお、x より大きい値はすべて、図の A 側の「x より大」と B 側の「x より大」のなす区域に入っているはずである。よって、

• A の x の行の x 以外のマスには x より小さい数しか入らない
• B の x の列の x 以外のマスには x より小さい数しか入らない

という条件を満たしているため、適合している。

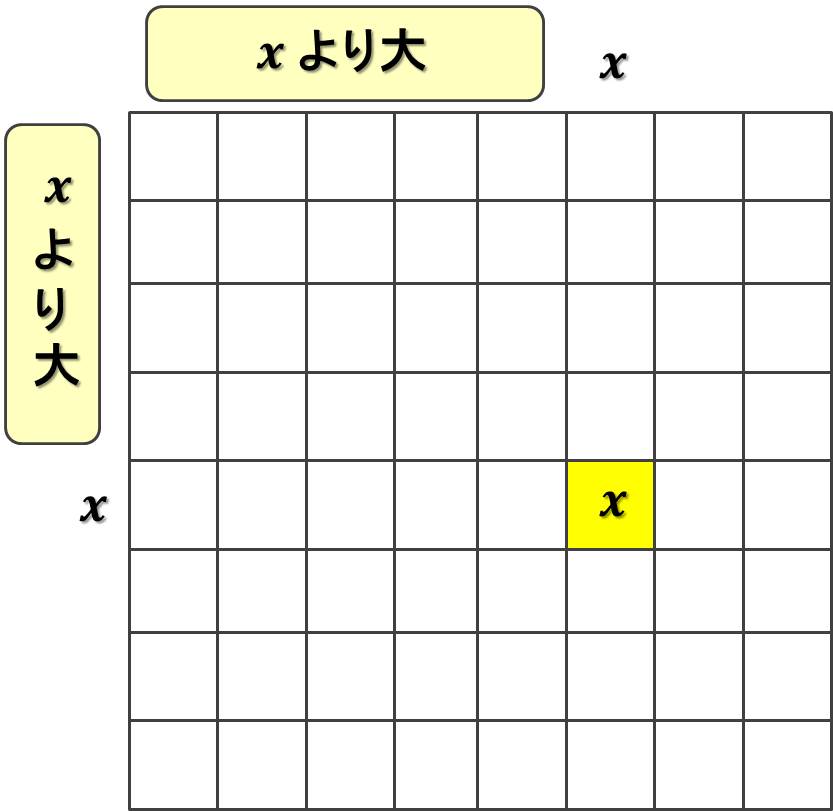
A 側にのみ x が登場するとき

下図のように、x が入る場所は B の「x より大きいところ」の個数分の黄マスのどこかに入ることになる。B の「x より小さいところ」にはみ出してしまうと、その列の最大値は x 以上となって矛盾する。

また、黄色マスには、x より大きい値が入ることはない。

よって、「B の x より大きい個数」通りの候補があり、x の行には x 以外のマスには x より小さい数しか入らないことが保証されるので、適合している。

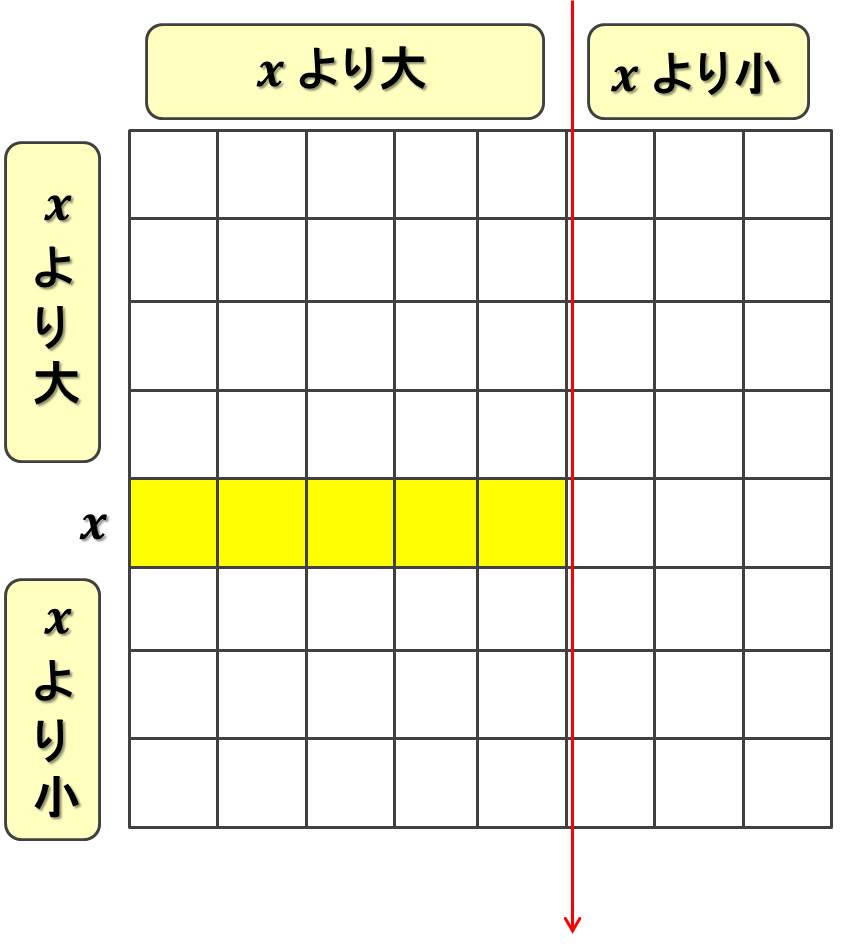
A 側にも B 側にも x が登場しないとき

x が入ることのできる場所は下図の黄色マスにかぎられる。ただし、黄色マスのうち、 個は よりも大きい値で埋められている ( より大きい値は黄色マス以外には入れないため)。

よって、「A の x より大きい個数」×「B の x より大きい個数」 - () 個の候補がある。

これが 以下になるとき、解なしである。

まとめ

以上の処理を とやって行けば OK。

#include <iostream>
#include <vector>
#include <algorithm>
using namespace std;

const int MOD = 1000000007;
int N, M;
vector<int> A, B;

long long solve() {
    long long res = 1;
    int biggerX_a = 0, biggerX_b = 0; // A, B で x より大きいのが何個あるか
    for (int x = N*M; x >= 1; --x) {
        if (A[biggerX_a] > x) return 0;
        if (B[biggerX_b] > x) return 0;
        
        long long tmp = 1;
        if (A[biggerX_a] == x && B[biggerX_b] == x) {
            tmp = 1;
            ++biggerX_a, ++biggerX_b;
        }
        else if (A[biggerX_a] == x) {
            tmp = biggerX_b;
            ++biggerX_a;
        }
        else if (B[biggerX_b] == x) {
            tmp = biggerX_a;
            ++biggerX_b;
        }
        else {
            tmp = biggerX_a * biggerX_b - (N * M - x);
            if (tmp <= 0) return 0;
        }
        res = (res * tmp) % MOD;
    }
    return res;
}

int main() {
    cin >> N >> M;
    A.resize(N + 1); B.resize(M + 1);
    for (int i = 0; i < N; ++i) cin >> A[i];
    for (int i = 0; i < M; ++i) cin >> B[i];
    sort(A.begin(), A.end(), greater<int>());
    sort(B.begin(), B.end(), greater<int>());
    cout << solve() << endl;
}