円と多角形の共通部分の面積を求めるライブラリ、一念発起して整備した!!!
サブルーチンとして「円と "線分" の交点を求める」というライブラリが必要となる。
問題概要
原点を中心とした半径 の円と、
頂点の多角形が与えられる。これらの共通部分の面積を求めよ (
以下の誤差を許容)。
ただし、多角形の頂点は反時計回りに与えられるものとする。
制約
- 各座標値の絶対値は
以下
考えたこと
円と多角形の共通部分の面積は、結局は
- 円 c
- 円 c の中心と、頂点 a と頂点 b を三頂点に持つ三角形
の共通部分の面積 (符号付き) を求める問題に帰着される。ここは not さんのツイートを引用。
こういうイメージなんですけど伝わってますか pic.twitter.com/eKE2d3GEHN
— not (@not_522) 2020年1月12日
これを頑張る。簡単のために、円 c の中心は原点であるとする (頂点 a, b を平行移動すれば OK)。さて、以下の 3 つの場合に分けて考える
- a も b も円 c に含まれるとき
- それ以外で線分 ab と円 c が交点を持たないとき
- 線分 ab と円 c が交点を持つとき
1. a も b も円 c に含まれるとき
このときは単純に、三角形 (原点, a, b) の面積を求める。この面積は符号付きで考える。
なお、このような三角形を (a, b) と書くことにする。
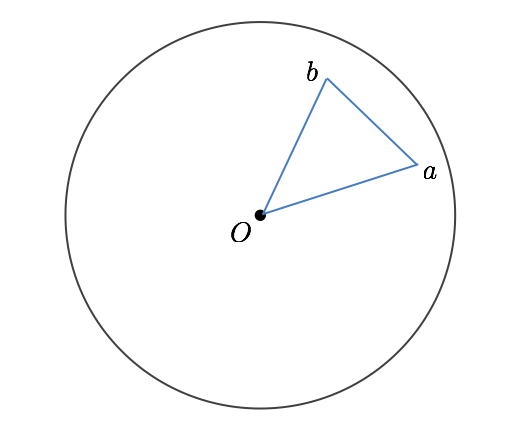
2. それ以外で線分 ab と円 c が交点を持たないとき
このときは、求める部分は「扇型の面積」になる。これも頑張る。三角形だけでなく、扇型の面積も符号付きで考える。点 a と b の偏角が逆だったら符号もマイナスになる。
なお、このような扇型を (a, b) と書くことにする。
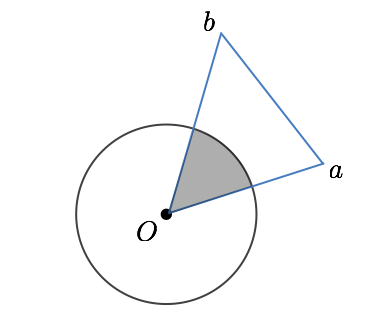
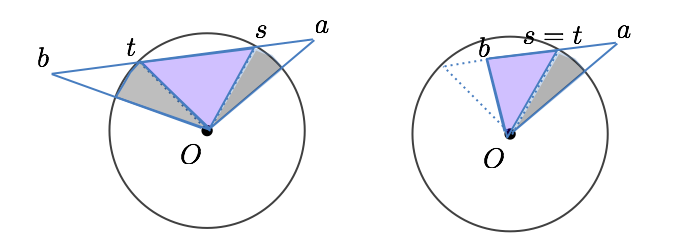
3. 線分 ab と円 c とが交点を持つとき
最後がちょっと大変。このときは丁寧に足し引きして求める。ここで「円と線分の交点」のライブラリが必要になる。
下図のような配置関係が考えられるが、これらは実は、符号付き面積を用いて統一的に扱える。以下を合計すれば OK
- 三角形 (s, t) の面積
- 三角形または扇型 (a, s) の面積 (a が円外なら扇型、円内なら三角形)
- 三角形または扇型 (t, b) の面積 (b が円外なら扇型、円内なら三角形)
注意点として、円 c と線分 ab との交点が複数あるとき、s は a に近い側になるようにする。
#include <iostream> #include <vector> #include <cmath> #include <iomanip> using namespace std; //////////////////////////// // 基本要素 (点, 線分, 円) //////////////////////////// using DD = long double; const DD INF = 1LL<<60; // to be set appropriately const DD EPS = 1e-6; // to be set appropriately const DD PI = acosl(-1.0); DD torad(int deg) {return (DD)(deg) * PI / 180;} DD todeg(DD ang) {return ang * 180 / PI;} /* Point */ struct Point { DD x, y; Point(DD x = 0.0, DD y = 0.0) : x(x), y(y) {} friend ostream& operator << (ostream &s, const Point &p) {return s << '(' << p.x << ", " << p.y << ')';} }; inline Point operator + (const Point &p, const Point &q) {return Point(p.x + q.x, p.y + q.y);} inline Point operator - (const Point &p, const Point &q) {return Point(p.x - q.x, p.y - q.y);} inline Point operator * (const Point &p, DD a) {return Point(p.x * a, p.y * a);} inline Point operator * (DD a, const Point &p) {return Point(a * p.x, a * p.y);} inline Point operator * (const Point &p, const Point &q) {return Point(p.x * q.x - p.y * q.y, p.x * q.y + p.y * q.x);} inline Point operator / (const Point &p, DD a) {return Point(p.x / a, p.y / a);} inline Point conj(const Point &p) {return Point(p.x, -p.y);} inline Point rot(const Point &p, DD ang) {return Point(cos(ang) * p.x - sin(ang) * p.y, sin(ang) * p.x + cos(ang) * p.y);} inline Point rot90(const Point &p) {return Point(-p.y, p.x);} inline DD cross(const Point &p, const Point &q) {return p.x * q.y - p.y * q.x;} inline DD dot(const Point &p, const Point &q) {return p.x * q.x + p.y * q.y;} inline DD norm(const Point &p) {return dot(p, p);} inline DD abs(const Point &p) {return sqrt(dot(p, p));} inline DD amp(const Point &p) {DD res = atan2(p.y, p.x); if (res < 0) res += PI*2; return res;} inline bool eq(const Point &p, const Point &q) {return abs(p - q) < EPS;} inline bool operator < (const Point &p, const Point &q) {return (abs(p.x - q.x) > EPS ? p.x < q.x : p.y < q.y);} inline bool operator > (const Point &p, const Point &q) {return (abs(p.x - q.x) > EPS ? p.x > q.x : p.y > q.y);} inline Point operator / (const Point &p, const Point &q) {return p * conj(q) / norm(q);} /* Line */ struct Line : vector<Point> { Line(Point a = Point(0.0, 0.0), Point b = Point(0.0, 0.0)) { this->push_back(a); this->push_back(b); } friend ostream& operator << (ostream &s, const Line &l) {return s << '{' << l[0] << ", " << l[1] << '}';} }; /* Circle */ struct Circle : Point { DD r; Circle(Point p = Point(0.0, 0.0), DD r = 0.0) : Point(p), r(r) {} friend ostream& operator << (ostream &s, const Circle &c) {return s << '(' << c.x << ", " << c.y << ", " << c.r << ')';} }; ////////////////////////////// // 円と線分の交点 ////////////////////////////// int ccw_for_crosspoint_cs(const Point &a, const Point &b, const Point &c) { if (cross(b-a, c-a) > EPS) return 1; if (cross(b-a, c-a) < -EPS) return -1; if (dot(b-a, c-a) < -EPS) return 2; if (norm(b-a) < norm(c-a) - EPS) return -2; return 0; } bool isinterPS_crosspoint_cs(const Point &p, const Line &s) { return (ccw_for_crosspoint_cs(s[0], s[1], p) == 0); } Point proj_for_crosspoint(const Point &p, const Line &l) { DD t = dot(p - l[0], l[1] - l[0]) / norm(l[1] - l[0]); return l[0] + (l[1] - l[0]) * t; } vector<Point> crosspoint_CS(const Circle &e, const Line &s) { vector<Point> res; Point p = proj_for_crosspoint(e, s); DD rcos = abs(e - p), rsin; if (rcos > e.r + EPS) return vector<Point>(); else if (e.r - rcos < EPS) rsin = 0; else rsin = sqrt(e.r * e.r - rcos * rcos); Point dir = (s[1] - s[0]) / abs(s[1] - s[0]); Point p1 = p - dir * rsin; Point p2 = p + dir * rsin; if (isinterPS_crosspoint_cs(p1, s)) res.push_back(p1); if (isinterPS_crosspoint_cs(p2, s) && !eq(p1, p2)) res.push_back(p2); return res; } ////////////////////////////// // 円と多角形の共通部分の面積 ////////////////////////////// // 原点, 点 x, 点 y とで囲まれる領域の面積 (三角形 ver と扇型 ver) DD calc_element(const Point &x, const Point &y, DD r, bool triangle) { if (triangle) return cross(x, y) / 2; else { Point tmp = y * Point(x.x, -x.y); DD ang = atan2(tmp.y, tmp.x); return r * r * ang / 2; } } // 円 C と、三角形 ((0, 0), ia, ib) との共通部分の面積 DD calc_common_area(const Circle &c, const Point &ia, const Point &ib) { Point a = ia - c, b = ib - c; if (abs(a - b) < EPS) return 0; bool isin_a = (abs(a) < c.r + EPS); bool isin_b = (abs(b) < c.r + EPS); if (isin_a && isin_b) return calc_element(a, b, c.r, true); Circle oc(Point(0, 0), c.r); Line seg(a, b); auto cr = crosspoint_CS(oc, seg); if (cr.empty()) return calc_element(a, b, c.r, false); auto s = cr[0], t = cr.back(); return calc_element(s, t, c.r, true) + calc_element(a, s, c.r, isin_a) + calc_element(t, b, c.r, isin_b); } // 円 c と多角形 pol の共通部分の面積 DD calc_common_area(const Circle &c, const vector<Point> &pol) { DD res = 0; int N = pol.size(); for (int i = 0; i < N; ++i) { res += calc_common_area(c, pol[i], pol[(i+1)%N]); } return res; } int main() { int N; DD r; cin >> N >> r; Circle c(Point(0, 0), r); vector<Point> pol(N); for (int i = 0; i < N; ++i) cin >> pol[i].x >> pol[i].y; cout << fixed << setprecision(10) << calc_common_area(c, pol) << endl; }